-
计算
- 求极限 lim n → ∞ ( 1 n 2 + 1 2 + 1 n 2 + 2 2 + ⋯ + 1 n 2 + n 2 ) \mathop{\lim }\limits_{n \to \infty } \left( \frac{1}{{\sqrt {n^2 + 1^2} }} + \frac{1}{{\sqrt {n^2 + 2^2} }} + \cdots + \frac{1}{{\sqrt {n^2 + n^2} }} \right) n→∞lim(n2+121+n2+221+⋯+n2+n21)。
- 求极限 lim x → 0 cos x − e − x 2 2 x 2 tan 2 x \mathop{\lim }\limits_{x \to 0} \frac{\cos x - e^{ - \frac{x^2}{2}}}{x^2 \tan^2 x} x→0limx2tan2xcosx−e−2x2。
- 设 f ( x ) = ∫ 1 x e − t 2 d t f(x) = \int_1^x e^{-t^2} \, \mathrm{d}t f(x)=∫1xe−t2dt,求 ∫ 0 1 x 2 f ( x ) d x \int_0^1 x^2 f(x) \, \mathrm{d}x ∫01x2f(x)dx。
- 设 u = x 2 + y 2 + z 2 u = x^2 + y^2 + z^2 u=x2+y2+z2, z = f ( x , y ) z = f(x,y) z=f(x,y) 且 x 2 + y 2 + z 2 = 3 x y z x^2 + y^2 + z^2 = 3xyz x2+y2+z2=3xyz,考虑使用隐函数,求 u x x u_{xx} uxx。
解答 1:
lim n → ∞ ( 1 n 2 + 1 2 + 1 n 2 + 2 2 + ⋯ + 1 n 2 + n 2 ) = lim n → ∞ 1 n ∑ k = 1 n 1 1 + ( k n ) 2 = ∫ 0 1 1 1 + x 2 d x = ∫ 0 π 4 sec t ( sec t + tan t ) sec t + tan t d t = ln ∣ sec t + tan t ∣ ∣ 0 π 4 = ln ( 2 + 1 ) \begin{align*} \mathop{\lim }\limits_{n \to \infty } \left( \frac{1}{{\sqrt{n^2 + 1^2}}} + \frac{1}{{\sqrt{n^2 + 2^2}}} + \cdots + \frac{1}{{\sqrt{n^2 + n^2}}} \right) &= \mathop{\lim }\limits_{n \to \infty } \frac{1}{n} \sum_{k = 1}^n \frac{1}{{\sqrt{1 + \left(\frac{k}{n}\right)^2}}} \\ &= \int_0^1 \frac{1}{{\sqrt{1 + x^2}}} \, \mathrm{d}x \\ &= \int_0^{\frac{\pi }{4}} \frac{\sec t \left(\sec t + \tan t\right)}{\sec t + \tan t} \, \mathrm{d}t \\ &= \ln \left| \sec t + \tan t \right| \bigg|_0^{\frac{\pi }{4}} \\ &= \ln \left( \sqrt{2} + 1 \right) \end{align*} n→∞lim(n2+121+n2+221+⋯+n2+n21)=n→∞limn1k=1∑n1+(nk)21=∫011+x21dx=∫04πsect+tantsect(sect+tant)dt=ln∣sect+tant∣ 04π=ln(2+1)
解答 2:
lim x → 0 cos x − e − x 2 2 x 2 tan 2 x = lim x → 0 cos x − e − x 2 2 x 4 = lim x → 0 ( 1 − x 2 2 ! + x 4 4 ! + o ( x 4 ) ) − ( 1 − x 2 2 + ( − x 2 2 ) 2 2 ! + o ( x 4 ) ) x 4 = lim x → 0 1 6 x 4 + o ( x 4 ) x 4 = 1 6 \begin{align*} \mathop{\lim }\limits_{x \to 0} \frac{\cos x - e^{ - \frac{x^2}{2}}}{x^2 \tan^2 x} &= \mathop{\lim }\limits_{x \to 0} \frac{\cos x - e^{ - \frac{x^2}{2}}}{x^4} \\ &= \mathop{\lim }\limits_{x \to 0} \frac{\left(1 - \frac{x^2}{2!} + \frac{x^4}{4!} + o(x^4)\right) - \left(1 - \frac{x^2}{2} + \frac{\left(- \frac{x^2}{2}\right)^2}{2!} + o(x^4)\right)}{x^4} \\ &= \mathop{\lim }\limits_{x \to 0} \frac{\frac{1}{6} x^4 + o(x^4)}{x^4} \\ &= \frac{1}{6} \\ \end{align*} x→0limx2tan2xcosx−e−2x2=x→0limx4cosx−e−2x2=x→0limx4(1−2!x2+4!x4+o(x4))−(1−2x2+2!(−2x2)2+o(x4))=x→0limx461x4+o(x4)=61
解答 3:
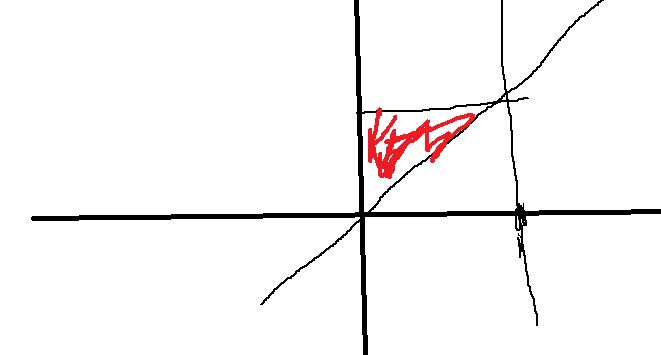
∫ 0 1 d x ∫ 1 x x 2 e − t 2 d t = − ∫ 0 1 d t ∫ 0 t x 2 e − t 2 d x = − ∫ 0 1 t 3 3 e − t 2 d t = − 1 6 ∫ 0 1 t 2 e − t 2 d ( t 2 ) = 1 6 ( t 2 e − t 2 + e − t 2 ) ∣ 0 1 = 1 3 e − 1 − 1 6 \begin{align*} \int_0^1 \mathrm{d}x \int_1^x x^2 e^{-t^2} \, \mathrm{d}t &= - \int_0^1 \mathrm{d}t \int_0^t x^2 e^{-t^2} \, \mathrm{d}x \\ &= - \int_0^1 \frac{t^3}{3} e^{-t^2} \, \mathrm{d}t \\ &= - \frac{1}{6} \int_0^1 t^2 e^{-t^2} \, \mathrm{d}(t^2) \\ &= \frac{1}{6} \left( t^2 e^{-t^2} + e^{-t^2} \right) \bigg|_0^1 \\ &= \frac{1}{3} e^{-1} - \frac{1}{6} \\ \end{align*} ∫01dx∫1xx2e−t2dt=−∫01dt∫0tx2e−t2dx=−∫013t3e−t2dt=−61∫01t2e−t2d(t2)=61(t2e−t2+e−t2) 01=31e−1−61
解答 4:
u x = 2 x + 2 z z x = 3 y z + 3 x y z x u_x = 2x + 2z z_x = 3yz + 3xy z_x ux=2x+2zzx=3yz+3xyzx
得到:
z x = 2 x − 3 y z 3 x y − 2 z z_x = \frac{2x - 3yz}{3xy - 2z} zx=3xy−2z2x−3yz
z x x = 2 + 2 z x 2 − 6 y z x 3 x y − 2 z = 1 ( 3 x y − 2 z ) 3 [ 2 ( 9 x 2 y 2 − 12 x y z + 4 z 2 ) + 2 ( 4 x 2 − 12 x y z + 9 y 2 z 2 ) − 6 ( 6 x 2 y 2 − 4 x z y − 9 x y 3 z + 6 y 2 z 2 ) ] = 1 ( 3 x y − 2 z ) 3 [ − 18 x 2 y 2 − 24 x y z + 8 z 2 + 8 x 2 − 18 y 2 z 2 + 54 x y 3 z ] \begin{align*} z_{xx} &= \frac{2 + 2 z_x^2 - 6y z_x}{3xy - 2z} \\ &= \frac{1}{\left(3xy - 2z\right)^3} \left [2\left(9x^2 y^2 - 12xyz + 4z^2\right) + 2\left(4x^2 - 12xyz + 9y^2 z^2\right) - 6\left(6x^2 y^2 - 4xzy - 9x y^3 z + 6y^2 z^2\right)\right] \\ &= \frac{1}{\left(3xy - 2z\right)^3} \left [-18x^2 y^2 - 24xyz + 8z^2 + 8x^2 - 18y^2 z^2 + 54x y^3 z\right] \end{align*} zxx=3xy−2z2+2zx2−6yzx=(3xy−2z)31[2(9x2y2−12xyz+4z2)+2(4x2−12xyz+9y2z
2023数学分析【南昌大学】
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.xdnf.cn/news/8404.html
如若内容造成侵权/违法违规/事实不符,请联系一条长河网进行投诉反馈,一经查实,立即删除!相关文章
从技术创新到商业应用,智象未来(HiDream.ai)创新不止步
在人工智能领域的最新动态中,智象未来(HiDream.ai)公司,作为全球领先的多模态生成式人工智能技术先驱,已经引起了广泛的行业瞩目。该公司专注于深度学习和计算机视觉技术的融合,致力于开发和优化视觉多模态…
ssm基于Vue的戏剧推广网站+vue
系统包含:源码论文
所用技术:SpringBootVueSSMMybatisMysql
免费提供给大家参考或者学习,获取源码看文章最下面
需要定制看文章最下面
目 录
摘 要 I
Abstract II
第1章 绪论 1
1.1 课题背景 1
1.2 课题意义 1
1.3 研究内容 1
第2…
利用泰勒公式近似计算10的平方根
文章目录 1. 泰勒公式是什么2、利用泰勒公式计算 10 \sqrt{10} 10 第 1 步:泰勒级数展开第 2 步:计算各阶导数第 3 步:在 x 9 x 9 x9 处计算各阶导数第 4 步:构建各阶泰勒展开式第 5 步:计算 f ( 10 ) f(10) f(1…
AI芯片:推动高性能计算场景的关键力量
大家好,我是Shelly,一个专注于输出AI工具和科技前沿内容的AI应用教练,体验过300款以上的AI应用工具。关注科技及大模型领域对社会的影响10年。关注我一起驾驭AI工具,拥抱AI时代的到来。
AI工具集1:大厂AI工具【共2…
C语言--结构体详解
一.前言 为了保证文章的质量和长度,小编将会分两篇介绍,思维导图如下,本文主要讲解概念部分,其中关于结构体内存对齐、位段等更加详细的内容将会在下一篇加以介绍,希望大家有所收获🌹🌹 在C语言…
完整教学:胡须图像分割
胡须图像分割系统源码&数据集分享
[yolov8-seg-act&yolov8-seg-C2f-Parc等50全套改进创新点发刊_一键训练教程_Web前端展示]
1.研究背景与意义
项目参考ILSVRC ImageNet Large Scale Visual Recognition Challenge
项目来源AAAI Global Al lnnovatio…
LeetCode 热题100 之 栈
1.有效的括号 思路分析:我们可以使用栈(stack)来解决这个问题。栈是一种先进后出的数据结构,这与括号匹配的需求非常契合。
unordered_map<char, char> bracket_map:这个哈希表用来存储右括号与左括号的对应关系…
git clone,用https还是ssh
前言 在使用Git去克隆项目时,会遇到https和ssh等形式,这两种又有何种区别呢,本文将重点讨论在具体使用中的问题。 注:第一次使用Git 时,需要先设置全局用户名和邮箱,否则后续使用命令时会报错,也是提醒先添…
【深圳大学/大学物理实验2】霍尔效应及其应用实验预习参考
霍尔效应及其应用 总分:100 组卷人:系统管理员成绩:95 一、单选题 共 10 小题 共 50 分 1. (5分)测量霍尔电压的原理公式是: 学生答案:C √ A. B. C. D. 2. (5分)载流子浓度n的计算式…
[全网最完整最详细C++篇]第四篇:类和对象(上)
目录 1->面向过程和面向对象初步认识
2->类的引入
3->类的定义
4->类的访问限定符及封装
4.1 访问限定符 4.2封装
5->类的作用域
6->类的实例化
7->类的对象大小的计算
7.1 如何计算类对象的大小
7.2 类对象的存储方式猜测
7.3 结构体内存对齐规…
Linux 服务器使用指南:从入门到登录
🌟快来参与讨论💬,点赞👍、收藏⭐、分享📤,共创活力社区。 🌟 🚩博主致力于用通俗易懂且不失专业性的文字,讲解计算机领域那些看似枯燥的知识点🚩 目录
一…
Netty篇(核心组件 - Channel)
目录 一、简介
二、ChannelFuture
三、CloseFuture
四、💡 异步提升的是什么 一、简介
channel 的主要作用
close() 可以用来关闭 channelcloseFuture() 用来处理 channel 的关闭 sync 方法作用是同步等待 channel 关闭而 addListener 方法是异步等待 channel …
JavaScript void 运算符
void定义:
void 运算符对给定的表达式进行求值,然后返回undefined。void是一个一元运算符,接受单个操作数,可以是任何类型,返回一个 undefined。
void语法:
void 在表达式的左边,void 右边的…
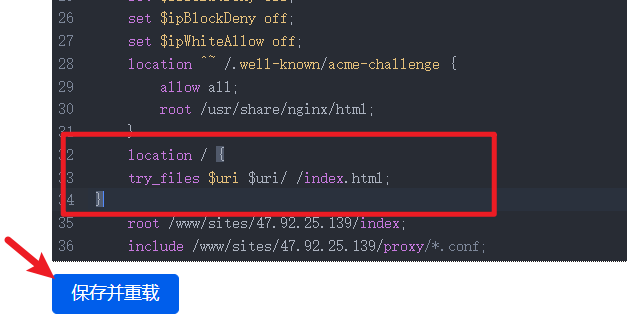
Vue+Springboot 前后端分离的项目如何部署?
本文转载自:https://fangcaicoding.cn/course/11/58 大家好!我是方才,目前是8人后端研发团队的负责人,拥有6年后端经验&3年团队管理经验,截止目前面试过近200位候选人,主导过单表上10亿、累计上100亿数…
sls日志服务采集json格式日志
springboot统计的json数据 1. 配置 Logback 输出 JSON 格式日志1.1添加依赖:1.2配置 Logback 输出日志: 2. 使用 LinkedHashMap 日志数据3. 将日志推送到 SLS4. 在阿里云 SLS 中查看日志5.补充:关于 JSON 格式输出5.补充:关于 JSO…
Python | Leetcode Python题解之第538题把二叉搜索树转换为累加树
题目: 题解:
class Solution:def convertBST(self, root: TreeNode) -> TreeNode:def getSuccessor(node: TreeNode) -> TreeNode:succ node.rightwhile succ.left and succ.left ! node:succ succ.leftreturn succtotal 0node rootwhile nod…
天命人开店日记之选址考察(上)
本次开店的品类是老年用品,前期与合作伙伴交流,按照新的线上与线下结合方式销售老年代步车和智能电动轮椅,线上占据70%销量,线下占据30%。线下门店可作为一个体验中心,对于本区域内的用户可以到线下门店体验࿰…








![[全网最完整最详细C++篇]第四篇:类和对象(上)](https://i-blog.csdnimg.cn/direct/57606650cd194c7b8b6d8a9400a112b0.jpeg)