由上一篇文章《Easy》中提到过的：

---

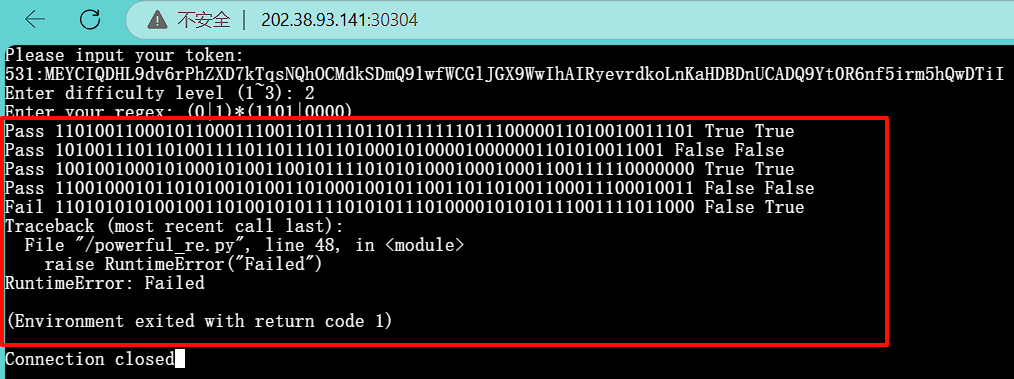
还是直接让AI写个python脚本生成难度2的正则表达式，但是生成的正则表达式无法成功获取到flag：

---

这里了解了一下相关知识，字符串形式的整数对常数求模是可以用有限状态机来实现的。对于二进制数字来讲，在末尾加上 0 相当于将数字乘以 2；在末尾加上 1 相当于将数字乘以 2 再加上 1。

---

假设状态编号 n 表示「现在的数字为 k % 13 = n」。在状态 n 时每次读到下一个字符时会有两种状态转移：

读到 0 时，在末尾加上 0 之后的数字 k' = 2k

新的状态为 k' % 13 = 2n % 13

读到 1 时，在末尾加上 1 之后的数字 k' = 2k + 1

新的状态为 k' % 13 = (2n + 1) % 13

这个自动机在开始匹配时的状态为 0。在自动机运行完之后，如果处在状态 n，则说明这个二进制数字除 13 余 n。

---

构建了这个状态机之后，就需要将它转化为正则表达式。我们需要匹配可以被 13 整除的二进制数字，因此起始状态和终止状态都为 0。

状态机转化到正则表达式的思想是一个个删除中间的状态（起始状态和终止状态之外的状态），最后将状态机转化为只有一个状态。删除中间的状态 q 时，我们需要将所有经过状态 q 的路径拼接起来。例如如果有 p -> q -> r 这样一条路径，则需要将 p -> q 和 q -> r 的状态转移拼接起来，得到一条 p -> r 的状态转移。

---

这里以「匹配 4 的倍数」的状态机举例：

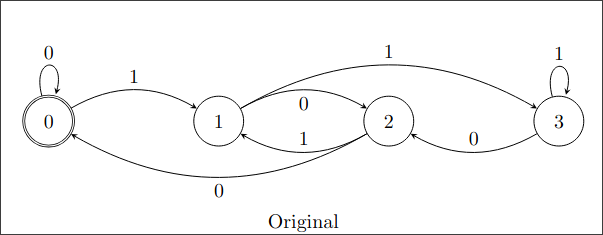
（具体数字可以看下面表格，圈内数字是状态）

读上标部分：

读到 0 时，在末尾加上 0 之后的数字 k' = 2k

新的状态为 k' % 4 = 2n % 4

读到 1 时，在末尾加上 1 之后的数字 k' = 2k + 1

新的状态为 k' % 4 = (2n + 1) % 4

状态k（n）	读上标数字（0,1）	状态k'
0	0	0【（2*0）%4=0】
0	1	1【（2*0+1）%4=1】
1	0	2【（2*1）%4=2】
1	1	3【（2*1+1）%4=3】
2	0	0【（2*2）%4=0】
2	1	1【（2*2+1）%4=1】
3	0	2【（2*3）%4=2】
3	1	3【（2*3+1）%4=3】

---

删掉状态3：

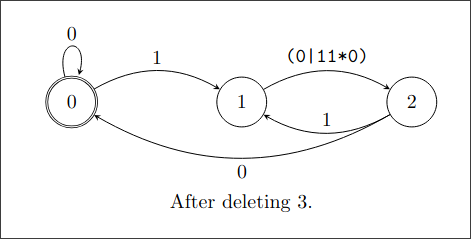
(0|11*0)

---

删掉状态2：

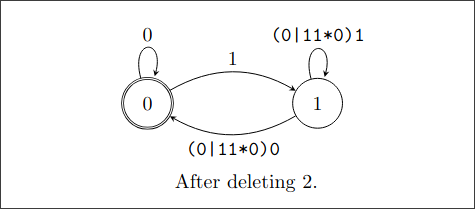
(0|11*0)1

(0|11*0)0

---

删掉状态1：

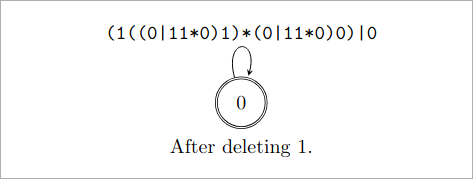
(1((0|11*0)1)*(0|11*0)0)|0

---

「匹配 13 的倍数」的状态机也是同理，编写python代码：

# 定义状态数量
n = 13# 初始化状态转移矩阵，每个元素是一个列表，用于存储可能的转移路径
paths = [[[] for _ in range(n)] for _ in range(n)]# 构建状态转移矩阵
for i in range(n):# 从状态 i 读入 0 后转移到状态 (2*i) % npaths[i][(2 * i) % n].append("0")# 从状态 i 读入 1 后转移到状态 (2*i+1) % npaths[i][(2 * i + 1) % n].append("1")# 定义一个函数，用于将多个路径合并成一个正则表达式
def path_union(lst):return "(" + "|".join(lst) + ")"# 当前状态数量
state_count = n# 逐步消除状态，直到只剩下一个状态
while state_count > 1:target = state_count - 1  # 当前要消除的状态loop = ""  # 用于存储目标状态到自身的循环路径# 如果目标状态有自环路径，构建自环正则表达式if len(paths[target][target]) > 0:loop = path_union(paths[target][target]) + "*"# 消除目标状态后，更新其他状态之间的路径for i in range(target):for j in range(target):if len(paths[i][target]) > 0 and len(paths[target][j]) > 0:# 从状态 i 到状态 j 的新路径 = 从 i 到 target 的路径 + 自环路径 + 从 target 到 j 的路径new_path = path_union(paths[i][target]) + loop + path_union(paths[target][j])paths[i][j].append(new_path)# 减少状态数量state_count -= 1# 最终生成的正则表达式是从状态 0 出发并回到状态 0 的所有路径的并集
regex = path_union(paths[0][0]) + "*"# 打印生成的正则表达式
print(f"生成的正则表达式为: {regex}")

但这个正则表达式明显过长了，换一种思路，直接用网络连接来传输生成的正则表达式

---

加上网络连接部分对应的python代码：

import pwn# 令牌
token = b"531:MEYCIQDHL9dv6rPhZXD7kTqsNQhOCMdkSDmQ9lwfWCGlJGX9WwIhAIRyevrdkoLnKaHDBDnUCADQ9Yt0R6nf5irm5hQwDTiI"# 建立远程连接
conn = pwn.remote('202.38.93.141', 30303)# 发送令牌
conn.send(token)
conn.send(b"\n")# 接收提示信息
conn.recvuntil(b"(1~3): ")# 选择选项2
conn.send(b"2\n")# 接收提示信息
conn.recvuntil(b"regex: ")# 定义状态数量
n = 13# 初始化状态转移矩阵，每个元素是一个列表，用于存储可能的转移路径
paths = [[[] for _ in range(n)] for _ in range(n)]# 构建状态转移矩阵
for i in range(n):# 从状态 i 读入 0 后转移到状态 (2*i) % npaths[i][(2 * i) % n].append("0")# 从状态 i 读入 1 后转移到状态 (2*i+1) % npaths[i][(2 * i + 1) % n].append("1")# 定义一个函数，用于将多个路径合并成一个正则表达式
def path_union(lst):return "(" + "|".join(lst) + ")"# 当前状态数量
state_count = n# 逐步消除状态，直到只剩下一个状态
while state_count > 1:target = state_count - 1  # 当前要消除的状态loop = ""  # 用于存储目标状态到自身的循环路径# 如果目标状态有自环路径，构建自环正则表达式if len(paths[target][target]) > 0:loop = path_union(paths[target][target]) + "*"# 消除目标状态后，更新其他状态之间的路径for i in range(target):for j in range(target):if len(paths[i][target]) > 0 and len(paths[target][j]) > 0:# 从状态 i 到状态 j 的新路径 = 从 i 到 target 的路径 + 自环路径 + 从 target 到 j 的路径new_path = path_union(paths[i][target]) + loop + path_union(paths[target][j])paths[i][j].append(new_path)# 减少状态数量state_count -= 1# 最终生成的正则表达式是从状态 0 出发并回到状态 0 的所有路径的并集
regex = path_union(paths[0][0]) + "*"# 打印生成的正则表达式
#print(f"生成的正则表达式为: {regex}")# 发送生成的正则表达式
conn.send(regex.encode())
conn.send(b"\n")# 进入交互模式
conn.interactive()

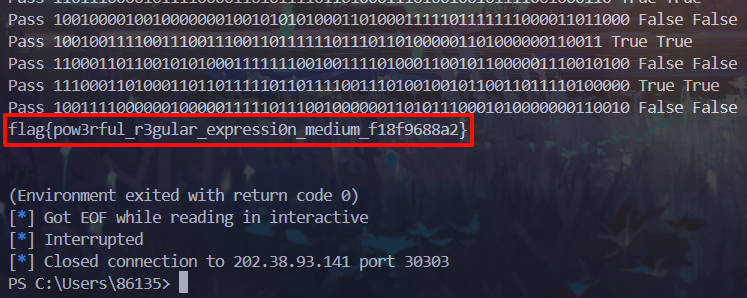
成功获取到flag