第一讲行列式的计算

基础定义和规则

ps：

交换时不止行可以交换，列方便时也可以

我的第一作法：是把行相加，然后后续无差别

范德蒙行列式的计算：

要求第一行/列全为1

每个公比元素作差再相乘

爪型

步骤：主对角线2-n个提公因子化为1，然后行列变换，借助三角行列式

余子式和代数余子式

行列式展开定理——借助代数余子式

尽量找0多一点的行或列

求数个代数余子式的和

因为代数余子式决定了与该行列对于的值无关，计算时并不会代入，直接用系数代替，计算代替后的行列的值，即为上述代数余子式之和的答案

求余子式之和同理：把余子式按照正负关系，转化为代数余子式即可

拆解

拉普拉斯公式——借助三角，注意是主对角线，副对角线记得互换行/列

第二讲：矩阵

定律

抽象矩阵求逆矩阵

方法2：直接除法，缺什么就乘什么，再补什么即可

分块矩阵求逆

数字型矩阵求逆、对应坐标

借助E

向量在基下的坐标，借助E

二阶速求：两调一除

——主交换，副*（-1），再除以绝对值

求解矩阵方程

矩阵换行不变号

求解简便方法，借助E

直接两个矩阵并列，把左边边化成E，右边即是答案

伴随矩阵

什么是方阵 什么是行列式

方阵行列式常用规律

借助A*的例题

矩阵的秩

第三讲：向量组的线性相关性

向量组去掉一个向量以后仍然无关

数字型向量组的相关性

含有0向量，必相关

若相关：对于模为0。或者秩<未知数的数量

抽象型

分别把向量组系数化为行列式，若行列式为0，则相关（模为0）

秩和极大无关组

极大无关组取阶梯型拐弯处的列向量，而基础解系取非拐弯处

第四讲：线性方程组

齐次求解，看只秩和未知数

当秩==未知数数量，有唯一的解（0解）

基础解系（无穷解情况下）

个数=自由变量个数

基础解系求法

最简形

拐口110类似，单位数字

将系数阵化为最简，记得取反

简单操作：直接根据最简方阵，若自由变量为x3、x4.取三四列数字的相反数，剩下两位分别对于个数为1，另一位为0

练习

详解：然后再转化为方程组，按基础解系个数设置新的未知数，把x（被原本未知数组成的）用新的代替，再把新未知数提出来，所带方阵即为基础解系

有几个未知数，自由变量就有几行

非齐次求解

！！！写增广矩阵就可以看出来——变阶梯型——再变行最简，注意行也要最简，怎么最简怎么处理

=齐通+非齐特

系数阵的秩==增广阵的秩==未知数数量，唯一；<未知数数量，无穷。两个秩不相等，无解

b为非齐次方程的非齐次数值部分

选择题 解之间的关系

求非奇特的过程

取增广阵右边，剩余取0即可

本身数值就在=右边，因此不需要取相反数

例题讲解

根据增广阵画出最简，然后再确定自由变量个数，直接读取解

切记！！！解方程组只能做行变换，不能做列的

带参数的方程组求解

非奇特就取右边的

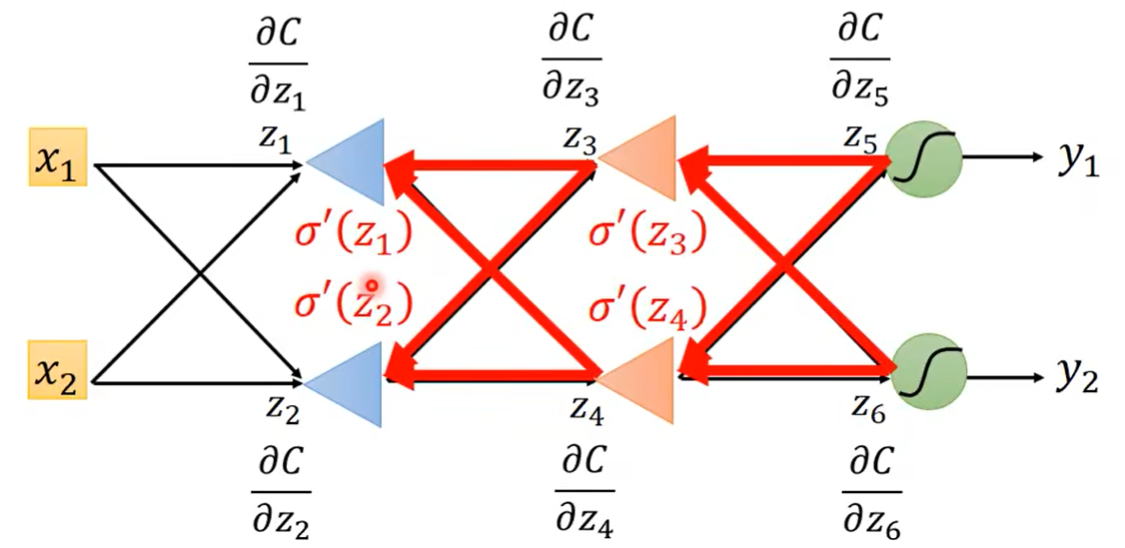
第五讲：矩阵的特征值和特征向量

一下方法都是先求特征值。特征向量，搭配基础解系

——特征值与特征向量的求法，特征向量就是基础解系

数字型

抽象型

——矩阵相关，特征值也相关

抽象型的模==特征值的乘积

矩阵的相似对角化（求可逆阵）

对角阵：主对角线为非0，其他为0

消去非 冷木大 的元素，若有公因子则是成功的

上述矩阵不是对称的

对称的要求正交矩阵

求正交阵的方法

上述特征求法，然后同个特征值的大概率不正交，就要化为正交的，然后除以自己的模单位化，形成正交阵，后续一串的主对角线即为特征值

特征向量不正交的要正交化，正交（其中一个变量的转置*另一个为0）

正交阵：每两列之间都是相互正交的

单位化：每个向量除以自己的摸

AT=A 为矩阵是对称的

第六讲：二次型

表示

其他元素找变量角标，角标原本和颠倒即为对应的位置

标准型

：只有二次项的，没有一次项

配方法

当不能直接看出来的配方，即可用下面的：一个一个未知数进行配方

正交法

最后替换y的系数为对于 冷木大 的

找基础解系时，记得判断当前要不要取相反数

同一个特征值演化出来的特征向量，往往不是正交的

直接把方程用y来代替，对应系数为对应的 冷木大 的值

正定矩阵

正惯性指数：标准型中正平方项未知数的个数

一般算各阶矩阵>0