文章目录
- 反向传播Backpropagation
- (1)Chain Rule
- (2)Forward pass和Backward pass
反向传播Backpropagation
对于计算Gradient Descent这件事情,我们的neural network是有非常非常多的参数,可能有上百万个参数。所以input的 θ \theta θ向量是有上百万维的。现在最大的困难就是,你要如何有效地去把这个百万维的向量计算出来。——这个就是Backpropagation在做的事情。

所以,Backpropagation并不是一个和Gradient Descent不同的训练方法,它本身就是Gradient Descent,它只是一个比较有效率的算法,让你在计算gradient这个向量的时候是比较有效率的。
(1)Chain Rule
Backpropagation里面没有特别高深的数学,你唯一需要记得的就是Chain Rule。(链式法则)
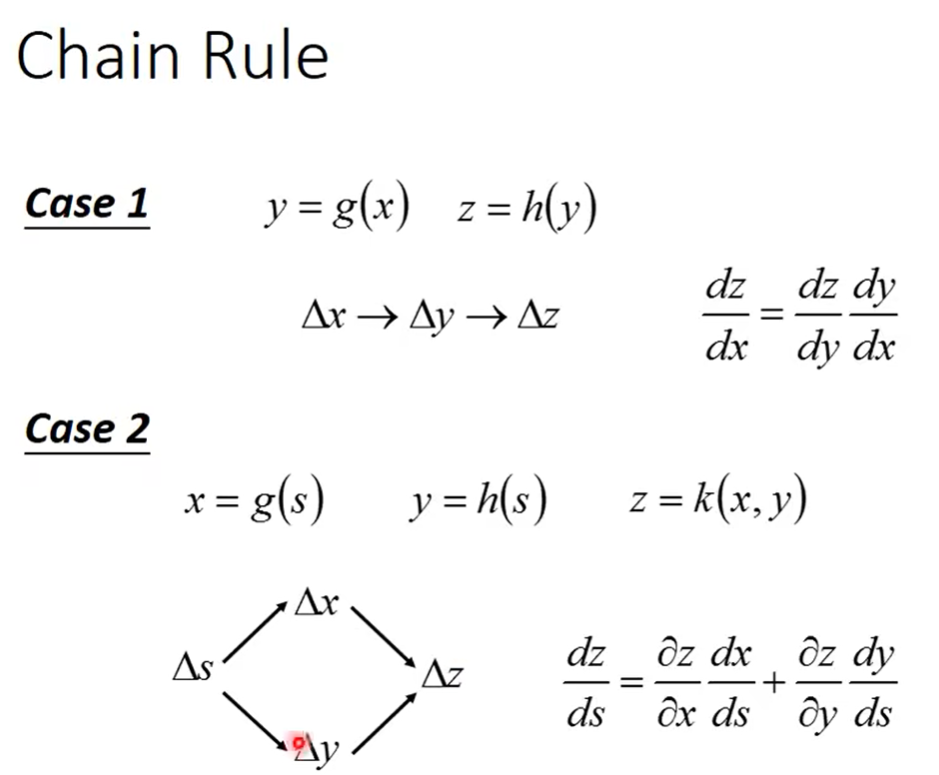
再回到neural network上面。
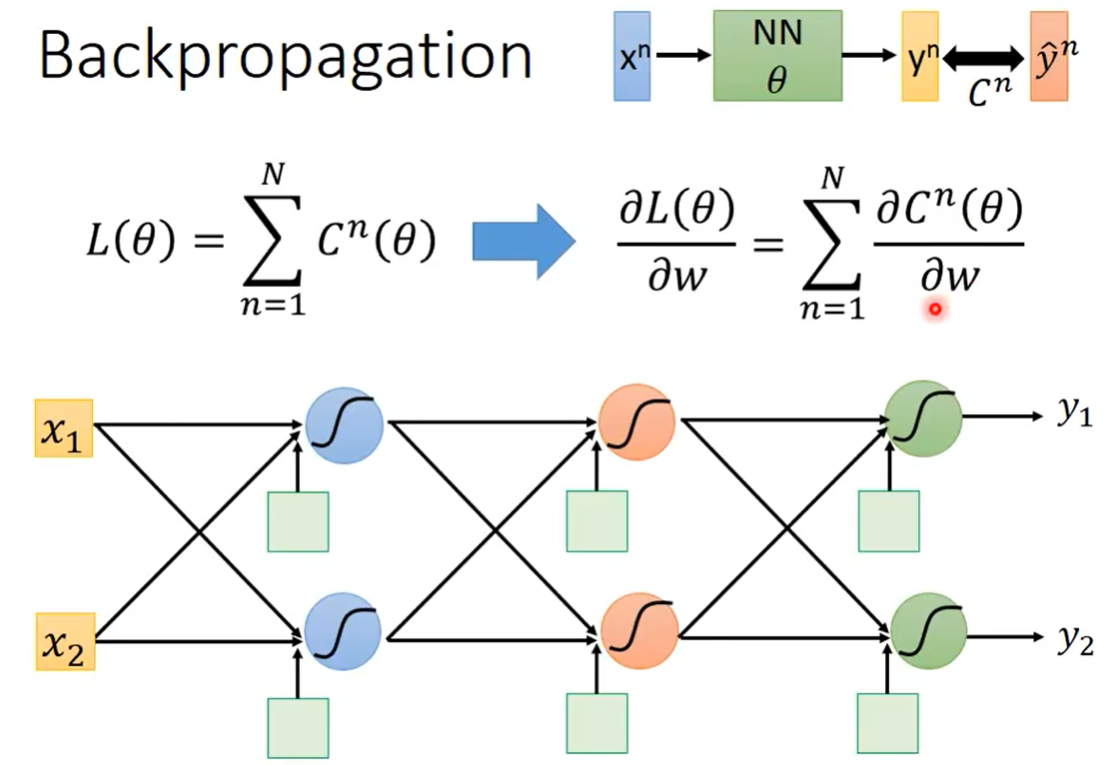
对于一个输入 x n x^n xn,通过计算得到的结果 y n y^n yn,它和真实值 y ^ n \hat y^n y^n之间的差距,就是我们的一个Loss, C n C^n Cn。
把所有的Loss加起来求和,就得到最终的 L ( θ ) L(\theta) L(θ)。
如上图所示,如果此时要对某一个参数比如 w w w求偏微分的话,就得到右边这个式子,即:对整体求偏微分,等于对每个加项求偏微分再求和。
这样考虑有什么好处,好处在于,接下来我们就不用去想着怎么对 L ( θ ) L(\theta) L(θ)整体求偏微分了,而只是去考虑,我们如何去计算,对于某一笔data,我们求它的 C n ( θ ) C^n(\theta) Cn(θ)的偏微分就可以了。这样把每一笔data的求出来,再加和就可以了。
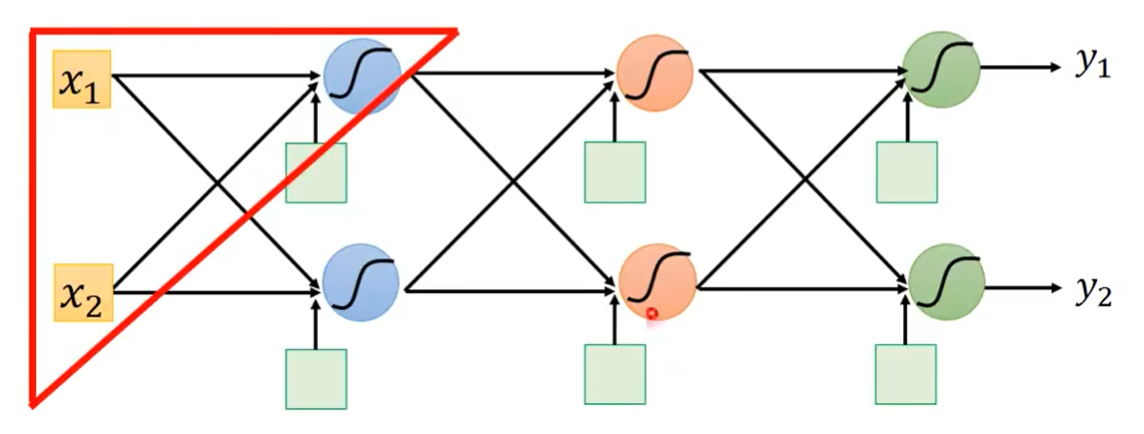
因此,我们从下面这个neural network里面,先只拿一个neural出来去考虑它。
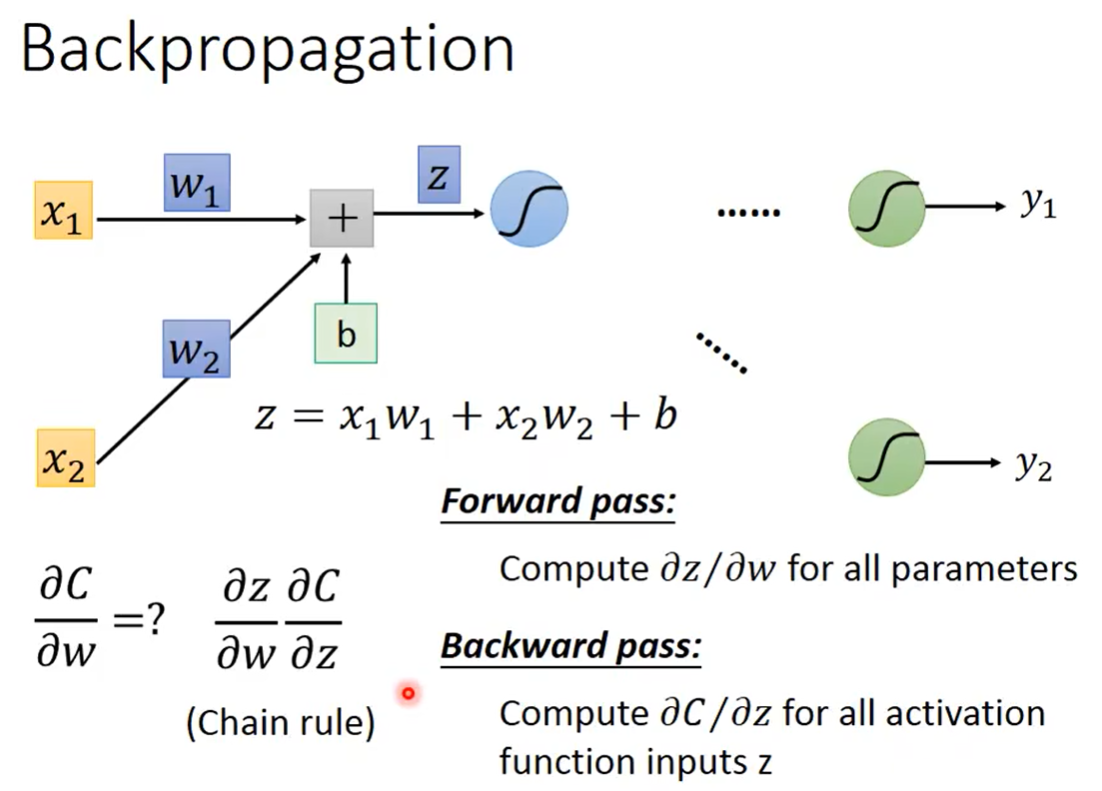
对于一个neuron,假设它如上图所示有两个输入,那么它的计算结果应该是: z = x 1 w 1 + x 2 w 2 + b z=x_1w_1+x_2w_2+b z=x1w1+x2w2+b,根据刚才所说,现在我们要计算它的 ∂ C ∂ w \frac{\partial C}{\partial w} ∂w∂C,结合Chain rule的原理,它等于 ∂ z ∂ w ∂ C ∂ z \frac{\partial z}{\partial w}\frac{\partial C}{\partial z} ∂w∂z∂z∂C。
对于这两项,其中, ∂ z ∂ w \frac{\partial z}{\partial w} ∂w∂z叫做“Forward pass”。对于另一项, ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C被叫做Backward pass。
(2)Forward pass和Backward pass
Forward pass
先来看一下怎么计算 ∂ z ∂ w \frac{\partial z}{\partial w} ∂w∂z。
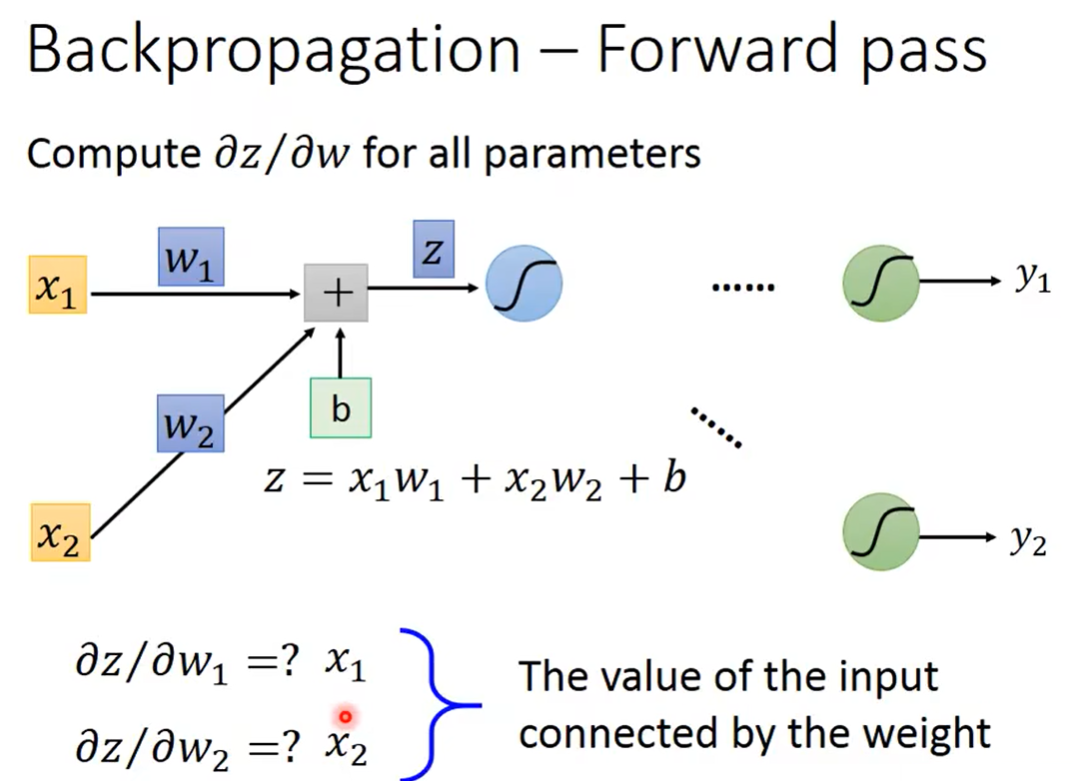
不难计算。但是我们从中可以发现一个规律,就是:这个 w 1 w_1 w1前面接的是 x 1 x_1 x1,所以它的微分就是 x 1 x_1 x1;这个 w 2 w_2 w2前面接的是 x 2 x_2 x2,所以它的微分就是 x 2 x_2 x2。
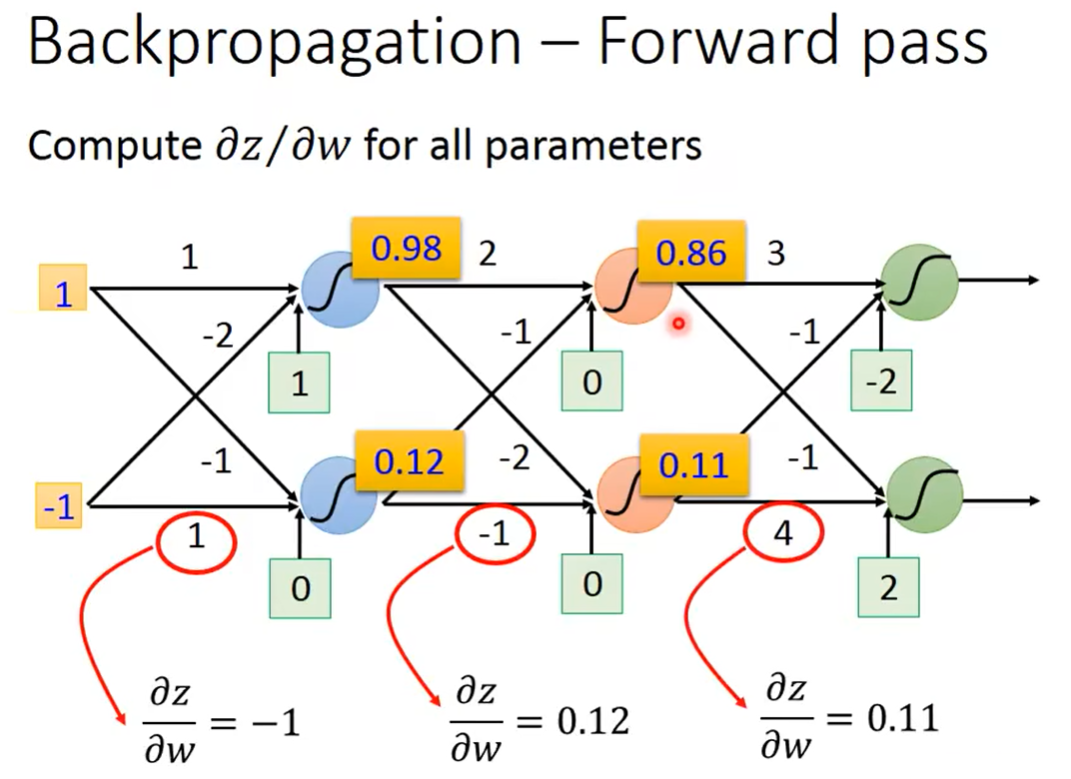
所以,假如给你一个neural network,此时计算任何一个 ∂ z ∂ w \frac{\partial z}{\partial w} ∂w∂z都会变得非常容易,因为我们发现的一个规律是,只需要看这个 w w w对应的input是什么即可。
Backward pass
对于 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C来说,似乎它的计算就比较复杂了。
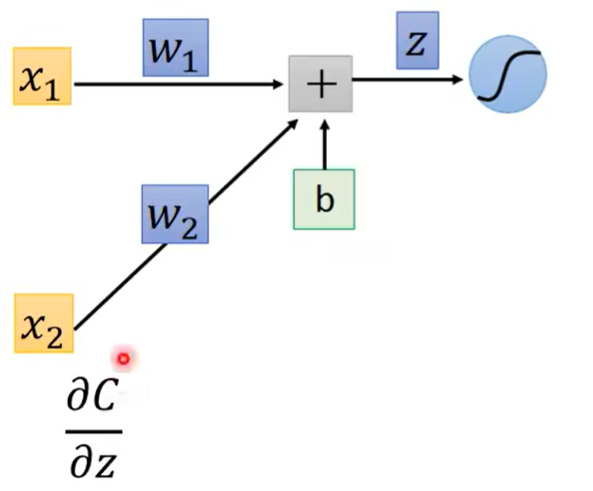
因为,在得到z之后,在这之后还要经过一个复杂的计算过程,才会得到C。(因为C是根据最终的计算结果y,与真实值 y ^ \hat y y^对比得出的)
不过在此,我们可以用Chain Rule对此再做一个拆解。
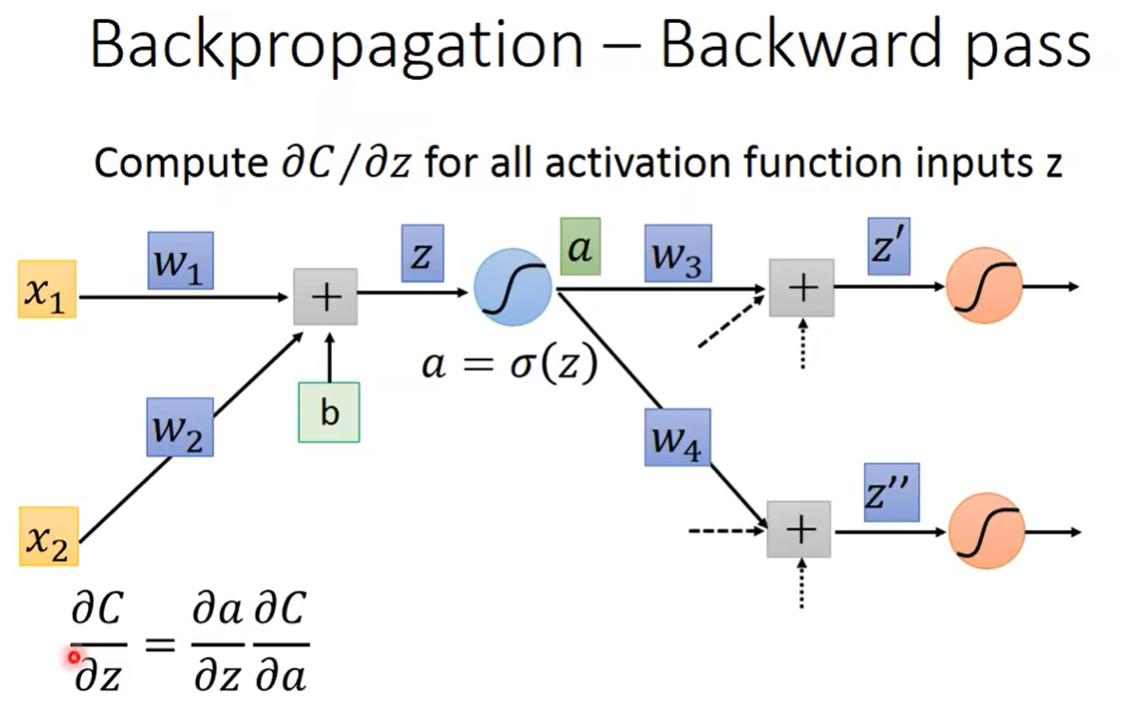
此处我们向后多考虑一层。这一层计算出的z经过一个激活函数,例如Sigmoid函数,即 a = σ ( z ) a=\sigma(z) a=σ(z),它在下一层当中作为其中一个input。如上图所示,它在下一层中作为一个input的时候,它会再乘上它对应的 w w w,与另一个input乘对应w相加,去计算下一层的 z ′ z' z′和 z ′ ′ z'' z′′。(注:此处举的例子里面每层是有两个neuron,实际上会有更多个)
使用Chain Rule,我们可以写出 ∂ C ∂ z = ∂ a ∂ z ∂ C ∂ a \frac{\partial C}{\partial z}=\frac{\partial a}{\partial z}\frac{\partial C}{\partial a} ∂z∂C=∂z∂a∂a∂C。
对于 ∂ a ∂ z \frac{\partial a}{\partial z} ∂z∂a,很好计算,因为我们知道 a = σ ( z ) a=\sigma(z) a=σ(z),我们只需要求 σ ′ ( z ) \sigma'(z) σ′(z)即可。也可以看一下下图,绿色的是Sigmoid函数,紫色的是它的导函数。
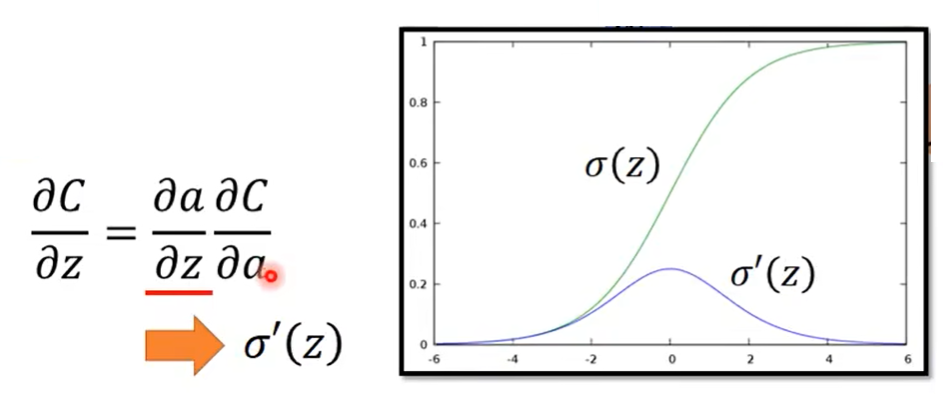
接下来的问题就是 ∂ C ∂ a \frac{\partial C}{\partial a} ∂a∂C应该长什么样子呢?
先不考虑那么遥远,先考虑a对下一层的影响。如图,我们知道,a会影响 z ′ z' z′, z ′ z' z′会影响最终的C;a会影响 z ′ ′ z'' z′′, z ′ ′ z'' z′′会影响最终的C。总之,先不考虑那么多,对于后面这一层而言,a总之要先透过 z ′ z' z′和 z ′ ′ z'' z′′去影响C。
所以,就像Chain Rule的Case 2那样,此处我们可以写成: ∂ C ∂ a = ∂ z ′ ∂ a ∂ C ∂ z ′ + ∂ z ′ ′ ∂ a ∂ C ∂ z ′ ′ \frac{\partial C}{\partial a}=\frac{\partial z'}{\partial a}\frac{\partial C}{\partial z'}+\frac{\partial z''}{\partial a}\frac{\partial C}{\partial z''} ∂a∂C=∂a∂z′∂z′∂C+∂a∂z′′∂z′′∂C。(因为我们举的例子当中是每层只有两个neuron,所以此处是有两个部分,如果有更多个neuron,那么式子会有更多项之和)
对于这个式子,我们仍然是要去计算它。对于其中的 ∂ z ′ ∂ a \frac{\partial z'}{\partial a} ∂a∂z′,怎么算?很简单,就是 w 3 w_3 w3,因为 z ′ = a w 3 + . . . z'=aw_3+... z′=aw3+...;同理, ∂ z ′ ′ ∂ a \frac{\partial z''}{\partial a} ∂a∂z′′就是 w 4 w_4 w4。

接下来的问题就是: ∂ C ∂ z ′ \frac{\partial C}{\partial z'} ∂z′∂C和 ∂ C ∂ z ′ ′ \frac{\partial C}{\partial z''} ∂z′′∂C怎么算?——此处我们同样面临着刚才的问题:在 z ′ z' z′和 z ′ ′ z'' z′′这一层之后,同样还会发生很多很多的事情,还要做很复杂的计算,最终才能得到y,才能得到C。所以我们一下子不知道C对z’或者C对z’'该怎么算。

此处我们先假设这两项我们已经通过某种方法算出来了。先不管为什么,总之我们假设这两项已经被我们算出来了。
那么,至此,整个 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C就能够计算出了。
∂ C ∂ z = σ ′ ( z ) [ w 3 ∂ C ∂ z ′ + w 4 ∂ C ∂ z ′ ′ ] \frac{\partial C}{\partial z}=\sigma'(z)[w_3\frac{\partial C}{\partial z'}+w_4\frac{\partial C}{\partial z''}] ∂z∂C=σ′(z)[w3∂z′∂C+w4∂z′′∂C]
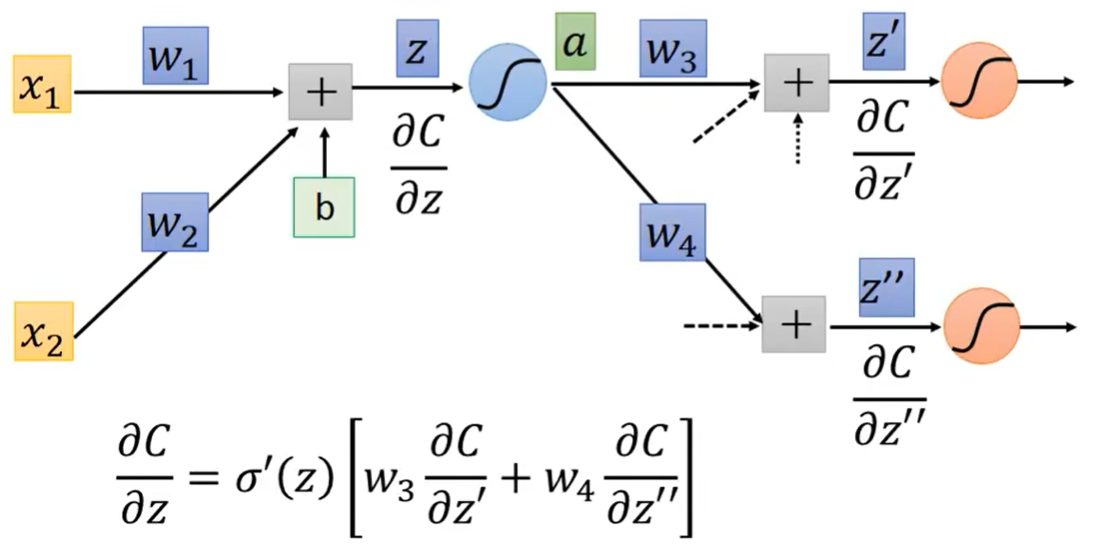
其实到这里,我们可以这样说:只要我们知道了 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C和 ∂ C ∂ z ′ ′ \frac{\partial C}{\partial z''} ∂z′′∂C是多少,我们就可以计算出 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C了。
对此,我们直接从另外一个视角来观察这个式子,如下图所示:
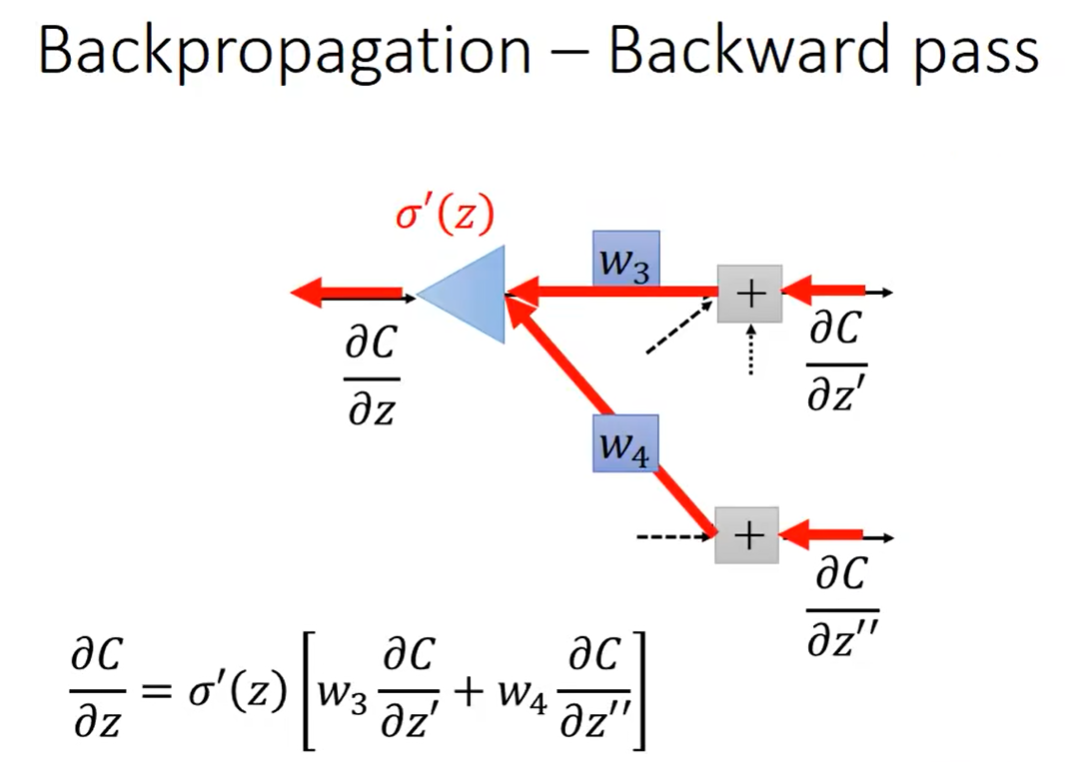
此处我们可以把它理解成一个“特殊的neuron”,这个neuron的input,就是 ∂ C ∂ z ′ \frac{\partial C}{\partial z'} ∂z′∂C和 ∂ C ∂ z ′ ′ \frac{\partial C}{\partial z''} ∂z′′∂C,它们分别乘上各自的权重 w 3 w_3 w3和 w 4 w_4 w4,加和之后再乘上一个 σ ′ ( z ) \sigma'(z) σ′(z)就得到output,就是 ∂ C ∂ z \frac{\partial C}{\partial z} ∂z∂C。
注意, σ ′ ( z ) \sigma'(z) σ′(z)是一个常数,因为它在我们计算Forward pass的过程中就已经被计算好了,而不是一个函数。
现在的情况是:“假设 ∂ C ∂ z ′ \frac{\partial C}{\partial z'} ∂z′∂C和 ∂ C ∂ z ′ ′ \frac{\partial C}{\partial z''} ∂z′′∂C已经被计算出来的情况下,所有问题就都被解决了。——那 ∂ C ∂ z ′ \frac{\partial C}{\partial z'} ∂z′∂C和 ∂ C ∂ z ′ ′ \frac{\partial C}{\partial z''} ∂z′′∂C怎么算呢?
Case 1.Output Layer
第一种情况,假设后面这一层的output已经是整个neural network的输出层了。
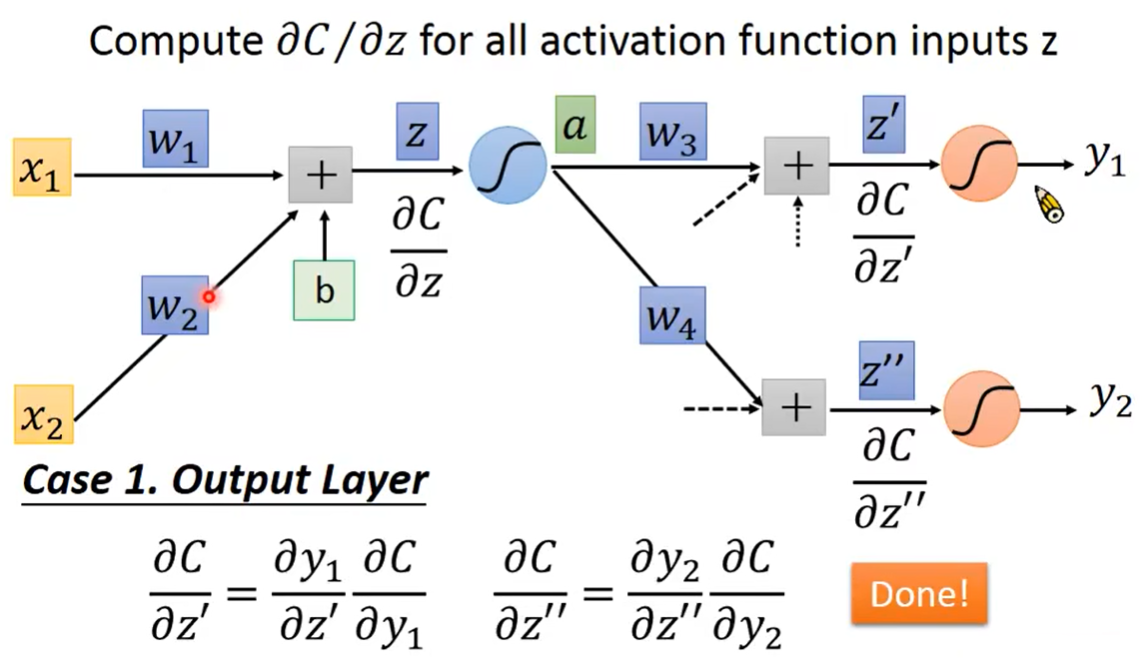
这时就很好算,因为 y 1 y_1 y1是 z ′ z' z′的函数,而损失函数C也是 y y y的函数,所以它们的偏导都很容易能算出。
Case 2.Not Output Layer

如果红色的这一层不是最后一层,而是在它后面还有很多复杂的过程,怎么办?
同样的道理,它也是来自于它后面一层,如上图所示。——反复的继续下去,总有一次我们会得到上面Case 1的情况,就有解了。
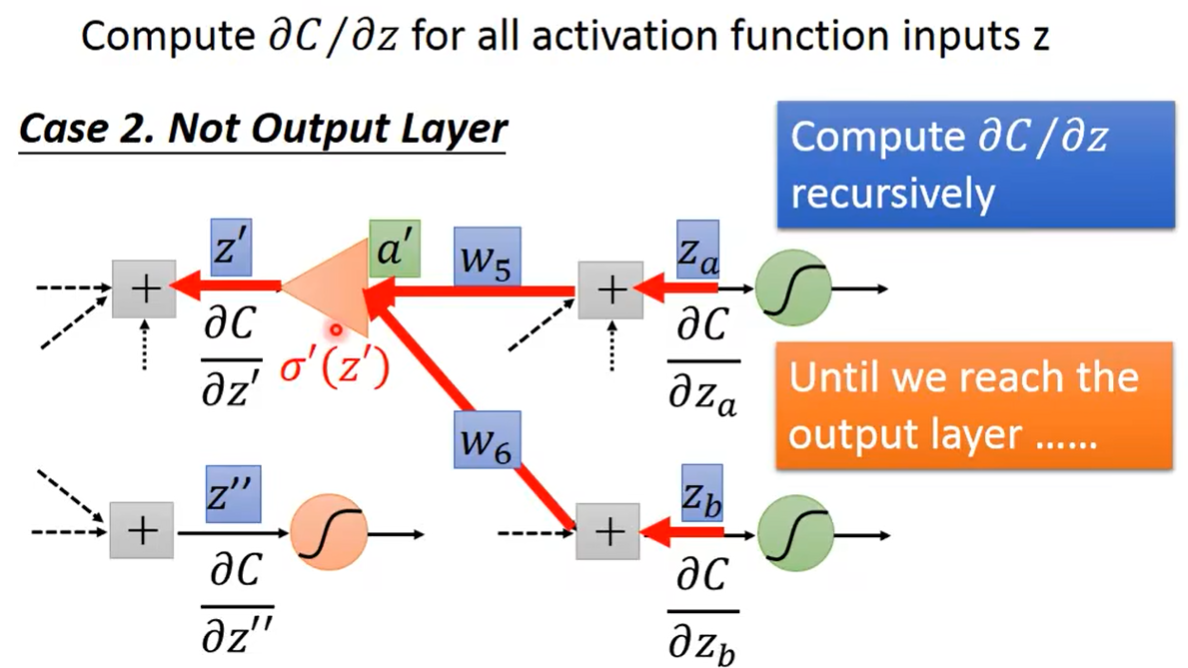
至此,你可能会觉得有点崩溃。假如这个网络有10层Layer,那么对于这个偏微分的计算公式,就会是一个很可怕的式子。从前往后不停地展开、嵌套……。
但是实际上并不是你想的那样,你只需要换一个视角,从后往前看,即从Output Layer开始算。——你会发现,它的运算量,和刚才我们讲的Forward pass是一样的。
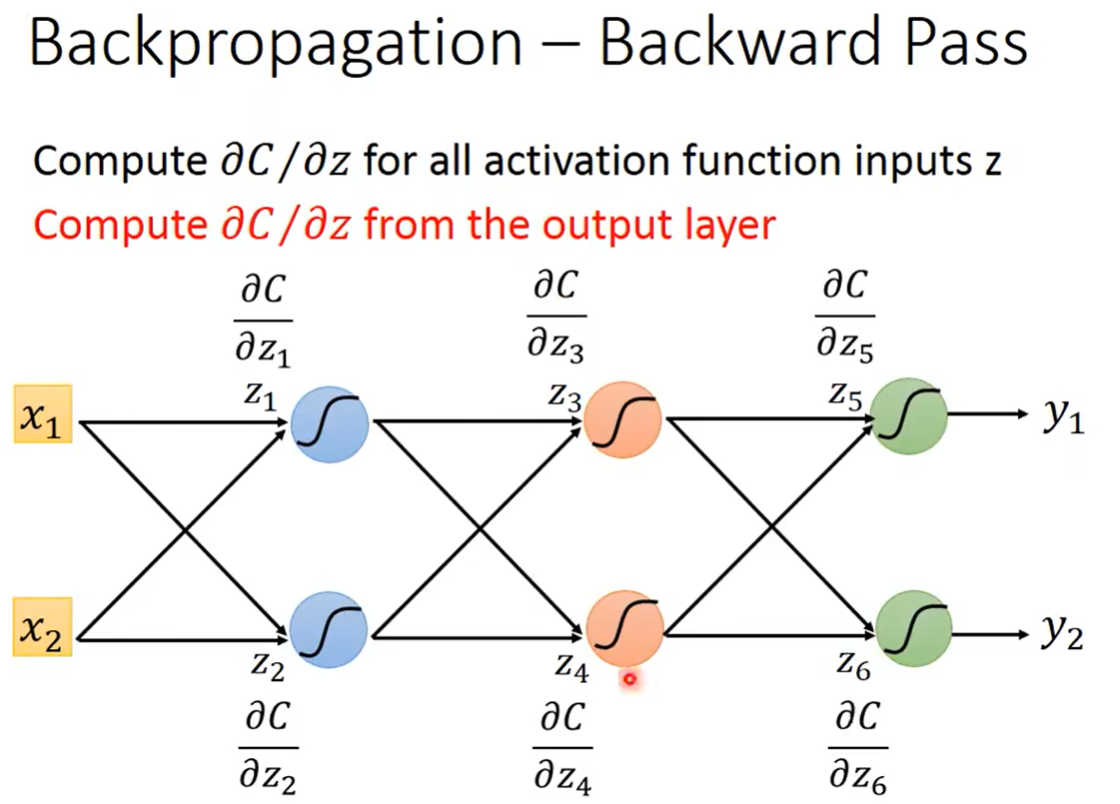
把它从后往前视为一个特殊的neural network就可以了。
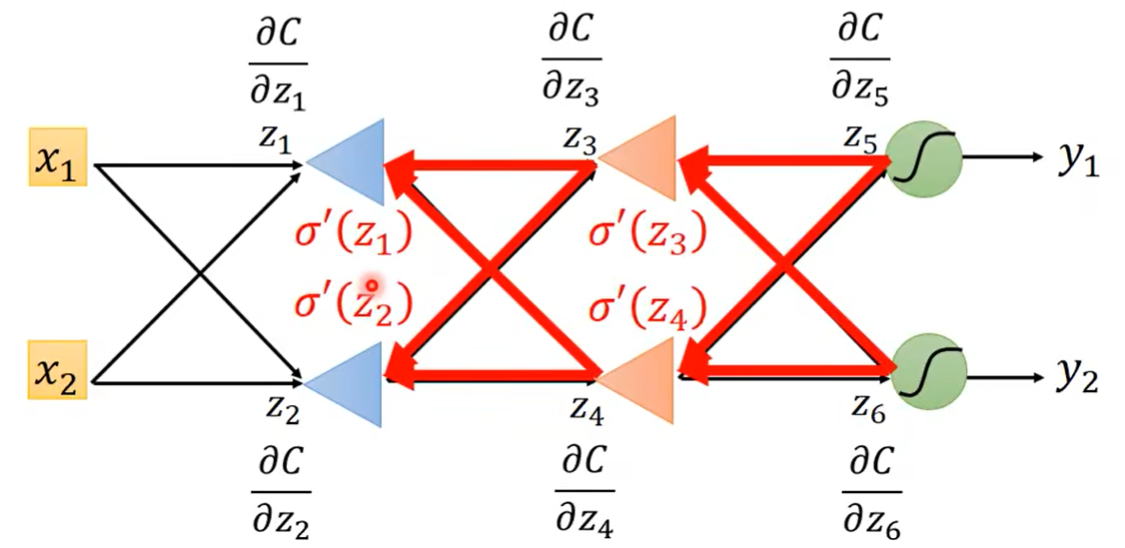
重新思考一下,实际上Backpropagation就是重新建了一个neural network,它的最初input就是最后一层的偏微分,并且它每层的 σ ′ ( z ) \sigma'(z) σ′(z)要首先经过一轮Forward pass才能获取。除此之外,就和一个普通的neural network运算是一样的。