附加动量的 BP 网络学习改进算法详解

一、引言

BP（Back Propagation）神经网络是一种经典的神经网络模型，广泛应用于模式识别、函数逼近、数据分类等众多领域。然而，传统的 BP 算法存在一些局限性，如收敛速度慢、容易陷入局部极小值等问题。为了克服这些问题，研究者们提出了各种改进算法，其中附加动量的 BP 网络学习算法是一种有效的改进方法。本文将详细阐述附加动量的 BP 网络学习改进算法的原理、实现步骤以及通过代码示例展示其具体实现过程。

二、传统 BP 网络学习算法回顾

（一）网络结构与前向传播

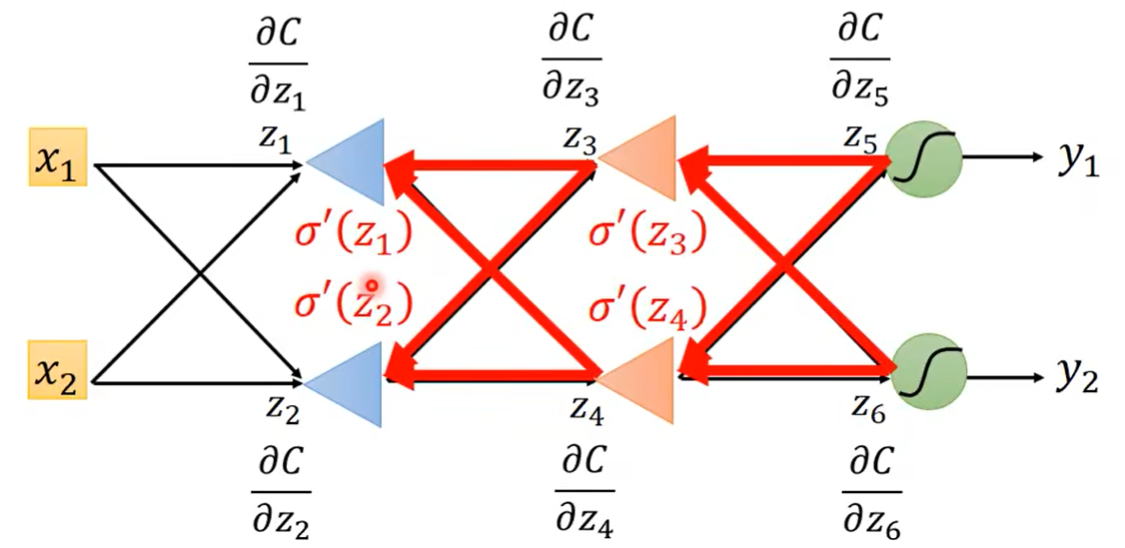
BP 神经网络一般包括输入层、一个或多个隐藏层和输出层。设输入层有 $n$ 个神经元，输入向量为 $\mathbf{x}=(x_1,x_2,\cdots,x_n)$ ；隐藏层有 $h$ 个神经元，输出向量为 $\mathbf{h}=(h_1,h_2,\cdots,h_h)$ ；输出层有 $m$ 个神经元，输出向量为 $\mathbf{y}=(y_1,y_2,\cdots,y_m)$ 。

在前向传播过程中，对于输入层到隐藏层，隐藏层神经元的输入为：

$net_{j}=\sum_{i = 1}^{n}w_{ij}x_{i}+b_{j}$

其中， $w_{ij}$ 是输入层神经元 $i$ 到隐藏层神经元 $j$ 的连接权重， $b_{j}$ 是隐藏层神经元 $j$ 的偏置。隐藏层神经元的输出通常经过激活函数 $f(\cdot)$ 处理，如常用的 Sigmoid 函数 $f(x)=\frac{1}{1 + e^{-x}}$ ，则 $h_{j}=f(net_{j})$ 。

类似地，对于隐藏层到输出层，输出层神经元的输入为：

$net_{k}=\sum_{j = 1}^{h}w_{jk}h_{j}+b_{k}$

输出层神经元的输出为 $y_{k}=f(net_{k})$ 。

（二）误差计算与反向传播

误差计算一般采用均方误差（MSE）准则。对于训练样本集 $\{(\mathbf{x}^{(p)},\mathbf{t}^{(p)})\}_{p = 1}^{P}$ ，其中 $\mathbf{x}^{(p)}$ 是第 $p$ 个输入样本， $\mathbf{t}^{(p)}$ 是对应的目标输出，均方误差为：

$E=\frac{1}{2P}\sum_{p = 1}^{P}\sum_{k = 1}^{m}(y_{k}^{(p)}-t_{k}^{(p)})^{2}$

在反向传播过程中，根据误差函数对权重的梯度来更新权重。以输出层到隐藏层的权重更新为例，根据链式法则，权重 $w_{jk}$ 的更新公式为：

$\Delta w_{jk}=-\eta\frac{\partial E}{\partial w_{jk}}$

其中， $\eta$ 是学习率。对于隐藏层到输入层的权重更新也有类似的公式。具体计算过程中，需要先计算误差对各层输出的偏导数，再通过链式法则逐步计算出对权重的偏导数。

三、传统 BP 算法的问题分析

（一）收敛速度问题

传统 BP 算法在训练过程中，尤其是在处理复杂的非线性问题时，收敛速度往往较慢。这是因为每次权重更新仅基于当前样本的梯度信息，而没有充分利用之前训练过程中的信息。在误差曲面较为平坦的区域，梯度值较小，导致权重更新缓慢，从而延长了训练时间。

（二）局部极小值问题

BP 算法基于梯度下降法，容易陷入局部极小值。在误差曲面中，局部极小值点周围的梯度为零或接近零，使得算法无法继续朝着全局最小值的方向更新权重，导致训练得到的网络性能不佳。

四、附加动量的 BP 网络学习改进算法原理

（一）动量项的引入

附加动量的 BP 算法在传统 BP 算法的基础上，在权重更新公式中添加了动量项。动量项的基本思想是将上一次权重更新的方向和大小考虑进来，使得本次权重更新不仅依赖于当前的梯度信息，还受到之前权重更新趋势的影响。

设当前时刻 $t$ ，对于权重 $w$ ，其更新公式变为：

$\Delta w(t)=\eta\frac{\partial E}{\partial w}+ \alpha\Delta w(t - 1)$

其中， $\eta$ 是学习率， $\alpha$ 是动量系数（通常取值在 0 和 1 之间）， $\Delta w(t - 1)$ 是上一次权重 $w$ 的更新量。

（二）动量项的作用机制

加速收敛
在误差曲面较为平坦的区域，梯度值较小，但由于动量项的存在，它可以继承之前的更新趋势，使得权重更新不会停滞，从而加快了收敛速度。例如，当连续几个训练步骤中梯度方向基本一致时，动量项会累积这种趋势，使权重更新朝着这个方向加速进行。
跳出局部极小值
当算法陷入局部极小值附近时，当前的梯度信息可能会使权重更新停止。而动量项可以使权重更新具有一定的惯性，有可能跳过局部极小值区域，继续向全局最小值方向搜索。因为动量项可以使权重更新方向不完全依赖于当前局部的梯度信息，而是综合了之前的更新历史。

五、附加动量的 BP 网络学习改进算法实现步骤

（一）初始化

权重和偏置初始化
随机初始化网络的连接权重 $w_{ij}$ 和 $w_{jk}$ 以及偏置 $b_{j}$ 和 $b_{k}$ 。通常权重可以在一个较小的范围内随机取值，如 $[- 0.5, 0.5]$ 。
动量项初始化
对于每个权重和偏置，初始化其动量项为零。例如，对于权重 $w_{ij}$ ，其动量项 $\Delta w_{ij}(0)=0$ 。

（二）训练过程

前向传播
对于每个训练样本，按照传统 BP 算法的前向传播方式计算网络的输出，即依次计算输入层到隐藏层、隐藏层到输出层的神经元输出。
误差计算与反向传播
计算当前样本的误差，并根据误差进行反向传播计算梯度。对于输出层到隐藏层和隐藏层到输入层的权重，分别计算其梯度。
权重更新
根据附加动量的权重更新公式更新权重。以权重 $w_{jk}$ 为例，计算当前梯度 $\frac{\partial E}{\partial w_{jk}}$ ，然后更新权重：

$\Delta w_{jk}(t)=\eta\frac{\partial E}{\partial w_{jk}}+ \alpha\Delta w_{jk}(t - 1)$

$w_{jk}(t)=w_{jk}(t - 1)-\Delta w_{jk}(t)$

对于偏置的更新也有类似的步骤。

重复训练
对所有训练样本重复上述步骤，完成一次训练迭代（epoch）。多次重复训练迭代，直到满足训练停止条件，如达到预定的训练次数、误差小于某个阈值等。

六、代码示例

以下是使用 Python 实现附加动量的 BP 网络学习改进算法的代码示例：

import numpy as np# Sigmoid 激活函数
def sigmoid(x):return 1 / (1 + np.exp(-x))# Sigmoid 函数的导数
def sigmoid_derivative(x):return x * (1 - x)class NeuralNetwork:def __init__(self, input_size, hidden_size, output_size):self.input_size = input_sizeself.hidden_size = hidden_sizeself.output_size = output_size# 随机初始化权重self.W1 = np.random.rand(self.input_size, self.hidden_size)self.b1 = np.zeros((1, self.hidden_size))self.W2 = np.random.rand(self.hidden_size, self.output_size)self.b2 = np.zeros((1, self.output_size))# 初始化动量项self.delta_W1 = np.zeros_like(self.W1)self.delta_b1 = np.zeros_like(self.b1)self.delta_W2 = np.zeros_like(self.W2)self.delta_b2 = np.zeros_like(self.b2)self.momentum = 0.9  # 动量系数self.learning_rate = 0.1  # 学习率def forward_propagation(self, X):self.z1 = np.dot(X, self.W1) + self.b1self.a1 = sigmoid(self.z1)self.z2 = np.dot(self.a1, self.W2) + self.b2self.a2 = sigmoid(self.z2)return self.a2def back_propagation(self, X, y):m = X.shape[0]dZ2 = self.a2 - ydW2 = np.dot(self.a1.T, dZ2) / mdb2 = np.sum(dZ2, axis=0, keepdims=True) / mdZ1 = np.dot(dZ2, self.W2.T) * sigmoid_derivative(self.a1)dW1 = np.dot(X.T, dZ1) / mdb1 = np.sum(dZ1, axis=0, keepdims=True) / mreturn dW1, db1, dW2, db2def update_weights(self, dW1, db1, dW2, db2):# 更新隐藏层到输出层的权重和偏置self.delta_W2 = self.learning_rate * dW2 + self.momentum * self.delta_W2self.W2 -= self.delta_W2self.delta_b2 = self.learning_rate * db2 + self.momentum * self.delta_b2self.b2 -= self.delta_b2# 更新输入层到隐藏层的权重和偏置self.delta_W1 = self.learning_rate * dW1 + self.momentum * self.delta_W1self.W1 -= self.delta_W1self.delta_b1 = self.learning_rate * db1 + self.momentum * self.delta_b1self.b1 -= self.delta_b1def train(self, X, y, epochs):for epoch in range(epochs):output = self.forward_propagation(X)dW1, db1, dW2, db2 = self.back_propagation(X, y)self.update_weights(dW1, db1, dW2, db2)if epoch % 100 == 0:error = np.mean((output - y) ** 2)print(f'Epoch {epoch}: Error = {error}')

你可以使用以下方式测试这个神经网络：

# 示例用法
X = np.array([[0, 0], [0, 1], [1, 0], [1, 1]])
y = np.array([[0], [1], [1], [0]])
neural_network = NeuralNetwork(2, 3, 1)
neural_network.train(X, y, 1000)

七、总结

附加动量的 BP 网络学习改进算法通过引入动量项有效地解决了传统 BP 算法收敛速度慢和容易陷入局部极小值的问题。通过在权重更新公式中考虑上一次权重更新的信息，使得算法在训练过程中更加稳定和高效。代码示例展示了该算法在 Python 中的实现过程，通过实际运行可以观察到其在训练神经网络时的性能提升。在实际应用中，需要根据具体的问题和数据集合理选择学习率和动量系数等参数，以进一步优化算法的性能。这种改进算法在众多需要使用 BP 神经网络的领域中具有重要的应用价值，能够提高模型训练的质量和效率。