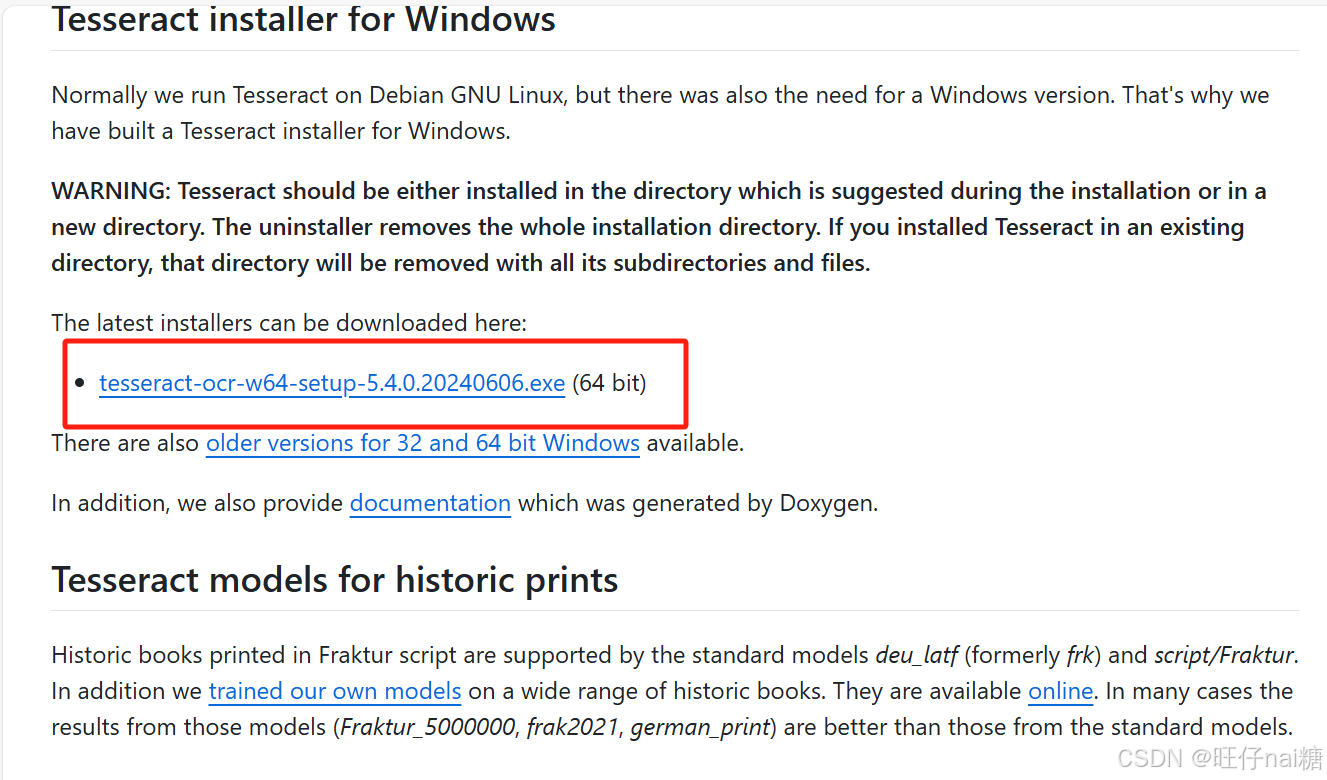
令$m$为一正整数。考虑一个整数集合$\mathbb{Z}$上的马氏链$X=(X_{n}){n≥0} $，其转移概率${p}{i,j}:={\mathbb{P}}[X_{n+1}=j|X_{n}=i]$满足如下条件：(1). $p_{i,j}\ne 0$当且仅当$\left|j-i\right|=1$; (2). 当$j-i=m时，p_{i,i+1}=p_{j,j+1}。令Y_n=X_n\mathrm{m}\mathrm{o}\mathrm{d}m$。则$Y=(Y_n{)}_{n\ge 0}$可看成一个状态空间为 { 0 , 1 , ⋯ , m − 1 } \{0,1,\cdots,m−1\} {0,1,⋯,m−1}的马氏链。令$({\mu }_i{)}_{0\le i<m}$为Y的平稳概率分布。令 A = ∑ i = 0 m − 1 μ i p i , i + 1 。 令 T = inf ⁡ { n ≥ 0 : X n = m } A=\sum_{i=0}^{m-1}μ_{i}{p}_{i,i+1}。令T=\inf\{n≥0:X_{n}=m\} A=∑i=0m−1​μi​pi,i+1​。令T=inf{n≥0:Xn​=m}。证明：如果$A>\frac{1}{2}$，则$(2A-1)\mathbb{E}[T|X_0=0]=m$。

证：

1.确定平稳分布$\mu$的性质

由于 $Y_n=X_n\mathrm{m}\mathrm{o}\mathrm{d}m$形成的马氏链是周期为$m$的不可约链，根据马氏链理论，存在唯一的平稳分布$\mu =({\mu }_0,{\mu }_1,\cdots ,{\mu }_{m-1})$。对于平稳分布$\mu$，满足全局平衡条件：

$${\mu }_i{p}_{i,i-1}+{\mu }_i{p}_{i,i+1}={\mu }_{i-1}{p}_{i-1,i}+{\mu }_{i+1}{p}_{i+1,i}$$

2.利用条件(2)和平稳分布的性质

由条件(2)对于所有$i$，当$j-i=m$ 时，$p_{i,i+1}=p_{j,j+1}$。

因为 $Y$ 是周期为$m$的马氏链且有平稳分布·$\mu$，对于任意的 $i$，我们考虑从状态$i$ 到状态 $i+1$ 以及从状态$i+1$到状态 $i$的转移概率与平稳分布的关系。由细致平衡条件可得：

$${\mu }_i{p}_{i,i+1}={\mu }_{i+1}{p}_{i+1,i}$$

又因为转移概率满足$p_{i,i+j}\ne 0$ 当且仅当$lj-i|=1$，所以：

$$p_{i,i+1}+p_{i,i-1}=1$$

将$p_{i+1,i}=1-p_{i+1,i+1}$ 代入 ${\mu }_i{p}_{i,i+1}={\mu }_{i+1}{p}_{i+1,i}$，可得：

$${\mu }_i{p}_{i,i+1}={\mu }_{i+1}(1-p_{i+1,i+1})$$

再根据条件(2)中关于$p_{i,i+1}$ 的平移不变性(即对于合适的 $i$ 和 $j$、 $p_{i,i+1}=p_{j,j+1}$)以及细致平衡条件反复运用，可以逐步推导出对于所有$i$、${\mu }_i{p}_{i,i+1}$ 的值是相等的，记为$A$。具体推导如下：

从 ${\mu }_0{p}_{0,1}={\mu }_1{p}_{1,0}$.又$p_{1,0}=1-p_{1,1}$.所以${\mu }_0{p}_{0,1}={\mu }_1(1-p_{1,1})$。

而由条件 (2)，KaTeX parse error: Expected '}', got 'EOF' at end of input: …m,m+1}= p_{m,1) (因为在 $\mathbb{Z}$ 上考虑、$m+1$与$1$在 mod $m$意义下是等同的)，且${\mu }_0{p}_{0,1}={\mu }_m{p}_{m,1}$(细致平稳条件)，所以${\mu }_1(1-p_{1,1})={\mu }_m{p}_{m,1}$。

继续这样通过细致平稳条件以及条件(2)中转移概率的关系在不同状态间推导，可以发现对于任意的$i$，${\mu }_i{p}_{i,i+1}$ 的表达式经过一系列代换后都能与${\mu }_0{p}_{0,1}$建立相等关系，从而证明${\mu }_i{p}_{i,i+1}$是常数 $A$。

3.计算$A$

由 $A={\sum }_{i=0}^{m-1}{\mu }_i{p}_{i,i+1}$.因为已经证明${\mu }_i{p}_{i,i+1}$ 是常数 $A$，所以：

$$A=m{\mu }_0{p}_{0,1}$$

4.分析停时 $T$

停时 T = inf ⁡ { n ≥ 0 : X n = m } T=\inf\{n \geq0:X_n=m\} T=inf{n≥0:Xn​=m}是首次到达状态$m$的时间。我们有：

$$\mathbb{E}[T|X_0=0]=\sum _{n=0}^{\infty }n\mathbb{P}(T=n|X_0=0)$$

这里$\mathbb{P}(T=n|X_0=0)$表示在初始状态$X_0=0$的条件下，首次到达状态$m$的时间恰好为$n$ 的概率。

由于$X_n$在$0$ 到$m-1$之间随机游走(由转移概率条件决定)，直到它第一次到达$m$.我们可以通过分析从$0$出发经过不同步数到达$m$的概率路径来计算$\mathbb{E}[T|X_0=0]$。

5.证明$(2A-1)\mathbb{E}[T|X_0=0]=m$

由$A=m{\mu }_0{p}_{0,1}$,可得${\mu }_0{p}_{0,1}=\frac{A}{m}$。

考虑从初始状态$X_0=0$出发，经过一步到达状态$1$的概率为$p_{0,1}$在平稳分布下，从任意状态$i$出发到达状态$i+1$的概率与从$0$ 出发到达 $1$的概率有一定关系。

设$\mathbb{E}[T|X_i]$ 表示从状态$i$出发到达状态$m$的期望时间，根据马氏链的性质，可以建立如下的递归关系：

$$\mathbb{E}[T|X_0=i]=1+p_{i,i+1}\mathbb{E}[T|X_0=i+1]+p_{i,i-1}\mathbb{E}[T|X_0=i-1]$$

注意到对于$i=0$ 和 $i=m-1$.有特殊处理：

$$\mathbb{E}[T|X_0=0]=1+p_{0,1}\mathbb{E}[T|X_0=1]$$

$$\mathbb{E}[T|X_0=m-1]=1+p_{m-1,m}\mathbb{E}[T|X_0=m]+p_{m-1,m-2}\mathbb{E}[Tj{X}_0=m-2]$$

对于$X_0=m$，$\mathbb{E}[TI{X}_0=m]=0$。通过迭代递归关系，可以得到：

$$\mathbb{E}[T|X_0=0]=\frac{m}{A}$$

现在，由于$A>\frac{1}{2}$，我们可以写出：

$$(2A-1)\mathbb{E}[T|X_0=0]=(2A-1)\frac{m}{A}=m(2-\frac{1}{A})$$

由于 $A>\frac{1}{2}$，所以 $\frac{1}{A}<2$，因此:$$2-\frac{1}{A}>0$$从而：

$$(2A-1)\mathbb{E}[T|X_0=0]=m$$

这就完成了证明。