【题解】CF2033G

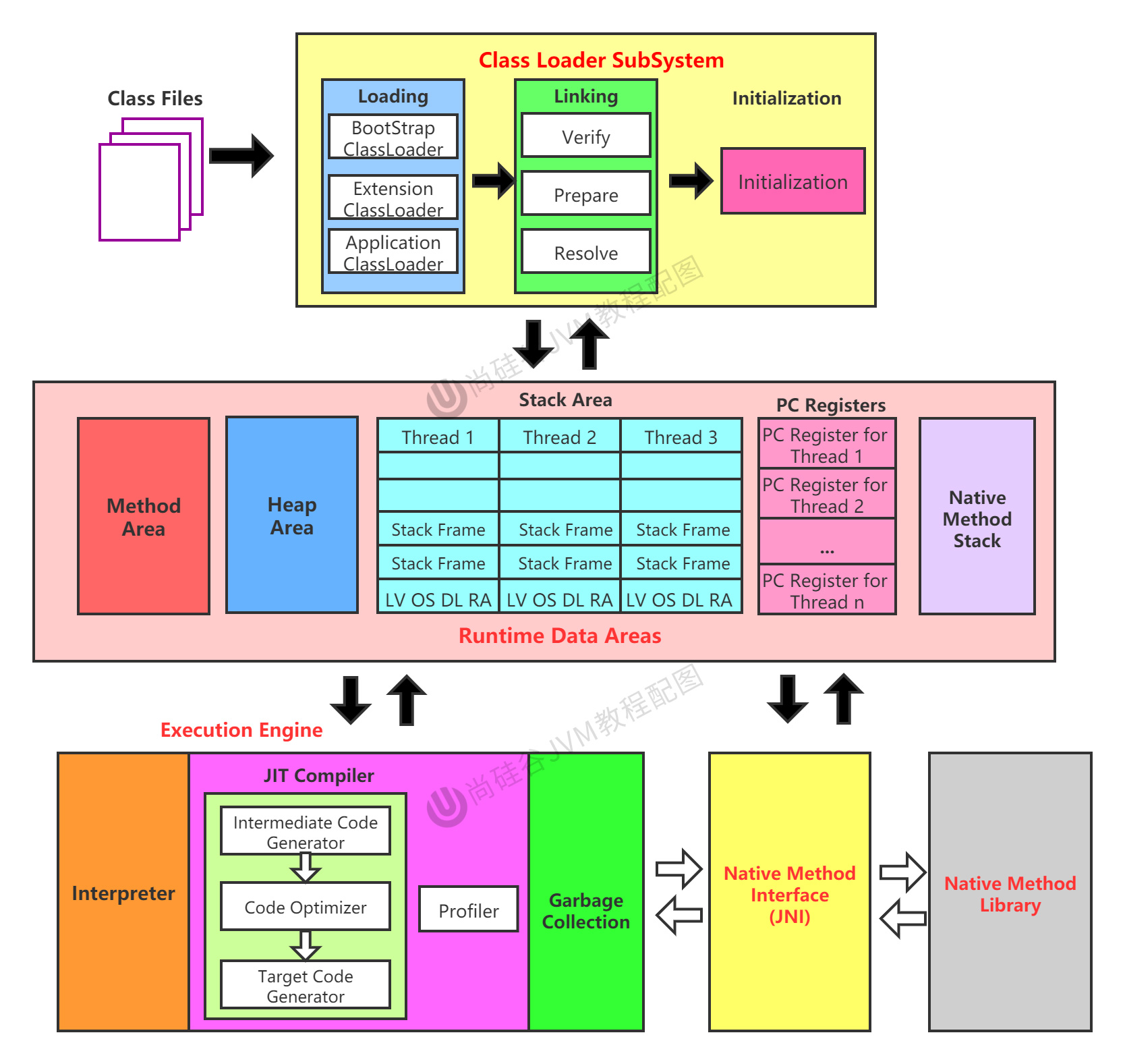
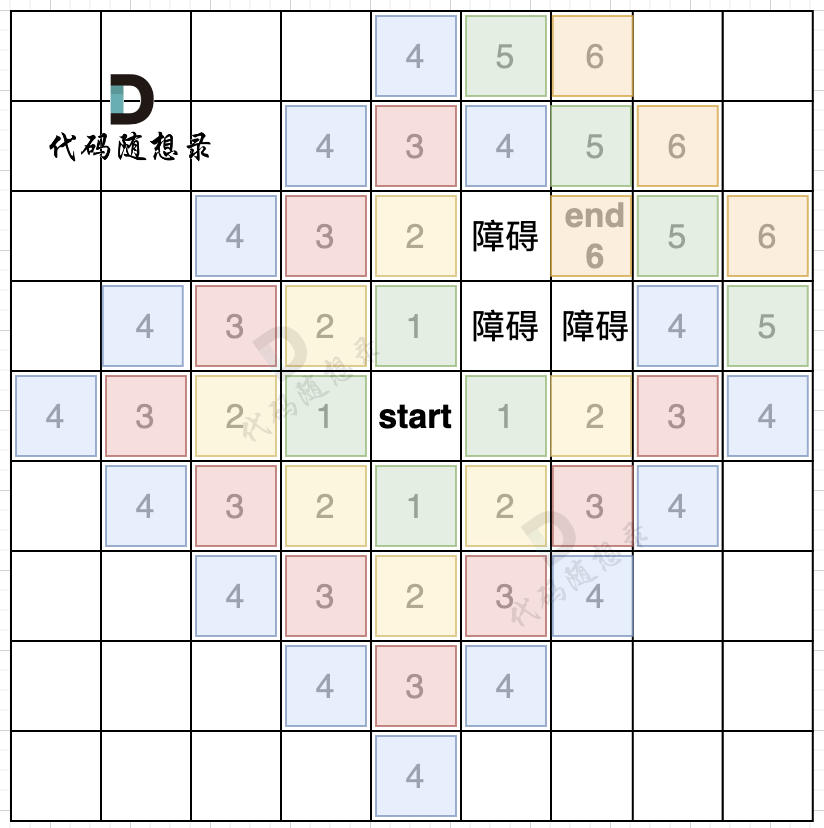
题目

CF2033G
在这里插入图片描述

分析

一道很显然是树形dp的题，但非常恶心QwQ。
先不管复杂度，找找递推关系，一种很直接的想法如下（我觉得是错误的）：

$dp[i][k] = max(dp[fa_{i}][k-1], dp[son_{i,j}[k]+1)$
其中 $d p [i] [k]$ 表示从 $i$ 开始，能量为 $k$ 的最远距离
$fa_{i}$ 表示 $i$ 的根节点， $son_{i,j}$ 表示 $i$ 的第 $j$ 个子节点

这样的问题是会计入这样的路线，实际距离为2，算成了4：
在这里插入图片描述

所以，我们得把向上和向下两种情况分开记录：

$d p 1 [i]$ 表示向下最远距离，由于向下不消耗能量，所以可以少一维
$d p 2 [i] [i d]$ 表示 $i$ 节点如果删掉第 $i d$ 条边后向下最远距离，注意空间限制， $d p 2$ 得用 $v ec t or$ 存储， $i d$ 得另外先预处理好（链式前向星可能会好一点）
$i d [i]$ 表示边 $i, fa_{i})$ 在 $fa_{i}$ 的 $v ec t or$ 中的下标
$h [i]$ 表示节点 $i$ 的深度，根节点深度为 $1$

于是，得到答案的式子为：

$\ from \ \ i] + h[i] - h[j])$

后面的部分看起来很复杂，实际上直接用 $ST$ 表维护即可

代码

#include<bits/stdc++.h>
#define N 200005
#define inf 1000000000
using namespace std;
int t, n, q, fa[N][21], h[N], dp1[N], st[N][21];
int id[N];  // 记录每个根边的id 
vector<int> G[N], dp2[N];   // 去掉边i后向下最远 
void cl() {for(int j=0;(1<<j) <= n;j++) {for(int i=1;i<=n;i++) {st[i][j] = -inf;}}for(int i=1;i<=n;i++) {id[i] = 0;dp1[i] = 0;}for(int i=1;i<=n;i++) {vector<int>().swap(G[i]);vector<int>().swap(dp2[i]);}
}
void init(int x, int pre) {for(int j=1;(1<<j) <= h[x];j++) fa[x][j] = fa[fa[x][j-1]][j-1];for(int i=0;i<G[x].size();i++) {int y = G[x][i];if(y == pre) continue;id[y] = i;h[y] = h[x] + 1;fa[y][0] = x;init(y, x);}
}
void dfs(int x, int pre) {dp1[x] = 0;    // dp1是最大，se是第二大int se = -inf; for(int i=0;i<G[x].size();i++) {int y = G[x][i];if(y == pre) continue;dfs(y, x);if(dp1[y] + 1 >= dp1[x]) {se = dp1[x];dp1[x] = dp1[y] + 1;} else if(dp1[y] + 1 > se) {se = dp1[y] + 1;}}for(int i=0;i<G[x].size();i++) {int y = G[x][i];if(y == pre) {dp2[x].push_back(-inf);continue;}if(dp1[x] == dp1[y] + 1) dp2[x].push_back(se);else dp2[x].push_back(dp1[x]);}
}
void show() {cout<<"showing"<<endl;cout<<"id: "; for(int i=1;i<=n;i++) cout<<id[i]<<' '; cout<<endl;cout<<"h: "; for(int i=1;i<=n;i++) cout<<h[i]<<' '; cout<<endl;cout<<"dp1: ";for(int i=1;i<=n;i++) cout<<dp1[i]<<' ';cout<<endl;for(int i=1;i<=n;i++) {for(int j=0;j<G[i].size();j++) {if(G[i][j] == fa[i][0]) continue;printf("root %d, erase %d, dp2: %d\n", i, G[i][j], dp2[i][j]);}}for(int j=0;(1<<j) <= n; j++) {for(int i=1;i<=n;i++) {if((1<<j) <= h[i]) printf("st[%d][%d]: %d \n" ,i, j, st[i][j]);}}cout<<endl;
}
int main() {cin>>t;while(t--) {cin>>n;cl();for(int i=1;i<=n-1;i++) {int u, v; scanf("%d %d", &u, &v);G[u].push_back(v);G[v].push_back(u);} h[1] = 1; id[1] = -1;init(1, 0);dfs(1, 0);for(int i=2;i<=n;i++)  st[i][0] = dp2[fa[i][0]][id[i]] - h[fa[i][0]]; for(int j=1;(1<<j) <= n;j++) {for(int i=1;i<=n;i++) {if((1<<j) <= h[i]) st[i][j] = max(st[i][j-1], st[fa[i][j-1]][j-1]);}}// show();cin>>q;while(q--) {int v, k; scanf("%d %d", &v, &k);k = min(k, h[v]-1);int ans = dp1[v];int step = log2(k), now = v;for(int step=0;(1<<step) <= k; step++) {if(!(k & (1<<step))) continue;ans = max(ans, st[now][step] + h[v]);now = fa[now][step];}printf("%d ", ans);}}
}