1. 实现链式的二叉树结构

我们之前用顺序表里面数组的底层结构实现了二叉树中堆的结构，但是不是所有的二叉树都具有着堆的性质，所以我们现在需要一个链式结构来描述普遍的二叉树。其底层结构类似一个链表，但是每一个结点由单个区域，一个数据域，用来存储数据，一个是指向左孩子的指针，一个是指向右孩子的指针，这个在前面数据结构之堆（1）的文章里面有提到。所以这个结构的实现结构如下：

//我们可以灵活的使用typedef来进行定义，以便今后方便改变数据类型
typedef char BTDataType;
typedef struct BinaryTreeNode {BTDataType data;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
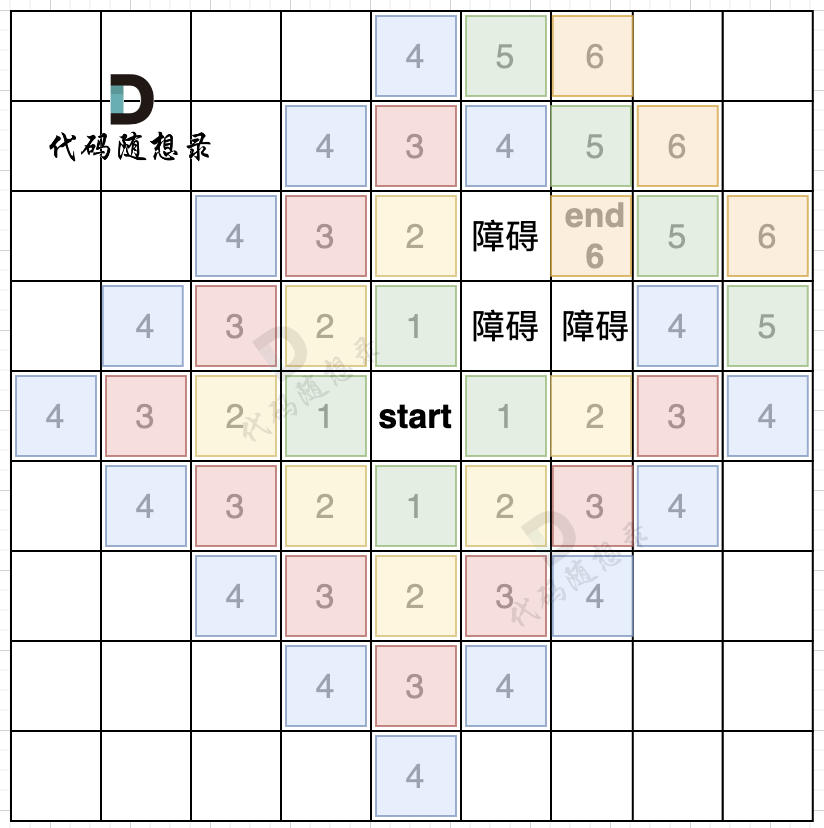
}BTNode;

 通过上面的结构，我们可以试着自己手动创建一个存储着1 2 3 4 5 6 的完全二叉树：

首先链表的手动创建，一定要记住要先写一个创建一个实实在在的结点的函数：

//创建一个二叉树的结点
BTNode* buynode(BTDataType x)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));if (newnode == NULL){perror("malloc fail!");exit(1);}newnode->data = x;newnode->left = newnode->right = NULL;return newnode;
}

 上面和链表思想差不多。

然后就可以手动创建二叉树的链表结构了：

void test()
{BTNode* node1 = buynode(1);BTNode* node2 = buynode(2);BTNode* node3 = buynode(3);BTNode* node4 = buynode(4);BTNode* node5 = buynode(5);BTNode* node6 = buynode(6);node1->left = node2;node1->right = node3;node2->left = node4;node2->right = node5;node3->left = node6;
}

 1.2 前中后序遍历

我们创建一个二叉树的链表结构以后，就不能像堆的数组结构那样通过下标来对二叉树进行遍历。所以在这里我们提供了普遍的前中后序三种遍历方法，我们先大概这三种遍历方法的遍历规则：

前序遍历——“根左右”

中序遍历——“左根右”

后序遍历——“左右根”

 1.2.1 前序遍历

前序遍历的遍历规则是“根左右”，即对于一个结点来说，先把它本身当成临时根结点，以它为根结点，先读取他本身，再读取他的左孩子结点，最后读取他的右孩子结点。

记住，读取到谁就把谁当做临时根节点，直到这个临时根节点的左右结点都为空结点，才可以真正的进行下一步的回归。这就是读取中递归过程中结束条件的重要性！！

比如对于这个二叉树：

它通过前序遍历的结果应该是1 2 3 4 5 6。

 现在我们可以对于前序遍历进行代码的实现，大家可以用自己的已经写好的代码在前面手动创建的二叉树里面进行测试，就可以及时纠正代码的错误。

// 二叉树前序遍历 
void PrevOrder(BTNode* root)
{if (root == NULL)return;printf("%d ", root->data);PrevOrder(root->left);PrevOrder(root->right);
}

 1.2.2 中序遍历

中序遍历的遍历规则是“左根右”，即对于一个结点来说，先把它本身当成临时根结点，以它为根结点，先读取他的左孩子结点，再读取他的本身，最后读取他的右孩子结点。

一样要注意，读取到谁，就先把他当作临时的根结点，一直一直先读取他的左孩子结点，直到左孩子结点为空为止 ，再回归自己，再读取他的右孩子节点。

 用中序遍历法遍历上面的二叉树的话，结果就是3 2 1 5 4 6。

现在对中序遍历进行代码的实现：

// 二叉树中序遍历
void InOrder(BTNode* root)
{if (root == NULL){return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}

 1.2.3 后序遍历

后序遍历的遍历规则是“左右根”，即对于一个结点来说，先把它本身当成临时根结点，以它为根结点，先读取他的左孩子结点，再读取他的右孩子结点，最后读取他本身。

用后序遍历法遍历上面的二叉树的话，结果就是3 2 5 6 4 1。 

现在对后序遍历进行代码的实现：

// 二叉树后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->data);
}

 1.2.4 层序遍历

还有一个方法，是层序遍历，层序遍历的规则就是从上到下依次从左到右读取每一层的数据。

用层序遍历的方法遍历上面的二叉树的话，结果就是1 2 4 3 5 6。 

层序遍历的方法要用到队列的运用，因为队列有一个数据先进先出的规则。

具体的实现方法是：

1.先将二叉树的根结点这个结点（注意不是数据）从队列的队尾进入到队列

2.然后再将它读取出来（放在一个临时变量front里面）

3.再将它从队头删除

4.然后将这个结点的左右孩子结点按左右顺序从队尾依次插入

5.再把此时的第一个结点读取出来。

6.重复这个过程，直到队列为空。

这里需要用到队列，我们在写代码的时候记得引用一下队列的实现代码的头文件和源文件。因为在之前的文章中有详细讲解，这里就不再赘述。

// 层序遍历
//层序遍历的意思是二叉树里每一层的数据从左到右依次遍历
//在这里需要用到队列，因为队列的性质是先入先出
void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);QueuePush(&q, root);//结束条件是一直取一直取，直到把队列里面的数据都取完为止while (!QueueEmpty(&q)){//先取对头这个结点并打印BTNode* front = QueueFront(&q);printf("%d ", front->data);//然后将这个节点删除掉QueuePop(&q);//将这个结点的左右孩子结点放插入进去，空指针就不用放了if (front->left){QueuePush(&q, root->left);}if (front->right){QueuePush(&q, root->right);}}//队列为空QueueDestroy(&q);
}

 判断二叉树是否是完全二叉树

掌握了这个方法后，我们可以利用这个思维进行完全二叉树的判断。我们知道，完全二叉树是一个有序的，除了最后一层以外的层的结点数都是满的，并且最后一层的结点是有序的，所以如果将一个完全二叉树按照上面的方法往队列里面进行插入和提取的话，如果front等于空了，该队列里面的元素也应该全部为空，如果不为空，就证明该二叉树不是完全二叉树。大家可以自己画图举例试验一下。

所以注意，在进行代码实现时候，要记得把空结点也要放进队列当中。

// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{Queue q;QueueInit(&q);QueuePush(&q, root);//结束条件是一直取一直取，直到把队列里面的数据都取完为止while (!QueueEmpty(&q)){//先取对头这个结点BTNode* front = QueueFront(&q);//然后将这个节点删除掉QueuePop(&q);//如果front结点是一个空结点，直接跳出循环,去判断后面的结点里面有没有不为空的节点if (front == NULL){break;}//如果front结点不为空，将这个结点的左右孩子结点放插入进去，空结点也要插入QueuePush(&q, root->left);QueuePush(&q, root->right);}//break后，队列不一定为空while (!QueueEmpty(&q)){//先取对头这个结点BTNode* front = QueueFront(&q);//然后将这个节点删除掉QueuePop(&q);//如果front指针不为空，那就不是完全二叉树if (front != NULL){QueueDestroy(&q);return false;}}//后面都为空指针，那就是完全二叉树QueueDestroy(&q);return true;
}

 1.2.5 链式二叉树结构的其他实现——递归思想

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}// 二叉树叶子节点个数(叶子结点是指没有左右结点的结点)
int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BinaryTreeLevelKSize(root->left, k - 1) + BinaryTreeLevelKSize(root->right, k - 1);
}//求二叉树的深度/高度
int BinaryTreeDepth(BTNode* root)
{if (root == NULL){return 0;}int left = BinaryTreeDepth(root->left);int right = BinaryTreeDepth(root->right);return left > right ? left + 1 : right + 1;
}// 二叉树查找值为x的节点,是各个结点都不一样的情况
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* leftfind = BinaryTreeFind(root->left, x);if (leftfind){return leftfind;}BTNode* rightfind = BinaryTreeFind(root->right, x);if (rightfind){return rightfind;}return NULL;
}// 二叉树销毁
//要进行销毁操作，实参指针也得被销毁，形参的变化如果要影响实参，就得传实参的地址，
// 因为实参是一个一级指针，所以我们得用二级指针来接受实参的地址
void BinaryTreeDestory(BTNode** root)
{//先销毁左子树，再销毁右子树，最后销毁根节点//然后根节点继续是上一个结点左子树，依次递归if (*root == NULL){return;}BinaryTreeDestory(&((*root)->left));BinaryTreeDestory(&((*root)->right));//一直递归到该root的左右节点都为NULL，才可以free掉rootfree(*root);*root == NULL;
}

2. OJ -通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树

 这个需要强烈的递归思想，我总结了一下递归思想的注意事项：

1.一定要注意合适的截止条件

2.在进入递归的时候，要重新将整个程序走一遍，在到达截止条件得到返回值后，一定要注意要继续走完回归的这个函数接下来的函数操作

    //scr就是一个数组指针，n为数组中的元素个数，*pi为数组的下标
BTNode* BinaryTreeCreate(BTDataType* src, int n, int* pi)
{//若*pi大于n（即原数组已经走完）或者走到了#就返回NULLif (*pi >= n || src[*pi] == '#'){(*pi)++;//*pi要一直往后走return NULL;}//要创建好二叉树的结点BTNode* cur = (BTNode*)malloc(sizeof(BTNode));//前序遍历，就按根左右遍历cur->data = src[*pi];(*pi)++;cur->left = BinaryTreeCreate(src, n, pi);cur->right = BinaryTreeCreate(src, n, pi);return cur;
}

希望对大家有所帮助。