条件引导的 diffusion
对于无条件的DDPM 而言
p ( x t ∣ x 0 ) ∼ N ( α t ˉ x 0 , 1 − α t ˉ ⋅ I ) p(x_t | x_0) \sim \mathcal{N}( \sqrt{\bar{\alpha_t}} x_0, 1-\bar{\alpha_t} \cdot \mathrm{I} ) p(xt∣x0)∼N(αtˉx0,1−αtˉ⋅I)
可以得到
log p ( x t ∣ x 0 ) = − 1 2 ( x t − α t ˉ x 0 ) 2 1 − α t ˉ \begin{aligned} \log p(x_t|x_0) &= - \frac{1}{2} \frac{ (x_t - \sqrt{\bar{\alpha_t}} x_0) ^ 2 }{ 1-\bar{\alpha_t} } \end{aligned} logp(xt∣x0)=−211−αtˉ(xt−αtˉx0)2
计算其 score func, 可以得到
∇ x log p ( x t ∣ x 0 ) = − ( x t − α t ˉ x 0 ) 1 − α t ˉ = − ϵ 1 − α t ˉ ≈ − ϵ θ ( x t , t ) 1 − α t ˉ \begin{aligned} \nabla_x \log p(x_t|x_0) &= -\frac{ (x_t - \sqrt{\bar{\alpha_t}} x_0) }{ 1-\bar{\alpha_t} } \\ &= -\frac{ \epsilon } { \sqrt{1-\bar{\alpha_t}} } \\ & \approx -\frac{ \epsilon_{\theta}(x_t, t) }{ \sqrt{1-\bar{\alpha_t}} } \end{aligned} ∇xlogp(xt∣x0)=−1−αtˉ(xt−αtˉx0)=−1−αtˉϵ≈−1−αtˉϵθ(xt,t)
也就是,我们训练的网络conditionalUnet 输出的是噪声的估计, 这个估计的噪声 ϵ θ ( x t , t ) \epsilon_{\theta}(x_t, t) ϵθ(xt,t)可以用来计算当前数据点在整个概率空间中的score-func: ∇ x log p ( x t ∣ x 0 ) \nabla_x \log p(x_t|x_0) ∇xlogp(xt∣x0).
对于 conditional Diffusion. 其 score func 可以写成
∇ x t log p ( x t ∣ y ) = ∇ x t log ( p ( x t ) ⋅ p ( y ∣ x t ) p ( y ) ) = ∇ x t log p ( x t ) + ∇ x t log p ( y ∣ x t ) − ∇ x t log p ( y ) ⏟ = 0 和 x t 无关 = ∇ x t log p ( x t ) ⏟ u n c o n d i t i o n a l s c o r e + ∇ x t log p ( y ∣ x t ) ⏟ a d v e r s i a l g r a d i e n t \begin{aligned} \nabla_{x_t} \log p(x_t|y) &= \nabla_{x_t} \log \left ( \frac{ p(x_t) \cdot p(y|x_t) }{ p(y) } \right) \\ &= \nabla_{x_t} \log p(x_t) + \nabla_{x_t} \log p(y|x_t) - \underbrace{\nabla_{x_t} \log p(y)} _{=0 \ \ 和 x_t 无关} \\ &= \underbrace{ \nabla_{x_t} \log p(x_t)}_{ \mathrm{unconditional\ score} } + \underbrace{ \nabla_{x_t} \log p(y|x_t) }_{ \mathrm{adversial\ gradient} } \end{aligned} ∇xtlogp(xt∣y)=∇xtlog(p(y)p(xt)⋅p(y∣xt))=∇xtlogp(xt)+∇xtlogp(y∣xt)−=0 和xt无关 ∇xtlogp(y)=unconditional score ∇xtlogp(xt)+adversial gradient ∇xtlogp(y∣xt)
现在,我们需要估计 ∇ x t log p ( x t ∣ y ) \nabla_{x_t} \log p(x_t|y) ∇xtlogp(xt∣y) 中的 ϵ ′ \epsilon' ϵ′, 然后使用 DDPM/DDIM 采样即可. 不妨设
∇ x t log p ( x t ∣ y ) = − ϵ ′ 1 − α t ˉ \begin{align} \nabla_{x_t} \log p(x_t|y) &= -\frac{ \epsilon' }{ \sqrt{ 1- \bar{\alpha_t}} } \end{align} ∇xtlogp(xt∣y)=−1−αtˉϵ′
则我们有
∇ x t log p ( x t ∣ y ) = ∇ x t log p ( x t ) + ∇ x t log p ( y ∣ x t ) ⏟ 令 = g − ϵ ′ 1 − α t ˉ = − ϵ 1 − α t ˉ + g 可得 : ϵ ′ = ϵ − 1 − α ˉ t ⋅ g \begin{align} \nabla_{x_t} \log p(x_t|y) &= \nabla_{x_t} \log p(x_t) + \underbrace{ \nabla_{x_t} \log p(y|x_t)}_{ 令 = g } \\ -\frac{ \epsilon' }{ \sqrt{ 1- \bar{\alpha_t}} } &= -\frac{ \epsilon }{ \sqrt{ 1- \bar{\alpha_t}} } + g \\ 可得 &: \epsilon' = \epsilon - \sqrt{1-\bar{\alpha}_t} \cdot g \end{align} ∇xtlogp(xt∣y)−1−αtˉϵ′可得=∇xtlogp(xt)+令=g ∇xtlogp(y∣xt)=−1−αtˉϵ+g:ϵ′=ϵ−1−αˉt⋅g
即我们在无条件模型 DDPM 估计的噪声中添加一个微小的扰动( 1 − α ˉ t ⋅ g \sqrt{1-\bar{\alpha}_t}\cdot g 1−αˉt⋅g),就可以作为条件模型的噪声估计.
-
g = ∇ x t log p ( y ∣ x t ) g = \nabla_{x_t} \log p(y|x_t) g=∇xtlogp(y∣xt) 的含义:
条件概率的梯度: ∇ x t log p ( y ∣ x t ) \nabla_{x_t} \log p(y|x_t) ∇xtlogp(y∣xt) 表示的是在已知 x t x_t xt的情况下,微小变化 x t x_t xt如何影响条件 y y y的对数概率。这是一个 向量场,指向增加条件 y y y出现概率的方向。
-
如何得到
g假设我现在已经有了一个回归模型, 即 y = f ( x t , . . . ) y = f(x_t, ...) y=f(xt,...).
输入一个数据 x t x_t xt, 返回其对应一个 logit 值.
## 输入: x_t, 模型 f x_t = torch.tensor(x_t, requires_grad=True) y = f(x_y) ## pytorch model 预测其结果 log_p = torch.log(y) ## 计算 log 概率 log_p.backward() ## 计算梯度 grad_x_t = x_t.grad ## 获取梯度
Langevin Dynamics 采样
首先,假设我们已经有了一个训练好的score-func( s θ ( x ) s_{\theta}(x) sθ(x)). 已经接近于真实的 s ( x ) s(x) s(x), 即 s θ ( x ) = ∇ x log p θ ( x ) s_{\theta}(x)=\nabla_{x} \log p_{\theta}(x) sθ(x)=∇xlogpθ(x), 其中 p θ ( x ) ≈ p ( x ) p_{\theta}(x) \approx p(x) pθ(x)≈p(x). 现在, 我们需要利用 s θ ( x ) s_{\theta}(x) sθ(x) 对 x 进行采样,使得 x ∼ p θ ( x ) x \sim p_{\theta}(x) x∼pθ(x)
郎之万公式: 描述了粒子做随机布朗运动 (粒子位置随时间变化的关系), 是一种 SDE, 描述了 由梯度力(即. U ( x ( t ) U(x(t) U(x(t))驱动并受到随机噪声(即. Z t Z_t Zt)影响的系统的时间演化.
d X ( t ) = − ∇ x U ( x ( t ) ) ⋅ d t + σ d t ⋅ Z t dX(t) = -\nabla_x U(x(t)) \cdot dt + \sigma \sqrt{dt} \cdot Z_t dX(t)=−∇xU(x(t))⋅dt+σdt⋅Zt
X ( t ) X(t) X(t):
Diffuser 源码解读
DDPMSchedule
1. α , α ˉ , β \alpha, \bar{\alpha}, \beta α,αˉ,β 的关系和计算
x t = α t ⋅ x t − 1 + 1 − α t ⋅ ϵ t = ∏ i = 1 t α i ⋅ x 0 + 1 − ∏ i = 1 t α i ⋅ ϵ 0 = α t ˉ ⋅ x 0 + 1 − α t ˉ ⋅ ϵ 0 β t = 1 − α t \begin{align} x_t &= \sqrt{\alpha_t} \cdot x_{t-1} + \sqrt{ 1-\alpha_t } \cdot \epsilon_t \\ &= \sqrt{\prod_{i=1}^{t} \alpha_i } \cdot x_0 + \sqrt{1-\prod_{i=1}^{t}\alpha_i} \cdot \epsilon_0 \\ &= \sqrt{\bar{\alpha_t}} \cdot x_0 + \sqrt{1-\bar{\alpha_t}} \cdot \epsilon_0 \\ \beta_t &= 1-\alpha_t \end{align} xtβt=αt⋅xt−1+1−αt⋅ϵt=i=1∏tαi⋅x0+1−i=1∏tαi⋅ϵ0=αtˉ⋅x0+1−αtˉ⋅ϵ0=1−αt
-
在
DDPMSchedule中, 先计算出 β t \beta_t βt 的值,然后利用 α t = 1 − β t \alpha_t = 1- \beta_t αt=1−βt 计算剩下的系数。 -
self.beta的计算有各种不同的方法,- trained_betas: 需要传入自定义的beta
- linear
- squaredcos_cap_v2
- …
-
alpha和alpha_cumprod的计算self.alphas = 1.0 - self.betas self.alphas_cumprod = torch.cumprod(self.alphas, dim=0) # 累积乘积(cumulative product) -
self.betas: 是扩散过程中“噪声量”的度量。控制着每一步扩散过程中加入的噪声量的大小. -
self.alphas: 每一步中保留的原始信号的比例。
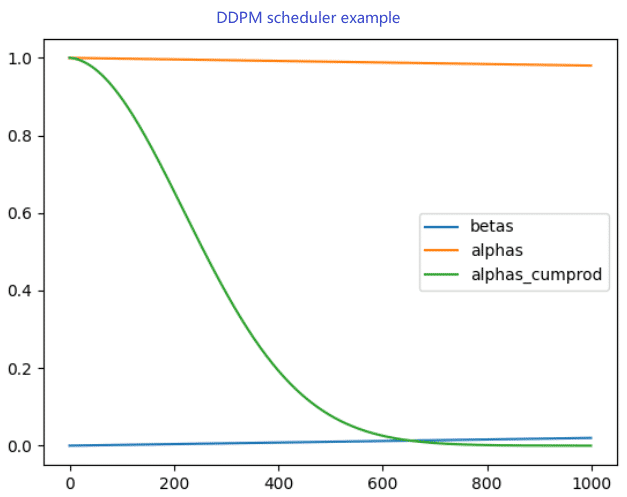
上图是 DDPM 中的 α \alpha α, β \beta β, α ˉ \bar{\alpha} αˉ 的关系。
2. 计算前向时刻的采样: x t → x t − 1 x_t \rightarrow x_{t-1} xt→xt−1
q ( x t − 1 ∣ x t , x 0 ) = q ( x t ∣ x t − 1 , x 0 ) q ( x t − 1 ∣ x 0 ) q ( x t ∣ x 0 ) = N ( x t ; α t x t − 1 , ( 1 − α t ) I ) N ( x t − 1 ; α ˉ t − 1 x 0 , ( 1 − α ˉ t − 1 ) I ) N ( x t ; α ˉ t x 0 , ( 1 − α ˉ t ) I ) ∝ N ( x t − 1 ; α t ( 1 − α ˉ t − 1 ) x t + α ˉ t − 1 ( 1 − α t ) x 0 1 − α ˉ t ⏟ μ q ( x t , x 0 ) , ( 1 − α t ) ( 1 − α ˉ t − 1 ) 1 − α ˉ t I ⏟ Σ q ( t ) ) \begin{align} q(x_{t-1}|x_t, x_0) &= \frac{ q(x_t|x_{t-1}, x_0) q(x_{t-1}|x_0) }{ q(x_t|x_0) }\\ &= \frac{\mathcal{N}(x_{t} ; \sqrt{\alpha_t} x_{t-1}, (1 - \alpha_t)\textbf{I})\mathcal{N}(x_{t-1} ; \sqrt{\bar\alpha_{t-1}}x_0, (1 - \bar\alpha_{t-1}) \textbf{I})}{\mathcal{N}(x_{t} ; \sqrt{\bar\alpha_{t}}x_0, (1 - \bar\alpha_{t})\textbf{I})} \\ &\propto \mathcal{N}( x_{t-1} ; \underbrace{\frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_{t} + \sqrt{\bar\alpha_{t-1}}(1-\alpha_t)x_0}{1 -\bar\alpha_{t}}}_{\mu_q(x_t, x_0)}, \underbrace{\frac{(1 - \alpha_t)(1 - \bar\alpha_{t-1})}{1 -\bar\alpha_{t}}\textbf{I}}_{{\Sigma}_q(t)}) \end{align} q(xt−1∣xt,x0)=q(xt∣x0)q(xt∣xt−1,x0)q(xt−1∣x0)=N(xt;αˉtx0,(1−αˉt)I)N(xt;αtxt−1,(1−αt)I)N(xt−1;αˉt−1x0,(1−αˉt−1)I)∝N(xt−1;μq(xt,x0) 1−αˉtαt(1−αˉt−1)xt+αˉt−1(1−αt)x0,Σq(t) 1−αˉt(1−αt)(1−αˉt−1)I)
通过上面的公式,我们可以知道,当知道 x 0 x_0 x0 和 x t x_t xt, 既可以得到 x t − 1 x_{t-1} xt−1. 但是, 我们没有办法获取真实的 x 0 x_0 x0, 所以只能估计 x t x_t xt 对应的 x ^ 0 \hat{x}_0 x^0 是什么样子的。
μ q ( x t , x 0 ) = α t ( 1 − α ˉ t − 1 ) x t + α ˉ t − 1 ( 1 − α t ) x 0 1 − α ˉ t Σ q ( t ) = ( 1 − α t ) ( 1 − α ˉ t − 1 ) 1 − α ˉ t I \begin{align} \mu_q(x_t, x_0) &= \frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})x_{t} + \sqrt{\bar\alpha_{t-1}}(1-\alpha_t)x_0}{1 -\bar\alpha_{t}} \\ {\Sigma}_q(t) &= \frac{(1 - \alpha_t)(1 - \bar\alpha_{t-1})}{1 -\bar\alpha_{t}}\textbf{I} \end{align} μq(xt,x0)Σq(t)=1−αˉtαt(1−αˉt−1)xt+αˉt−1(1−αt)x0=1−αˉt(1−αt)(1−αˉt−1)I
- 第一种: 先利用预测的噪声 ϵ t \epsilon_t ϵt 估计 x ^ 0 \hat{x}_0 x^0. 然后利用 x t x_t xt 和 x ^ 0 \hat{x}_0 x^0 估计 x t − 1 x_{t-1} xt−1
x ^ 0 t − 1 = x t − 1 − α ˉ t ⋅ ϵ θ ( x t , t ) α ˉ t \begin{align} \hat{x}_0^{t-1} &= \frac{ x_t - \sqrt{1-\bar{\alpha}_t} \cdot \epsilon_{\theta}(x_t, t) }{ \sqrt{\bar{\alpha}_t} } \end{align} x^0t−1=αˉtxt−1−αˉt⋅ϵθ(xt,t)
x ^ 0 t − 1 \hat{x}_0^{t-1} x^0t−1 表示第 t − 1 t-1 t−1时刻估计的 x 0 x_0 x0. 基本上,在采样一半时,基本上预测的 x 0 x_0 x0 就和真实图片差不多了.
接下来计算 x t − 1 x_{t-1} xt−1 的均值和方差. 方差非常重要,不能忽略
m e a n ( x t − 1 ) = α t ( 1 − α ˉ t − 1 ) 1 − α ˉ t ⋅ x t + α ˉ t − 1 ( 1 − α t ) 1 − α ˉ t ⋅ x ^ 0 t − 1 v a r ( x t − 1 ) = ( 1 − α t ) ( 1 − α ˉ t − 1 ) 1 − α ˉ t ⋅ I x t − 1 = m e a n ( x t − 1 ) + v a r ( x t − 1 ) \begin{align} \mathrm{mean}(x_{t-1}) &= \frac{ \sqrt{\alpha_t}(1-\bar{\alpha}_{t-1}) }{ 1-\bar{\alpha}_{t} } \cdot x_t + \frac{ \sqrt{\bar{\alpha}_{t-1}}(1-\alpha_t) }{ 1-\bar{\alpha}_{t} } \cdot \hat{x}_0^{t-1} \\ \mathrm{var}(x_{t-1}) &= \frac{(1 - \alpha_t)(1 - \bar\alpha_{t-1})}{1 -\bar\alpha_{t}} \cdot \textbf{I} \\ x_{t-1} &= \mathrm{mean}(x_{t-1}) + \mathrm{var}(x_{t-1}) \end{align} mean(xt−1)var(xt−1)xt−1=1−αˉtαt(1−αˉt−1)⋅xt+1−αˉtαˉt−1(1−αt)⋅x^0t−1=1−αˉt(1−αt)(1−αˉt−1)⋅I=mean(xt−1)+var(xt−1)
for i, t in enumerate(ddpm_scheduler.timesteps):alpha_t = alphas[t] alpha_t_bar = alphas_cumprod[t]alpha_t_bar_prev = alphas_cumprod[t - 1] if t - 1 >= 0 else torch.tensor(1.0)# -------------## 1. x_0 和 x_t的系数pred_ori_sample_coeff = torch.sqrt(alpha_t_bar_prev) * (1-alpha_t) / (1-alpha_t_bar)current_sample_coeff = torch.sqrt(alpha_t) * (1-alpha_t_bar_prev) / (1-alpha_t_bar)## 2. 预测 x_0noise_pred = ddpm_noise_model(x_t, t)['sample']est_x_0 = (x_t - torch.sqrt(1-alpha_t_bar) * noise_pred) / torch.sqrt(alpha_t_bar)## 3. clip x_0est_x_0 = est_x_0.clamp(-1, 1)## 4. 预测 x_{t-1}x_t_prev = pred_ori_sample_coeff * est_x_0 + current_sample_coeff * x_t## 5. 添加噪声if t > 0:std_var_noise = torch.randn_like(x_t).to(device)x_t_var_coeff = (1-alpha_t) * (1-alpha_t_bar_prev) / (1-alpha_t_bar)x_t_var_coeff = torch.sqrt(x_t_var_coeff)x_t_prev = x_t_prev + x_t_var_coeff * std_var_noisex_t = x_t_prev