无人船 | 图解基于LQR控制的路径跟踪算法(以全驱动无人艇WAMV为例)

1 最优控制线性二次型问题

最优控制理论是一种数学和工程领域的理论，旨在寻找如何使系统在给定约束条件下达到最佳性能的方法。它的基本思想是通过选择合适的控制输入，以最小化或最大化某个性能指标来优化系统的行为。其中，系统的动态行为通常用状态方程描述，状态表示系统在某一时刻的内部状态。状态空间表示将系统的状态和控制输入表示为向量，通常用微分方程或差分方程来描述系统的演化。在最优控制理论中，会设置代价函数或者目标函数，用来衡量系统行为的好坏的函数。性能指标可以是各种形式，如最小化路径长度、最小化能量消耗、最大化系统稳定性等。最优控制理论在许多领域都有广泛的应用，包括航空航天、机器人学、经济学、生态学等。

若系统动力学特性可以用一组线性微分方程表示，且性能指标为状态变量和控制变量的二次型函数，则此类最优控制问题称为线性二次型问题。线性二次调节器(Linear Quadratic Regulator, LQR)是求解线性二次型问题常用的求解方法之一，其假设系统零输入且期望状态为零。

如图所示的全状态反馈控制系统。设控制误差${\mathbf{x}}_k={\mathbf{z}}_k-{\mathbf{z}}_k^{\ast }$，其中${\mathbf{z}}_k$、${\mathbf{z}}_k^{\ast }$分别是第$k$个控制时间步的实际状态和期望状态，则全反馈控制律由误差驱动

$${\mathbf{v}}_k={\mathbf{v}}_k^{\ast }-{\mathbf{K}\mathbf{x}}_k\stackrel{\mathbf{u}=\mathbf{v}-{\mathbf{v}}^{\ast }}{\iff }{\mathbf{u}}_k=-{\mathbf{K}\mathbf{x}}_k$$

上式表明可以通过选取状态变量和输入变量，使系统等效为零输入(跟踪期望输入)且期望状态为零(消除状态误差)，满足应用LQR进行最优控制的条件。定义代价函数

$$J=\sum _{k=0}^N\left({\mathbf{x}}_k^T{\mathbf{Q}\mathbf{x}}_k+{\mathbf{u}}_k^T{\mathbf{R}\mathbf{u}}_k\right)$$

其中$\mathbf{Q}$与$\mathbf{R}$是用户设定的半正定矩阵，前者衡量了系统状态向期望轨迹的收敛速度，后者衡量了系统能量消耗的相对大小，二者互相制约——希望系统快速收敛往往需要加强控制力度，导致能量耗散。因此， 与 需要结合具体场景进行调节。

2 LQR的价值迭代推导

针对$J$进行优化，引入价值迭代策略，价值迭代的理论基础请看Pytorch深度强化学习1-4：策略改进定理与贝尔曼最优方程详细推导

$$J_k\left({\mathbf{x}}_k,{\mathbf{u}}_k\right)=\underset{{\mathbf{u}}_k}{\min }\left[{\mathbf{x}}_k^T{\mathbf{Q}\mathbf{x}}_k+{\mathbf{u}}_k^T{\mathbf{R}\mathbf{u}}_k+J_{k+1}\left({\mathbf{x}}_{k+1}\right)\right]$$

即第$k$步到终端的代价等于当前步的代价与第$k+1$步到终端的代价之和。根据$J$的定义，其一定能表示成二次型$J_k={\mathbf{x}}_k^T{\mathbf{P}}_k{\mathbf{x}}_k$，对于优化问题${\mathbf{u}}_k=\mathrm{a}\mathrm{r}\mathrm{g}{\min }_{{\mathbf{u}}_k}{J}_k\left({\mathbf{x}}_k,{\mathbf{u}}_k\right)$，令

$$\begin{array}{rl}\frac{\partial J_k\left({\mathbf{x}}_k,{\mathbf{u}}_k\right)}{\partial {\mathbf{u}}_k}& =\frac{\partial }{\partial {\mathbf{u}}_k}\left({\mathbf{x}}_k^T{\mathbf{P}}_k{\mathbf{x}}_k+{\mathbf{u}}_k^T{\mathbf{R}\mathbf{u}}_k+J_{k+1}\left({\mathbf{A}\mathbf{x}}_k+{\mathbf{B}\mathbf{u}}_k\right)\right)\\ & =\frac{\partial }{\partial {\mathbf{u}}_k}\left({\mathbf{u}}_k^T{\mathbf{R}\mathbf{u}}_k+{\left({\mathbf{A}\mathbf{x}}_k+{\mathbf{B}\mathbf{u}}_k\right)}^T{\mathbf{P}}_{k+1}\left({\mathbf{A}\mathbf{x}}_k+{\mathbf{B}\mathbf{u}}_k\right)\right)\\ & =2\left(\mathbf{R}+{\mathbf{B}}^T{\mathbf{P}}_{k+1}\mathbf{B}\right){\mathbf{u}}_k+2{\mathbf{B}}^T{\mathbf{P}}_{k+1}{\mathbf{A}\mathbf{x}}_k\\ & =0\end{array}$$

则${\mathbf{u}}_k^{\ast }=-{\left(\mathbf{R}+{\mathbf{B}}^T{\mathbf{P}}_{k+1}\mathbf{B}\right)}^{-1}{\mathbf{B}}^T{\mathbf{P}}_{k+1}{\mathbf{A}\mathbf{x}}_k$，对比${\mathbf{u}}_k=-{\mathbf{K}\mathbf{x}}_k$可得

$${\mathbf{K}}_k={\left(\mathbf{R}+{\mathbf{B}}^T{\mathbf{P}}_{k+1}\mathbf{B}\right)}^{-1}{\mathbf{B}}^T{\mathbf{P}}_{k+1}\mathbf{A}$$

将${\mathbf{u}}_k=-{\mathbf{K}\mathbf{x}}_k$代入$J_k$可得

$$J_k={\mathbf{x}}_k^T{\mathbf{P}}_k{\mathbf{x}}_k={\mathbf{x}}_k^T\left(\mathbf{Q}+{\mathbf{K}}_k^T{\mathbf{R}\mathbf{K}}_k+\left(\mathbf{A}-{\mathbf{B}\mathbf{K}}_k\right){\mathbf{P}}_{k+1}\left(\mathbf{A}-{\mathbf{B}\mathbf{K}}_k\right)\right){\mathbf{x}}_k$$

从而

$${\mathbf{P}}_k=\mathbf{Q}+{\mathbf{A}}^T{\mathbf{P}}_{k+1}\mathbf{A}-{\mathbf{A}}^T{\mathbf{P}}_{k+1}\mathbf{B}{\left(\mathbf{R}+{\mathbf{B}}^T{\mathbf{P}}_{k+1}\mathbf{B}\right)}^{-1}{\mathbf{B}}^T{\mathbf{P}}_{k+1}\mathbf{A}$$

称为离散迭代黎卡提方程。根据贝尔曼最优原理，在迭代过程中${\mathbf{P}}_k$会逐步收敛。

3 基于全驱动无人船动力学的LQR

针对WAMV非线性动力学模型，首先将非线性问题线性化，得到系统线性误差状态方程。具体而言，选择状态量$\mathbf{x}={\left[\begin{array}{cccccc}lx& y& \psi & u& v& r\end{array}\right]}^T$和控制量$\mathbf{u}={\left[\begin{array}{ccc}{\tau }_l& {\tau }_m& {\tau }_r\end{array}\right]}^T$，系统状态方程为$\dot{\mathbf{x}}=\mathbf{f}\left(\mathbf{x},\mathbf{u}\right)$，则令$\mathbf{f}$在参考点${\mathbf{x}}_r$、${\mathbf{u}}_r$泰勒级数展开，忽略非线性项可得

$$\dot{\mathbf{x}}=\mathbf{f}\left({\mathbf{x}}_r,{\mathbf{u}}_r\right)+\frac{\partial \mathbf{f}\left(\mathbf{x},\mathbf{u}\right)}{\partial \mathbf{x}}{\mid }_{{\mathbf{x}}_r,{\mathbf{u}}_r}^{}\left(\mathbf{x}-{\mathbf{x}}_r\right)+\frac{\partial \mathbf{f}\left(\mathbf{x},\mathbf{u}\right)}{\partial \mathbf{u}}{\mid }_{{\mathbf{x}}_r,{\mathbf{u}}_r}^{}\left(\mathbf{u}-{\mathbf{u}}_r\right)$$

其中雅克比矩阵

$$\{\begin{array}{l}\mathbf{A}=\frac{\partial \mathbf{f}\left(\mathbf{x},\mathbf{u}\right)}{\partial \mathbf{x}}{\mid }_{{\mathbf{x}}_r,{\mathbf{u}}_r}^{}=\left[\begin{array}{cccccc}0& 0& -u_r\sin {\psi }_r-v_r\cos {\psi }_r& \cos {\psi }_r& -\sin {\psi }_r& 0\\ 0& 0& u_r\cos {\psi }_r-v_r\sin {\psi }_r& \sin {\psi }_r& \cos {\psi }_r& 0\\ 0& 0& 0& 0& 0& 1\\ 0& 0& 0& \frac{X_u+2X_{|u|u}|u_r|}{m}& r_r& v_r\\ 0& 0& 0& -r_r& Y_v/m& -u_r\\ 0& 0& 0& 0& 0& N_r/I_z\end{array}\right]\\ \mathbf{B}=\frac{\partial \mathbf{f}\left(\mathbf{x},\mathbf{u}\right)}{\partial \mathbf{u}}{\mid }_{{\mathbf{x}}_r,{\mathbf{u}}_r}^{}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\\ 1/m& 0& 1/m\\ 0& 1/m& 0\\ -D/I_z& 0& D/I_z\end{array}\right]\end{array}$$

选择状态误差量$\tilde{\mathbf{x}}={\left[\begin{array}{cccccc}lx-x_r& y-y_r& \psi -{\psi }_r& u-u_r& v-v_r& r-r_r\end{array}\right]}^T$得到线性误差状态方程$\dot{\tilde{\mathbf{x}}}=\mathbf{A}\tilde{\mathbf{x}}+\mathbf{B}\mathbf{u}+\mathbf{C}$，其中$\mathbf{C}={\mathbf{B}\mathbf{u}}_r$是常数矩阵。为了应用标准LQR过程，暂时忽略常数$\mathbf{C}$，采用采样步长为$T$的前向欧拉法离散化上述状态方程可得

$$\tilde{\mathbf{x}}\left(k+1\right)=\left(T\mathbf{A}+\mathbf{I}\right)\tilde{\mathbf{x}}\left(k\right)+T\mathbf{B}\mathbf{u}\left(k\right)$$

接着进行LQR过程即可

4 跟踪效果分析

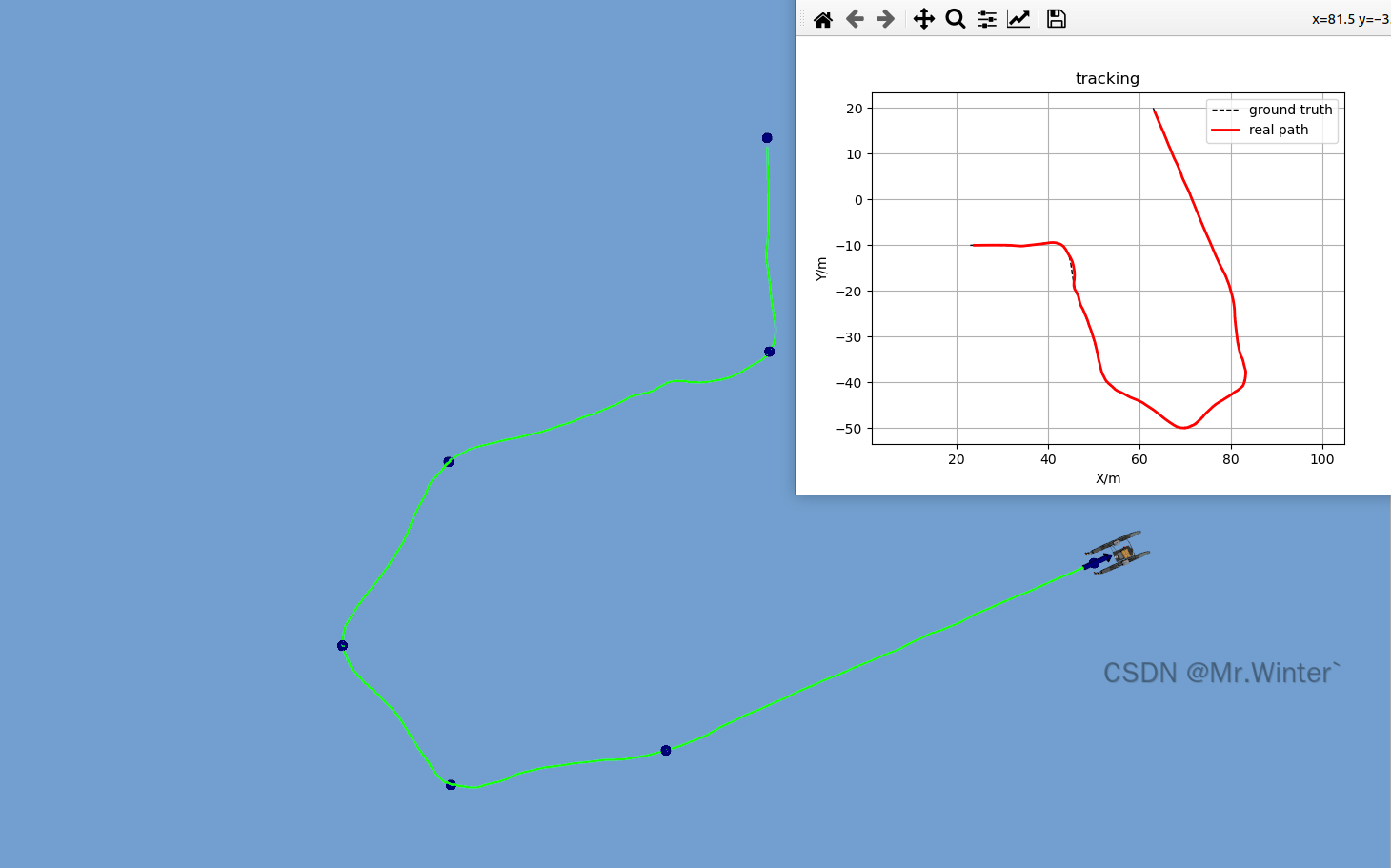
定性测试结果：

在考虑水动力、风力等真实干扰的情况下，跟踪轨迹如下所示，定量测试结果为：

• 平均跟踪误差：0.188978 m
• 最大跟踪误差：0.626185 m
• 最小跟踪误差：0.006301 m

---

🔥 更多精彩专栏：

• 《ROS从入门到精通》
• 《Pytorch深度学习实战》
• 《机器学习强基计划》
• 《运动规划实战精讲》
• …

👇源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系👇