动态规划中处理边界条件的常见策略
动态规划是一种常见的算法设计技巧,通常用于解决具有最优子结构和重叠子问题性质的问题。在使用动态规划时,边界条件的处理通常是关键步骤,因为动态规划表格的初始值将直接影响后续的计算结果。本文将详细阐述边界条件处理的策略,并通过代码示例以增强理解。
一、边界条件的重要性
边界条件是指动态规划过程中涉及的最小问题或初始状态的处理。这些条件为整个动态规划的计算提供了基础。如果边界条件不正确或没有设置,最终的结果可能会出错。
1. 确定初始状态
在动态规划中,初始状态通常是表格的第一行或第一列。这些状态的值需要直观地表达出从起点到达这些状态的最小代价。
二、处理边界条件的常见策略
1. 线性递归初始化
当问题的边界条件可以通过一系列简单的线性递归关系得出时,可以直接用循环初始化边界。
示例:最小路径和
考虑一个不规则的二维网格,需要计算从左上角到右下角的最小路径和。可以使用动态规划来解决这个问题。
Java 代码实例
class Solution {public int minPathSum(int[][] grid) {int m = grid.length; // 行数int n = grid[0].length; // 列数// 创建 dp 数组int[][] dp = new int[m][n];// 初始化第一行dp[0][0] = grid[0][0]; // 起点for (int j = 1; j < n; j++) {dp[0][j] = dp[0][j - 1] + grid[0][j]; // 从左到右累加}// 初始化第一列for (int i = 1; i < m; i++) {dp[i][0] = dp[i - 1][0] + grid[i][0]; // 从上到下累加}// 填充 dp 数组for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];}}return dp[m - 1][n - 1]; // 返回右下角元素}
}
2. 递归构造动态表格
在某些情况下,可以根据问题的定义递归地构建动态规划表格,以便对其进行初始化。
示例:斐波那契数列
斐波那契数列可以用动态规划生成,初始化只需设定前两个数字。
Java 代码实例
class Solution {public int fib(int n) {if (n == 0) return 0;if (n == 1) return 1;int[] dp = new int[n + 1];dp[0] = 0; // F(0)dp[1] = 1; // F(1)for (int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2]; // 状态转移}return dp[n]; // 返回 F(n)}
}
3. 处理特殊情况
在处理边界条件时,确保代码能够正确处理特殊情况是非常重要的。有时,特殊情况可能会影响边界值的初始化或最终的状态转移。
示例:最长递增子序列
在求解最长递增子序列(LIS)的动态规划中,需要处理特殊情况(如空数组)。
Java 代码实例
class Solution {public int lengthOfLIS(int[] nums) {if (nums.length == 0) return 0;int[] dp = new int[nums.length];int maxLength = 1;for (int i = 0; i < nums.length; i++) {dp[i] = 1; // 初始化每个位置的 LIS 为 1for (int j = 0; j < i; j++) {if (nums[i] > nums[j]) {dp[i] = Math.max(dp[i], dp[j] + 1);}}maxLength = Math.max(maxLength, dp[i]);}return maxLength; // 返回最大 LIS}
}
4. 合理利用空间
在某些情况下,如果问题只依赖于前一步或前几步的状态,可以合理利用空间,减少不必要的内存开销。
示例:爬楼梯
在爬楼梯的问题中,当前状态只与前两步有关。
Java 代码实例
class Solution {public int climbStairs(int n) {if (n <= 2) return n; // 特殊情况int first = 1, second = 2;for (int i = 3; i <= n; i++) {int current = first + second; // 当前步数first = second; // 更新前一阶梯second = current; // 更新当前阶梯}return second; // 返回最终结果}
}
三、总结
边界条件的处理在动态规划中具有重要意义,尤其是在搭建状态转移表格时。合理的初始化边界条件能够确保我们后续计算的正确性。通过示例,您可以看到在不同情况下如何灵活处理这些边界条件,以确保算法的高效性和准确性。动态规划不仅仅是一个强大的算法设计工具,也是建立在正确的逻辑和基础上的,我们需要花时间仔细设计和验证每个步骤。
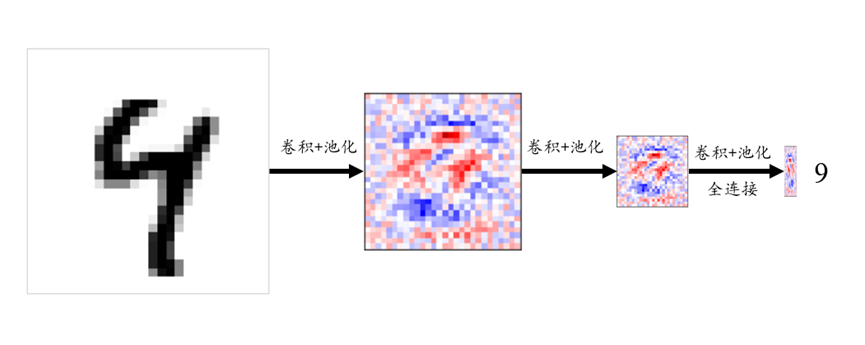










![[阻塞队列]](https://i-blog.csdnimg.cn/direct/c0e711d9bbc14145a74353c2a7649747.jpeg)



![[ComfyUI]Flux:繁荣生态魔盒已开启,6款LORA已来,更有MJ6写实动漫风景艺术迪士尼全套](https://img-blog.csdnimg.cn/direct/4a2d3a791f754642af3f0383c95ee9c7.png#pic_center)

