1、前缀和
- 对于一个给定的数组A,它的前缀和数列S是通过递推求得的:
//A[]和S[]的有效数据从下标1开始,方便后续计算 s[0] = 0; for (int i = 1; i <= n; i++) {s[i] = s[i - 1] + A[i]; }- 作用:用于快速求得某一部分的和:对于一个部分和,即数列A某个下标区间内的数的和,可以表示为前缀和相减的形式:
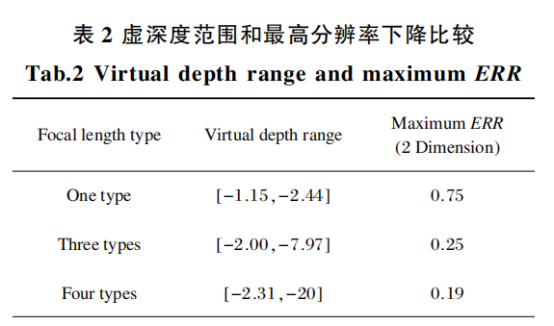
- 在二维数组中,S[ i,j ]表示A数组的前缀和:
,递推公式为:
memset(S,0,sizeof(S)); for (int i = 1; i <= n; i++)for(int j = 1; j <= n; j++){S[i][j] = S[i - 1][j] + S[i][j - 1] - S[i - 1][j - 1] + A[i][j];}- 作用:用于快速求得某一部分二维数组的和:对于二维数组的一部分和,即对于任意一个边长为R1,R2的矩阵的和,有:
1.1 题目--激光炸弹
99. 激光炸弹 - AcWing题库
思路:
- 计算价值的前缀和
- 根据炸弹R*R的范围由前缀和计算
- 时间复杂度O(N^2)
#include <iostream> #include <cstring> #include <cstdlib> #include <algorithm> using namespace std; typedef pair<int,int> PII;const int N = 5010; int n, r; int sum[N][N]; PII max_xy = {1,1}; int res;int main() {cin >> n >> r;//炸弹范围超过最大边界,直接计算5001以内的就行了 r = min(r, 5001);max_xy.first = max_xy.second = r;while(n--){int x,y,w;cin >> x >> y >> w;//加1是因为从{1,1}开始x += 1, y += 1;sum[x][y] += w;if(x > max_xy.first)max_xy.first = x;if(y > max_xy.second)max_xy.second = y;}//前缀和for(int i = 1; i <= max_xy.first; i++)for(int j = 1; j <= max_xy.second; j++)sum[i][j] += sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1];//求最大价值//每次枚举的都是r*r正方形的右下角,所以从r开始for (int i = r; i <= max_xy.first; i++)for(int j = r; j <= max_xy.second; j++)res = max(res, sum[i][j] - sum[i - r][j] - sum[i][j - r] + sum[i - r][j - r]); cout << res << endl;return 0; }
2、差分
- 对于一个给定的数列A,它的差分数列B定义为:
- 易发现前缀和和差分是一对互逆运算,差分数组的前缀和就是原数列A,前缀和序列S的差分数组的差分也是原序列A。
- 作用:给序列A的区间[ l,r ]所有数快速加上d,即:
通过差分数组的O(1)复杂度操作下,对差分数组求前缀和得到的序列就是序列A在指定[ l,r ]区域中所有数加上d。
2.1 题目--增减序列
100. 增减序列 - AcWing题库
思路:
- 通过原序列a求出差分序列b,令
- 目标是将原序列a所有数相等,等价于差分序列b中,b2、b3...bn全变为0(b1不需要为0,因为b1=a1)
- 每次对原序列a[ l,r ]区间内+1/-1,等价于在差分序列中,选择
或
- 从b1,b2,b3...bn中任选两个数的方法可分为4类:
a、选bi和bj,其中2 <= i,j <= n,保证bi和bj一正一负的情况下,尽量多采取这个操作,可以快速将bi和bj接近0
b、没有a的情况时,选b1和bj,其中 2 <= j <= n
c、没有a的情况时,选bi和bn+1,其中 2 <= i <= n
d、选b1和bn+1没有意义,会使原序列a全体+1/-1,浪费了一次操作- 设b2、b3、b4...bn中正数总和为p,负数总和的绝对值为q。首先以正负数配对为主要方式,可以执行min(p,q)次;剩下的|p-q|次需要与b1或bn+1进行配对(即执行b或操作)。总的执行次数为:min(p,q) + |p - q| = max(p,q)次。
- 结果个数可以通过判断b1的不同值的个数来得出,b1的结果为|p-q| + 1,都是|p-q|次操作的结果,+1是存在结果b1没有进行配对;最终结果个数为|p-q| + 1
#include <iostream> #include <algorithm> using namespace std;const int N = 1e5 + 10; int b[N];int main() {int n;cin >> n;int cur;int per;cin >> cur;b[1] = cur,per = cur;long long p = 0, q = 0; //p表示正数之和,q表示负数绝对值之和for (int i = 2; i <= n; i++){cin >> cur;b[i] = cur - per;per = cur;if(b[i] >= 0)p += b[i];elseq -= b[i];} cout << max(p,q) << endl;cout << abs(p-q) + 1 << endl;return 0; }
2.2 题目-- Tallest Cow
有N头牛站成一行。两头牛能够相互看见,当且仅当它们中间的牛身高都比它们矮。现在,我们只知道其中最高的牛是第P头,它的身高是H,不知道剩余N-1头牛的身高。但是,我们还知道M对关系,每对关系都指明了某两头牛Ai和Bi可以相互看见。求每头牛的身高最大可能是多少。
数据范围:1≤N,M≤10^4,1≤H≤10^6。
思路:初始化一个数组全为0表示牛的相对高度,假如有一对关系a和b位置的牛可以互相看到,那么就将a+1,a+2...b-2,b+1的位置全部减去1,就表示a和b之间的牛都比a和b之间的相对高度少1(为什么减1,为了保证每头牛高度最大)。第P头牛是最高的,所以b[p] = 0,所以最后得到的相对高度加上H就是绝对高度。数组减1的操作可以使用差分来降低时间复杂度。
#include <iostream> #include <map> using namespace std;const int N = 10010; map<pair<int,int>,bool> existed; int c[N],d[N];int main() {int n,p,h,m;cin >> n >> p >> h >> m;for(int i = 1; i <= m; i++){int a, b;cin >> a >> b;if(a > b) swap(a,b);if(existed[{a,b}]) continue;//可能会有一条关系重复输入的情况d[a+1]--,d[b]++;existed[{a,b}] = true;}//差分数组求前缀和得到目标序列for(int i = 1; i <= n; i++){c[i] = c[i - 1] + d[i];cout << c[i] + h << ' ';}cout << endl;return 0; }