关于圆周率-4

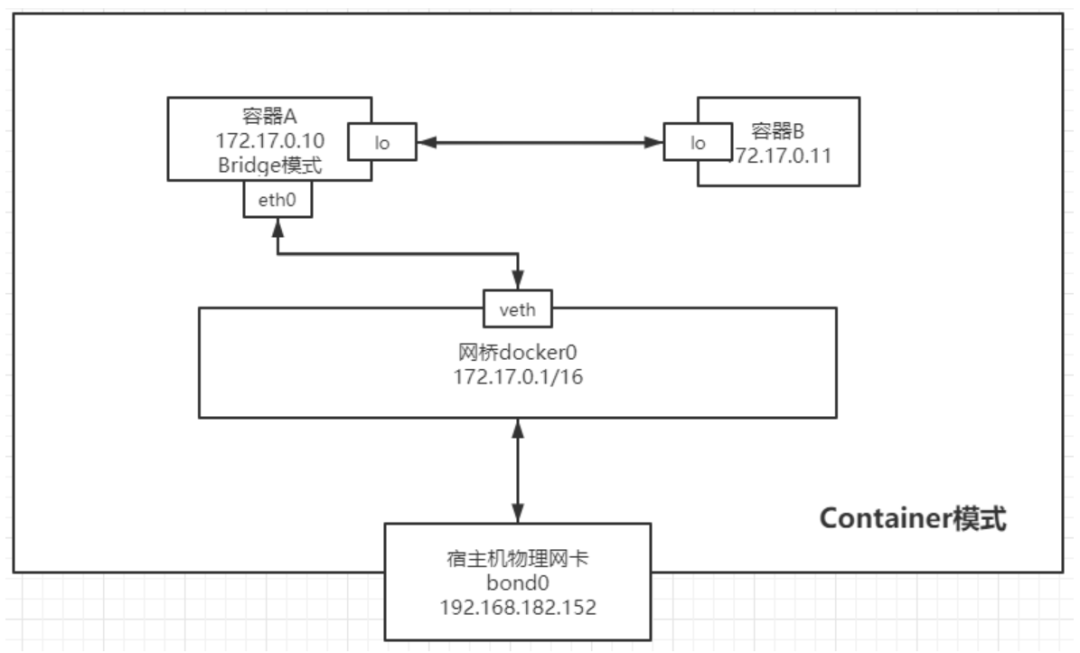
在这里总结一下，以上分析，都是基于“单位”的。计算圆周率的时候，我们考虑的是做一个单位来理解，而它的倍数则作为某种比例缩放来理解。同理欧拉函数，也是用弧长来作为单位的，其它弧长则是基于这个单位的比例缩放来理解的。若是不从单位去理解，而假定1为单位，那么像是

中多个相乘的情况就无法解释了。所以，首先出现的是，

然后才是

在这一类问题上，1不是单位，以及才是，这是非常反直觉的认识。

回到问题本身，要知道我们现在讨论的是一个数，它很大，是观察者所提供的虚数单位的若干倍甚至若干次方，但是它体现出来的却不是一个数，而是具有三个分量的向量。这三个向量可以构造一个三维空间的基。不难想到，如果这个数本身或者是观察者提供的虚数单位发生变化，这个结构也会随之变动。而这种变动若能保持某种规律，观察的结果就完全可能是一个在复平面中旋转的圆周运动，或者在复空间中旋进的螺线。

而这只需要观察者或者所观之物其一（或者两者共同）出现数量上的变更而已。我们假定观察者自身不变，所观之物，也就是这个数不断增长（也可以认为是所观之物的增长快于观察者的增长），增长或者负增长都可以，那么我们在这样一个三维空间之中就会看到一条不断旋转前进的螺线。

举一个具体的例子，你认为地球围绕太阳转吗？当然如此。但是，从上述角度来说，也可以认为它并没有围绕任何东西旋转，只是承载它的空间，在增长而已。至于太阳对地球的引力，也可以仅仅认为是空间增长的速率，靠近太阳的和远离太阳的不同，而地球所在空间最终选择了一种速度，以平衡和适应太阳周边空间增长的速度而已。我们把地球想象为一个质点，太阳是一个质量更大的质点。

我们暂时不考虑太阳巨大的质量产生引力的问题，这超过了当前讨论的范围。只考虑地球绕着太阳转的事实。我们把太阳当作指数螺线的中心，那么距离太阳为的轨道上，我们就可以认为那个轨道上布满了振动，而那些振动就是一大堆都具有，

形式的“数”在增长的过程。那些“数”不必在那个轨道上，或者说无所谓在哪，而那些数，用为虚数单位去观察，它们就构成了轨道。它们也根本无需“旋转”，只是因为不同圈层的旋转速率不同，而显示出切向上的相对运动。那些个“数”，就构成了那个圈层的空间，或者说轨道。而那些不同圈层的数，就构成了太阳周围的整个空间，或者说所有的轨道。地球在地球的轨道上，也就是说，它被那个空间承载着，或者和那个轨道所对应的空间能够进行交互。既然运动只是一个不断增长的过程，那么很自然的，增长就一定会达到某一个程度，而那个程度的数量，对于具有无限可能性的宇宙来说，也显然是存在的。就像随着数列长度的增加，等差数列或者等比数列，一定会超过某个极限，而那个极限数量显然也必须是存在的，因为一切数量都是存在的。

若是增长还没有到达那个数量，就只是时候不到而已。而那个数量，在前面的讨论中已经说过，它就是三维空间的某个位置。所以说，太阳周围的振动圈层，承载并和地球交互，直到振动增长达到某个数量，而那个数量显然也是存在的，只是目前还没有到达而已。

既然虚数单位可以表示一个极大的数（超出可数范围），那么它的倒数就可以表示一个很小的数（被认为是0）。考虑，

这个数，它也可以写成，

这里就成为某种单位，比如我们认为它指的是时间单位，那么这个指的就是我们可以区分的最小时间单位，而那个更大的i导致的更小的都被认为是一样的。由此来说，不管怎么变化，

也就是一个周期的长度（的对数）都等于4，所以这样的话，我们就用这种结构同时获得了最小单位时间和单位长度，最小单位时间就是我们选择的，单位长度，我们指的是在z方向上的单位长度（取对数），它就是4；而完成一个最小单位时间对应的长度（取对数）就是四分之一个单位长度，也就是1。最小的单位时间，不变的单位长度，两者相比，我们就得到了最大的单位速度，也就是说，这个速度就是，

如果不取对数，那么四分之一周期完成的长度就是本身，结果就是，

不难发现，这就是数学意义上的光速。在z方向上完成单位长度1（或者），用时为最小时间，这个结果就是光速。同样的单位长度，若是用时更少，也因为更大的虚数单位和这个最大的虚数单位不可区分，它的倒数也无法更小，所以结果的速度，就不可能超过这个极限。所有超过这个极限的长度和时间的比值，最终都会被认为就是这个极限。由此来说，并不是没有超光速，而是超光速的，被虚数单位的周期性效果屏蔽了。更大的虚数单位体现为更大的结构，而不是速度。