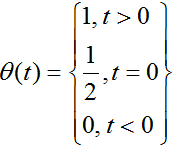【AtCoder】Beginner Contest 377-C.Avoid Knight Attack

Avoid Knight Attack

题目链接

Problem Statement

There is a grid of $N^2$ squares with $N$ rows and $N$ columns. Let $(i, j)$ denote the square at the $i$ -th row from the top $(1\leq i\leq N)$ and $j$ -th column from the left $(1\leq j\leq N)$ .

Each square is either empty or has a piece placed on it. There are $M$ pieces placed on the grid, and the $k$ -th $(1\leq k\leq M)$ piece is placed on square $a_k,b_k)$ .

You want to place your piece on an empty square in such a way that it cannot be captured by any of the existing pieces.

A piece placed on square $(i, j)$ can capture pieces that satisfy any of the following conditions:

Placed on square $(i + 2, j + 1)$
Placed on square $(i + 1, j + 2)$
Placed on square $(i - 1, j + 2)$
Placed on square $(i - 2, j + 1)$
Placed on square $(i - 2, j - 1)$
Placed on square $(i - 1, j - 2)$
Placed on square $(i + 1, j - 2)$
Placed on square $(i + 2, j - 1)$

Here, conditions involving non-existent squares are considered to never be satisfied.

For example, a piece placed on square $(4, 4)$ can capture pieces placed on the squares shown in blue in the following figure:

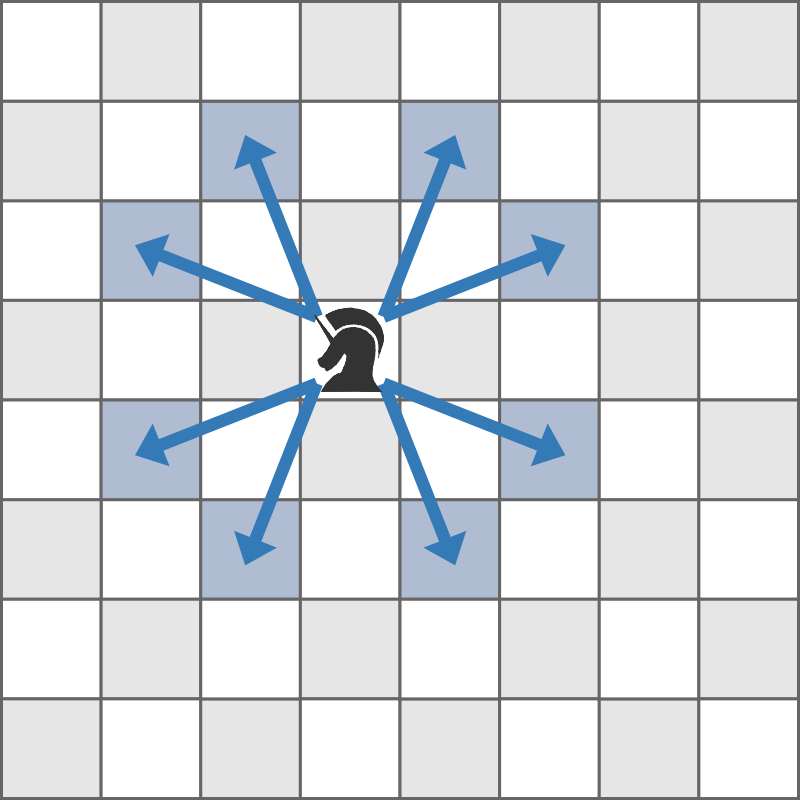
How many squares can you place your piece on?

中文题意

问题陈述

有一个由 $N^2$ 个正方形组成的网格，包含 $N$ 行和 $N$ 列。设 $(i, j)$ 表示从上到下第 $i$ 行 $(1\leq i\leq N)$ 和从左到下第 $j$ 列 $(1\leq j\leq N)$ 处的正方形。

每个方块要么是空的，要么上面放着一个棋子。网格上有 $M$ 个棋子， $k$ 第 $(1\leq k\leq M)$ 个棋子放置在 $KaTeX parse error: Expected 'EOF', got '&' at position 4: (a &̲#95; k,b _ \dots$ 方格上。

你想把你的棋子放在一个空的正方形上，这样它就不会被任何现有的棋子所捕获。

放置在 $(i, j)$ 方块上的棋子可以捕获满足以下任何条件的棋子：

放置在 $(i + 2, j + 1)$ 方块上
放置在正方形 $(i + 1, j + 2)$ 上
放置在 $(i - 1, j + 2)$ 方框上
放置在 $(i - 2, j + 1)$ 方块上
放置在 $(i - 2, j - 1)$ 方块上
放置在正方形 $(i - 1, j - 2)$ 上
放置在 $(i + 1, j - 2)$ 方块上
放置在正方形 $(i + 2, j - 1)$ 上

在这里，涉及不存在的正方形的条件被认为永远不满足。

例如，放置在方格 $(4, 4)$ 上的棋子可以捕获放置在下图中蓝色方格上的棋子：

你能把棋子放在几个方格上？

Constraints

$1\leq N\leq10^9$
$1\leq M\leq2\times10^5$
$1\leq a_k\leq N,1\leq b_k\leq N\ (1\leq k\leq M)$
$(a_k,b_k)\neq(a_l,b_l)\ (1\leq k\lt l\leq M)$
All input values are integers.

Input

The input is given from Standard Input in the following format:

$N$ $M$

$a_1$ $b_1$

$a_2$ $b_2$

$\vdots$

$a_M$ $b_M$

Output

Print the number of empty squares where you can place your piece without it being captured by any existing pieces.

Sample Input 1

Sample Output 1

The existing pieces can capture pieces placed on the squares shown in blue in the following figure:

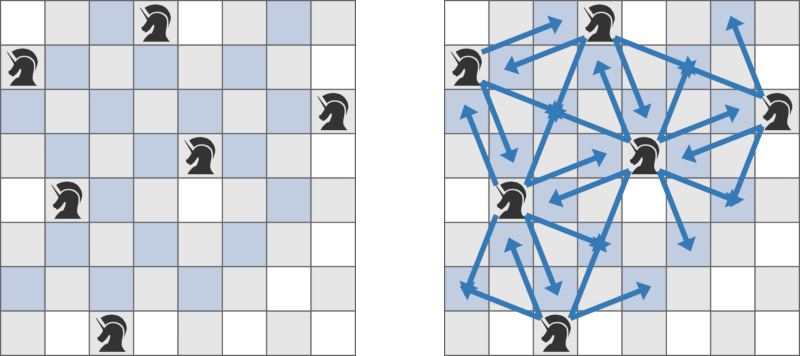
Therefore, you can place your piece on the remaining $38$ squares.

Sample Input 2

1000000000 1
1 1

Sample Output 2

999999999999999997

Out of $10^{18}$ squares, only $3$ squares cannot be used: squares $(1, 1)$ , $(2, 3)$ , and $(3, 2)$ .

Note that the answer may be $2^{32}$ or greater.

Sample Input 3

Sample Output 3

解法

这道题目大意，棋子的攻击位置是一个“日”字型的的走法，如果当前位置上有元素，则“日”字型的位置上都不能放元素。现在要我们统计还有多少个位置可以放元素。

使用八连通日字型分量的形式计算哪个位置不能放棋子，并且使用一个集合将所有不能放棋子的位置存起来。最后使用总的位置个数减去集合的长度就可以判断出有多少个位置还可以放棋子。

因为这道题可用的方格数量高达 $10^{18}$ 个，直接使用二维数组来存的话有可能会爆掉，所以我们使用一个集合来存储已经被占用的下标即可（以数对的形式存储）。

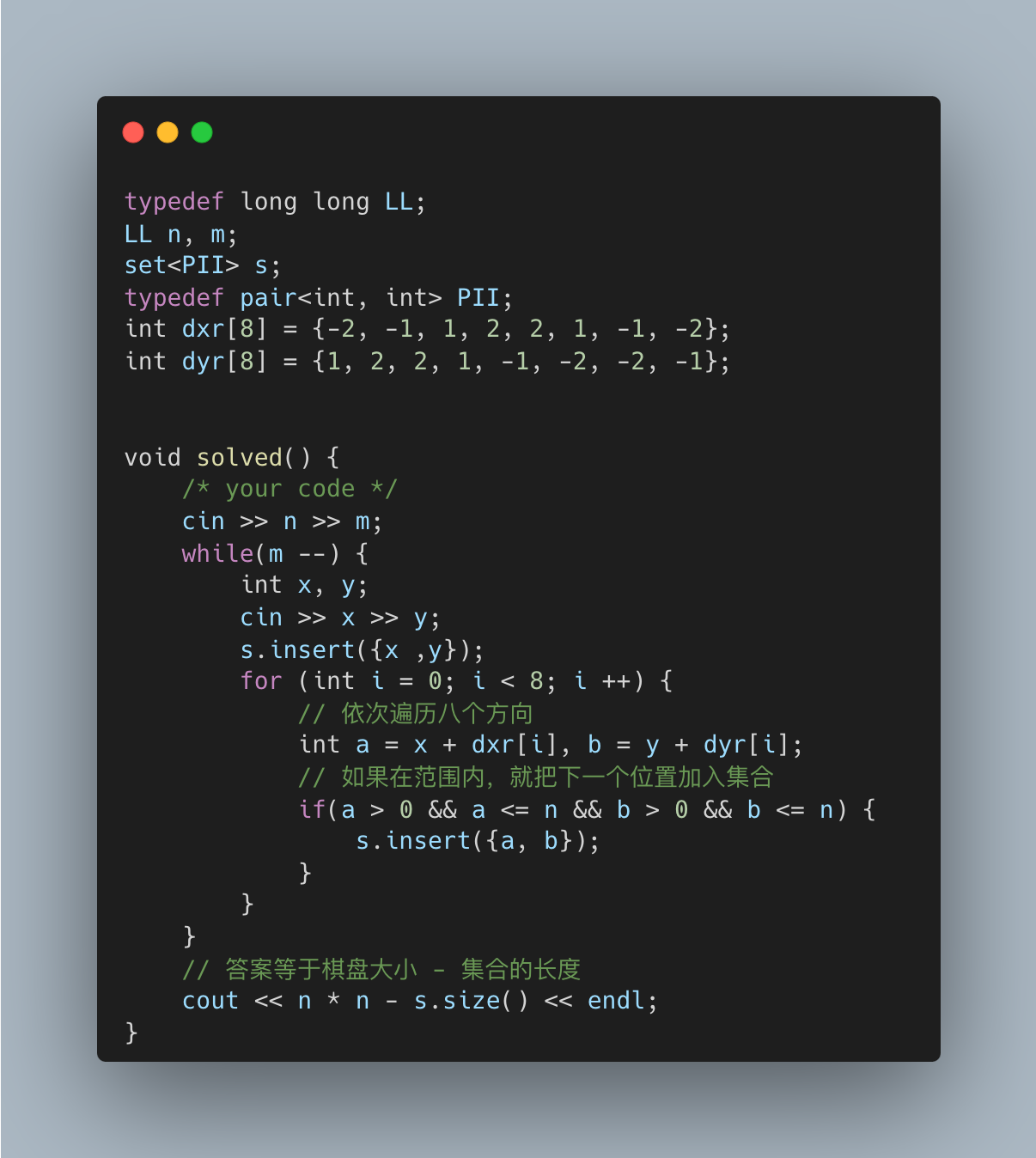
typedef long long LL;
LL n, m;
set<PII> s;
typedef pair<int, int> PII;
int dxr[8] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dyr[8] = {1, 2, 2, 1, -1, -2, -2, -1};void solved() {/* your code */cin >> n >> m;while(m --) {int x, y;cin >> x >> y;s.insert({x ,y});for (int i = 0; i < 8; i ++) {// 依次遍历八个方向int a = x + dxr[i], b = y + dyr[i];// 如果在范围内，就把下一个位置加入集合if(a > 0 && a <= n && b > 0 && b <= n) {s.insert({a, b});}}}// 答案等于棋盘大小 - 集合的长度cout << n * n - s.size() << endl;
}