二叉树中的 路径 被定义为一条节点序列,序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点,且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ,返回其 最大路径和 。
示例 1:

输入:root = [1,2,3] 输出:6 解释:最优路径是 2 -> 1 -> 3 ,路径和为 2 + 1 + 3 = 6
示例 2:
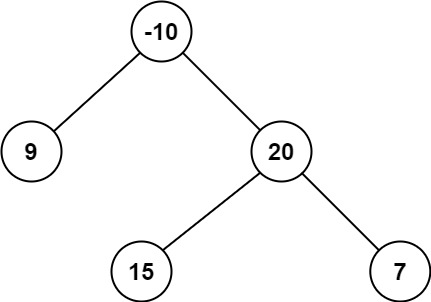
输入:root = [-10,9,20,null,null,15,7] 输出:42 解释:最优路径是 15 -> 20 -> 7 ,路径和为 15 + 20 + 7 = 42
提示:
- 树中节点数目范围是
[1, 3 * 104] -1000 <= Node.val <= 1000
/*** Definition for a binary tree node.* public class TreeNode {* int val;* TreeNode left;* TreeNode right;* TreeNode() {}* TreeNode(int val) { this.val = val; }* TreeNode(int val, TreeNode left, TreeNode right) {* this.val = val;* this.left = left;* this.right = right;* }* */
class Solution {/**对于二叉树的一般问题我想到的都是二叉树的递归套路,对于本题来说看起来也行最大路径和可能出现的三个地方:1. 左树 2. 右树 3.包含根(这里可以认为是只有根或者左右数和根还有左右树经过根跨到对方的所有情况的合集)其实仔细想想就知道只要我们知道左右树的两个信息就能拿下:1.最大路径和 2.以根结尾的最大路径(左右子树的最大路径以根结尾才能和根以及自己的兄弟关联)因为我们找左右子树都要一下这个信息,综合了就是自己的信息 也许这些信息不够,或许我们还需要一个最大路径不包含根的,但是没事我们先试试看,不行再加呗*/public int maxPathSum(TreeNode root) {Info info = getInfo(root);return info.maxPath;}public Info getInfo(TreeNode root) {if(root == null) {return null;}/**如果左右孩子都没有,就返回自己的val作为maxPath和maxPathEndWithRoot */if(root.left == null && root.right == null) {return new Info(root.val, root.val);}/**拿到左右子树的信息*/Info leftInfo = getInfo(root.left);Info rightInfo = getInfo(root.right);/**定义当前节点关于Info的两个信息,暂时设置为自己的val */int maxPath = root.val;int maxPathEndWithRoot = root.val;if(leftInfo != null) {maxPathEndWithRoot = Math.max(maxPathEndWithRoot, leftInfo.maxPathEndWithRoot + root.val);maxPath = Math.max(maxPath, Math.max(leftInfo.maxPath, root.val + leftInfo.maxPathEndWithRoot));}if(rightInfo != null) {maxPathEndWithRoot = Math.max(maxPathEndWithRoot, rightInfo.maxPathEndWithRoot + root.val);maxPath = Math.max(maxPath, Math.max(rightInfo.maxPath, root.val + rightInfo.maxPathEndWithRoot));}/**最大路径还可以是跨越左右树的 */maxPath = Math.max(maxPath, (leftInfo != null && leftInfo.maxPathEndWithRoot>0? leftInfo.maxPathEndWithRoot : 0) + (rightInfo != null && rightInfo.maxPathEndWithRoot>0? rightInfo.maxPathEndWithRoot : 0) + root.val);return new Info(maxPath, maxPathEndWithRoot);}static class Info {int maxPath;int maxPathEndWithRoot;public Info(int maxPath, int maxPathEndWithRoot) {this.maxPath = maxPath;this.maxPathEndWithRoot = maxPathEndWithRoot;}}
}