文章目录
- week 63 GCN-CNNGA
- 摘要
- Abstract
- 1. 题目
- 2. Abstract
- 3. 文献解读
- 3.1 Introduction
- 3.2 创新点
- 4. 网络结构
- 4.1 数据分析
- 4.2 混合深度学习框架的发展
- 4.3 Mul
- 4.4 CNN block
- 4.5 GCN block
- 4.6 GRU block
- 4.7 注意力机制
- 4.8 模型评估标准
- 5. 实验结果
- 5.1 不同邻接矩阵的性能评价
- 5.2 不同预测模式的性能评价
- 5.3 不同预测方法的多步预测性能
- 6. 结论
- 参考文献
week 63 GCN-CNNGA
摘要
本周阅读了题为A hybrid deep learning framework for predicting industrial wastewater influent quality based on graph optimisation的论文。该文构建了GCN优化的CNN-GRU-Attention模型(GCN-CNNGA)。该框架通过集成图卷积网络(GCN)、卷积神经网络(CNN)、门控循环单元(GRU)和注意机制,有效捕获了输入数据的高维特征和变量间的复杂非线性时空模式。具体来说,CNN从时间序列中提取关键局部特征,GCN捕获关键影响参数之间的拓扑信息,GRU捕获长期依赖关系,而注意机制优化了权重分布。在华东某工业园区的实际数据测试中,GCN-CNNGA模型在预测精度和鲁棒性方面均优于主流方法。
Abstract
This week’s weekly newspaper decodes the paper entitled A hybrid deep learning framework for predicting industrial wastewater influent quality based on graph optimisation. This paper constructs the GCN-optimized CNN-GRU-Attention model (GCN-CNNGA). The framework effectively captures high-dimensional features of input data and complex nonlinear spatiotemporal patterns between variables by integrating Graph Convolutional Networks (GCN), Convolutional Neural Networks (CNN), Gated Recurrent Units (GRU), and attention mechanisms. Specifically, CNN extracts key local features from time series data, GCN captures topological information between key influencing parameters, GRU captures long-term dependencies, and the attention mechanism optimizes weight distribution. In practical data tests from an industrial park in East China, the GCN-CNNGA model outperforms mainstream methods in terms of prediction accuracy and robustness.
1. 题目
标题:A hybrid deep learning framework for predicting industrial wastewater influent quality based on graph optimisation
作者:Jiafei Cao a, Anke Xue a, Yong Yang a, Rongfeng Lu a, Xiaojing Hu a, Le Zhang a, Wei Cao b, Guanglong Cao b, Xiulin Geng c,*, Lin Wang d
发布:Journal of Water Process Engineering
- https://doi.org/10.1016/j.jwpe.2024.105831
- Volume 30, Number 1, February 2025
2. Abstract
由于进水水质过高和水量波动的影响,目前的工业污水处理厂无法保持稳定的去污能力,对生态环境构成严重威胁。因此,预测itp的进水质量以促进预测性维护是必要的。然而,由于工业废水的高度非线性和变异性,单一模型往往具有有限的预测精度。因此,本研究创新性地构建了一个全面、高适应性的混合深度学习预测框架——GCN优化CNN-GRU-attention model (GCN - cnnga)。该框架通过集成图卷积网络(GCN)、卷积神经网络(CNN)、门控循环单元(GRU)和注意机制,有效捕获了输入数据的高维特征和变量间复杂的非线性时空模式。具体来说,使用CNN从IETP时间序列中准确提取关键的局部特征。在此基础上,利用GCN进一步捕获关键影响参数之间的拓扑信息,揭示它们的相互联系,并深入挖掘污染物之间的复杂依赖关系。GRU有效地捕获了上述过程中未考虑的长期依赖关系,而注意机制优化了权重分布,从而提高了预测的精度。在华东某工业园区的实际数据测试中,GCN-CNNGA模型在预测精度和鲁棒性方面均优于主流预测方法。本研究建立的高精度预测模型有望显著提高ietp的预测维护水平,为维持最佳运行状态提供强有力的技术支持,对保护生态环境和促进可持续发展具有重要意义。
3. 文献解读
3.1 Introduction
Zhang等[27]建立了一种基于lstm的神经网络模型,用于污水处理厂进水COD、TN、TP的快速检测,其预测R2比传统机器学习算法高46.20 ~ 61.22%。近年来,研究试图使用基于深度学习的混合框架来开发废水流入的预测模型。
Zhou等人[29]引入了MLP和LSTM相结合的方法来预测实际污水处理厂每小时的进水特征,为高分辨率预测废水进水特征提供了有价值的支持。
Yan等[32]提出了一种基于GRU和VMD滚动分解的集成深度学习算法模型,用于预测污水处理厂进水铵。结果表明,与单一GRU相比,该模型将RMSE降低16.69%,MAE降低13.02%,MAPE降低11.90%。
作为一种先进的深度学习技术,GCNs适用于处理复杂网络结构中的数据,如工业废水系统中的多参数交互。通过学习污水参数之间的复杂关系和模式,GCN可以更准确地预测污染物的行为和趋势。
3.2 创新点
鉴于深度学习模型框架(如CNN、GRU、注意力机制和GCN)在特定场景下的优异性能,开发了一种混合深度学习预测框架(GCN - cnnga)来解决ietp中建模影响的挑战性问题。本研究的主要贡献如下:
- 考虑到变量之间复杂的非线性关系和相互耦合现象,从时空角度提出了一种混合深度学习预测框架。该算法可以实现对IETP进水参数的准确短期预测,显著提高了工业废水处理的效率和效果。
- 该算法首先使用CNN进行多层迭代,将模型集中在与预测目标最相关的特征上,并捕获进水参数的高维特征。然后构造一个特征邻接矩阵,反映参数变量之间复杂的相互作用。GCN对高维特征的相邻信息进行聚合和传递,有效挖掘高维特征之间的空间依赖关系。在此过程中,通过对相邻特征的加权聚合更新节点的特征表示,实现对局部拓扑结构和节点特征信息的综合学习,增强了模型对水质动态变化的预测能力。
- 为了捕捉进水参数随时间变化的动态特征,该算法框架集成了GRU模块,自适应提取不同时间尺度上的长期时间依赖关系。此外,采用注意机制加强不同特征信息的时变影响,从而有效提高了IETP进水参数的预测精度。
- 通过对IETP流量预测的实际案例研究,验证了该方法在实际应用中的有效性和准确性,为IETP的运行管理提供了稳健、稳定的技术支持。
4. 网络结构
4.1 数据分析
本研究使用的污水数据来自华东某工业园区的IETP。园区现有化工企业52家,主要生产环氧树脂、聚酯树脂、邻苯二甲酸酐等化工产品。IETP的日处理能力为5000t。本研究使用的数据包括进水流量、日进水量、累计进水量、进水COD (CODin)、进水NH3-N (NH3-Nin)、进水TP (TPin)、进水TN (TNin)。这些参数具有某些相互关联的属性,深入分析可以产生丰富的关键信息。
本研究采用KNN方法对原始数据中的缺失值进行估算。
在数据进入模型之前,应用线性归一化将所有特征缩放到[0,1]范围。该方法可以避免输入特征的幅度差异带来的干扰,防止神经网络中出现梯度爆炸或梯度消失等问题,从而提高模型的预测性能。
4.2 混合深度学习框架的发展
为了提供稳定准确的IETP流量预测模型,本研究提出了一种混合深度学习预测框架,即GCN-CNNGA。这种方法的概念框架如图2所示。输入到GCN-CNNGA的时间序列数据由7个入口参数组成,
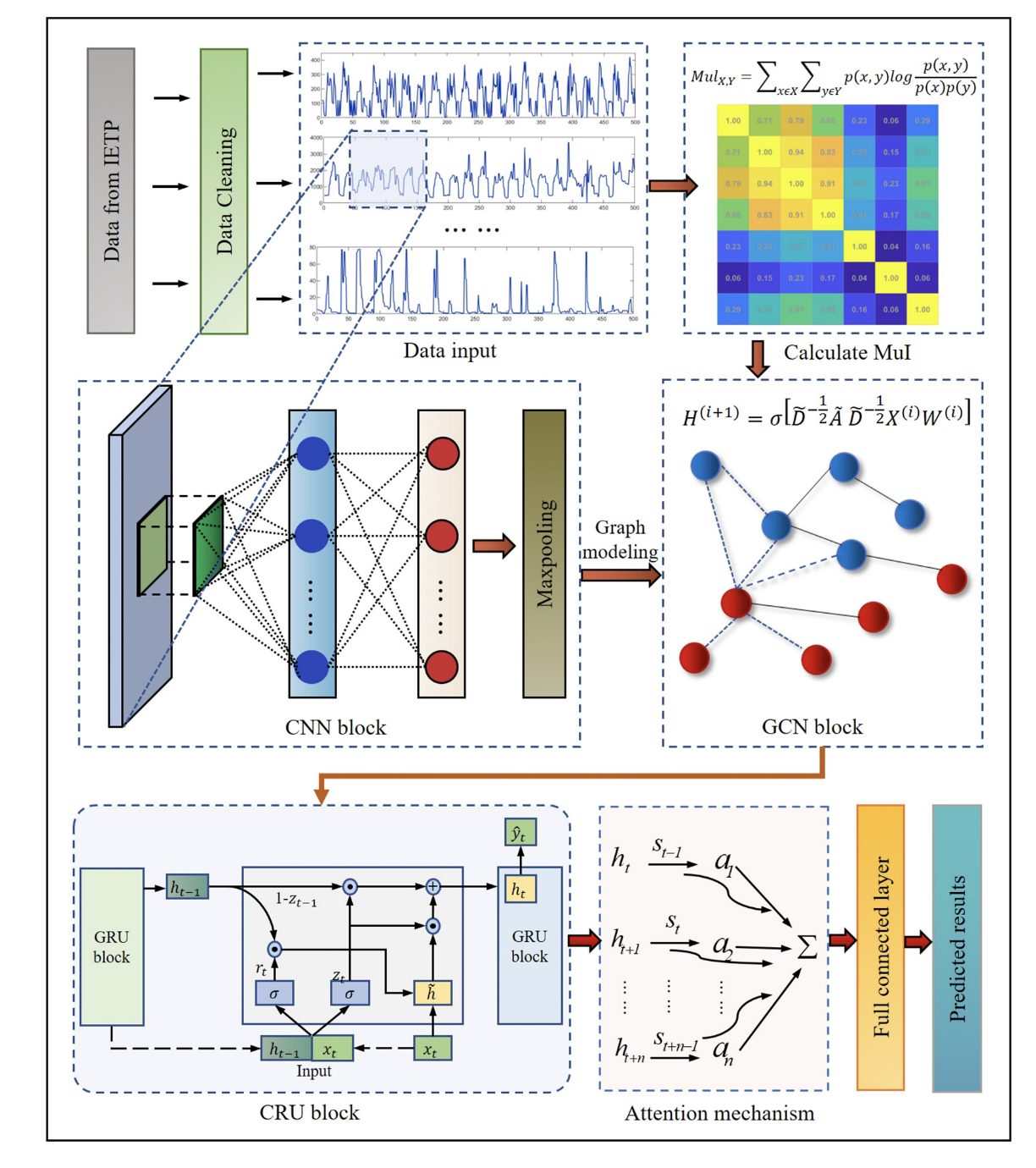
采用CNN、GCN、GRU和注意机制作为深度学习网络,并将这四种算法进一步耦合。模型的结构超参数包含一个包含32个神经元的CNN层,核大小为3,激活函数为ReLU。GCN层包含128个神经元,dropout率为0.01。该模型包含两个GRU层,每层分别有258和128个神经元。参与注意机制的神经元有256个。基于Adam优化器进行模型训练,损失函数设为平均绝对误差。epoch设置为150,batch大小设置为512。然后,按照以下步骤预测IETP的流量:
- 将获取的IETP进水数据 S = ( s 1 , s 2 , … , s n ) T S = (s_1, s_2,…,s_n)^T S=(s1,s2,…,sn)T划分为训练集、验证集和测试集。将训练集作为CNN模型的输入,从IETP时间序列中准确提取关键的局部特征。
- 将CNN模型中提取的特征输入到GCN模型中。利用GCN进一步捕获关键IETP流入参数之间的拓扑信息,聚合并传输高维特征的邻接信息。通过逐层信息融合,揭示关键影响参数之间的相互关系,深入挖掘污染物之间的复杂依赖关系。
- GRU模型使用GCN模型提取的特征作为输入,进一步捕获数据中的时间依赖关系。利用注意机制增强模型对关键信息的关注,从而提高预测性能。整体模型输出,反映最终预测的IETP流入数据 Y = ( y 1 , y 2 , … , y n ) T Y = (y_1, y_2,…,y_n)^T Y=(y1,y2,…,yn)T,是使用全连接层生成的。
为了评估所提出的GCN-CNNGA预测模型的性能,测试了两种传统的时间序列预测机器学习模型,即RF和SVM,以及三种深度学习模型,即ANN, LSTM和TCN。TCN和GCN的主要区别在于它们的数据类型和结构:TCN是为序列数据设计的,利用一维卷积层捕获时间依赖性,而GCN是为图结构数据定制的,利用图卷积层掌握序列之间的拓扑关系和特征信息。此外,消融研究分别使用GCN和CNNGA模型进行。为了实现每个模型的最佳预测精度,执行网格搜索以进行参数调优,表3列出了最佳参数。为了保持深度学习模型之间的一致性,设置学习率为0.001,并在所有模型的训练期间以7:2:1的比例将IETP进水特征序列划分为训练、验证和测试数据集。在一台配备2.6 GHz CPU和NVIDIA RTX4060ti GPU的计算机上,对所提出的GCN-CNNGA预测模型和其他比较方法进行了计算。使用Python编程,使用TensorFlow软件包。
4.3 Mul
MuI是一种用于度量两个随机变量之间相关性的非参数方法。在考察IETP中进水参数之间的关系时,MuI分析可以提供更全面的视角,捕捉线性和非线性关系以及双向相互作用[38]。对于IETP时间序列数据集,首先将每个时间序列划分为离散区间或使用直方图等方法进行离散。对离散时间序列数据集计算每对时间序列的MuI。对数据集中的每对时间序列计算MuI序列。MuI相关系数MuIX,Y在x(t)和Y (t)之间可以定义为:
M u l X , Y = ∑ x ∈ X ∑ y ∈ Y p ( x , y ) log p ( x , y ) p ( x ) p ( y ) (3) Mul_{X,Y}=\sum_{x\in X}\sum_{y\in Y}p(x,y)\log\frac{p(x,y)}{p(x)p(y)}\tag{3} MulX,Y=x∈X∑y∈Y∑p(x,y)logp(x)p(y)p(x,y)(3)
输入: I E T P 输入参数 x ( t ) , y ( t ) ,时滞 τ 输出:邻接矩阵 A 1 :定义 M u l ( v a r 1 , v a r 2 )计算特征的 M u I 2 : M u l X , Y = ∑ x ∈ X ∑ y ∈ Y p ( x , y ) log p ( x , y ) p ( x ) p ( y ) 3 :定义函数 s o f t m a x ( x ) 计算 s o f t m a x 函数,将输入向量变换为 s o f t m a x 。 4 :归一化向量 x ( t ) ,向量 y ( t ) 在 0 到 1 之间 5 : f o r t i n r a n g e ( t ) : 6 : X = a r r a y [ x ( t ) ] ; Y = a r r a y [ Y ( t ) ] 7 : M u I i n f o = M u l X , Y / / c a l c u l a t e o f M u I f e a t u r e s 8 : e n d 9 : m a t r i A ( M u I i n f o ) / / 向矩阵 A 添加 M u I 值 10 : e n d \begin{aligned} &输入:IETP输入参数x(t), y(t),时滞τ \\&输出:邻接矩阵A \\&1:定义Mul(var1, var2)计算特征的MuI \\&2: Mul_{X, Y} =\sum_{x\in X}\sum_{y\in Y}p(x, y)\log \frac{p(x, y)} {p(x)p(y)} \\&3:定义函数softmax(x)计算softmax函数,将输入向量变换为softmax。 \\&4:归一化向量x(t),向量y(t)在0到1之间 \\&5: for t in range(t): \\&6:X = array[x(t)]; Y = array[Y (t)] \\&7: MuI_info = Mul_{X,Y}//calculate\ of\ MuI\ features \\&8: end \\&9: matri_A(MuI_info)//向矩阵A添加MuI值 \\&10:end \end{aligned} 输入:IETP输入参数x(t),y(t),时滞τ输出:邻接矩阵A1:定义Mul(var1,var2)计算特征的MuI2:MulX,Y=x∈X∑y∈Y∑p(x,y)logp(x)p(y)p(x,y)3:定义函数softmax(x)计算softmax函数,将输入向量变换为softmax。4:归一化向量x(t),向量y(t)在0到1之间5:fortinrange(t):6:X=array[x(t)];Y=array[Y(t)]7:MuIinfo=MulX,Y//calculate of MuI features8:end9:matriA(MuIinfo)//向矩阵A添加MuI值10:end
4.4 CNN block
利用了CNN块的稀疏连接和权值共享,从而有效降低了复杂IETP数据特征提取的复杂性。CNN块使用卷积滤波器从数据中提取局部时间特征,并通过多次迭代将这些局部特征逐渐转化为全局、高维的抽象特征表示。
将输入数据描述为矩阵 X = ( x 1 , x 2 , … , x n ) T = ( x 1 , x 2 , … , x t ) ∈ R n × t X = (x_1, x_2,…,x_n)^T = (x_1, x_2,…,x_t)\in R^{ n×t} X=(x1,x2,…,xn)T=(x1,x2,…,xt)∈Rn×t,其中n为流入变量数,T为总时间长度。对于给定的卷积核K∈m,m < n,t,在时间步长j处的卷积运算输出可以表示为:
C i , j = ∑ a = 0 m − 1 K a ⋅ X i , j + a + b (4) C_{i,j}=\sum^{m-1}_{a=0}K_a\cdot X_{i,j+a}+b\tag{4} Ci,j=a=0∑m−1Ka⋅Xi,j+a+b(4)
4.5 GCN block
GCN使用堆叠图卷积层对每个节点进行局部邻域信息聚合。这是通过邻接矩阵加权的特征传输来实现的,它允许每层的输出递归地捕获高阶空间特征依赖
对于图G(V, E),定义如下:V是节点的集合,表示CNN输出的高维特征信息,E是边的集合,描述节点之间的邻接关系。对于每个节点i,有一个特征xi,由矩阵XN*D表示,其中Nis为节点数,D为节点i的特征数。为了简化实现,GCN主要通过映射到频域的卷积操作,基于特征邻接矩阵提取空间特征。图G(V, E)的特征信息可以用拉普拉斯矩阵L表示,如下式所示:
L = I N − D ~ − 1 2 A ~ D ~ − 1 2 (5) L=I_N-\tilde D^{-\frac12}\tilde A\tilde D^{-\frac12}\tag{5} L=IN−D~−21A~D~−21(5)
由矩阵的特征分解得到的特征值和特征向量可以用来研究图的信息。拉普拉斯矩阵L是一个允许分解的对称半正定矩阵。可以表示为:
L = U Λ U − 1 = U Λ U T (6) L=U\Lambda U^{-1}=U\Lambda U^T\tag{6} L=UΛU−1=UΛUT(6)
F ( λ 1 ) = f ^ ( λ 1 ) = ∑ i = 1 N f ( i ) u t ( i ) (7) F(\lambda_1)=\hat f(\lambda_1)=\sum^N_{i=1}f(i)u_t(i)\tag{7} F(λ1)=f^(λ1)=i=1∑Nf(i)ut(i)(7)
根据图的傅里叶变换,图的卷积公式如下:
g ∗ x = U g θ ( L ) U T x = U [ g ^ ( λ 1 ) g ^ ( λ 2 ) ⋱ g ^ ( λ N ) ] U T x g^*x=Ug_{\theta}(L)U^Tx=U \left[ \begin{aligned} &\hat g(\lambda_1)\\ &\quad\quad\quad \hat g(\lambda_2)\\ &\quad\quad\quad\quad\quad\quad \ddots \\ &\quad\quad\quad\quad\quad\quad\quad\quad\quad \hat g(\lambda_N) \\ \end{aligned} \right]U^Tx g∗x=Ugθ(L)UTx=U g^(λ1)g^(λ2)⋱g^(λN) UTx
使用切比雪夫多项式T(x)的K阶截断来近似卷积:
g θ = ∑ i = 1 N θ k T k ( L ~ ) (9) g_\theta=\sum^N_{i=1}\theta_kT_k(\tilde L)\tag{9} gθ=i=1∑NθkTk(L~)(9)
式中, L = 2 ( L − L N ) / λ m a x L = 2(L−L_N)/λ_{max} L=2(L−LN)/λmax是拉普拉斯矩阵L的最大特征值,θ∈λ K是切比雪夫多项式的系数向量。根据Chebyshev多项式的递归定义,得到:
T k ( x ) = 2 x T k − 1 ( x ) − T k − 2 ( x ) , T 0 ( x ) = 1 , T 1 ( x ) = x (10) T_k(x)=2xT_{k-1}(x)-T_{k-2}(x),T_0(x)=1,T_1(x)=x\tag{10} Tk(x)=2xTk−1(x)−Tk−2(x),T0(x)=1,T1(x)=x(10)
假设k = 1 λmax = 2等于引入ChebNet的一阶近似
g ∗ x = θ D ~ − 1 2 A ~ D ~ − 1 2 x (11) g^*x=\theta\tilde D^{-\frac12}\tilde A\tilde D^{-\frac12}x\tag{11} g∗x=θD~−21A~D~−21x(11)
因此,图卷积分层传播的最终简化公式可以表示为:
H i + 1 = σ [ D ~ − 1 2 A ~ D ~ 1 2 X ( i ) W ( i ) ] (12) H^{i+1}=\sigma [\tilde D^{-\frac12}\tilde A \tilde D^{\frac12}X^{(i)}W^{(i)}]\tag{12} Hi+1=σ[D~−21A~D~21X(i)W(i)](12)
式中,σ(⋅)表示激活函数,W(i)为可训练权矩阵,X(i)表示第i层的激活值,其中X(0) = X为初始输入。
利用GCN的优势,通过MuI构造的特征邻接矩阵揭示了IETP流入参数之间的相互依赖关系,有效地整合了图结构信息和节点特征。
4.6 GRU block
GRU模型来捕获不同时间尺度上IETP流入特征序列的长期时间依赖性。gru——lstm的优化变体——减少了训练参数的数量,确保了较高的预测精度[40]。与LSTM相比,GRU门结构更少,收敛速度更快,对数据特征的学习能力更强。这在一定程度上缓解了梯度消失或爆炸的问题;它还可以更有效地处理具有复杂时间依赖关系的IETP进水特征序列,并揭示它们在时间维度上的复杂关联。
GRU单元内的数据传播过程如下:首先,利用先前传输的求值状态ht−1和当前节点的输入xt获得复位门和更新门的状态。
τ t = σ ( x t W x r + h t − 1 W h r + b r ) (13) \tau_t=\sigma(x_tW_{xr}+h_{t-1}W_{hr}+b_r)\tag{13} τt=σ(xtWxr+ht−1Whr+br)(13)
z t = σ ( x t W x r + h z ) (14) z_t=\sigma(x_tW_{xr}+h_z)\tag{14} zt=σ(xtWxr+hz)(14)
接下来,将当前ω h集合中记忆的当前矩态表示为:
h ~ t = tanh ( x t W h r + R t ⊙ h t − 1 W h h + b h ) (15) \tilde h_t=\tanh(x_tW_{{hr}}+R_t\odot h_{t-1 W_{hh}+b_h})\tag{15} h~t=tanh(xtWhr+Rt⊙ht−1Whh+bh)(15)
随后,GRU模型使用以下公式更新状态
h t = ( 1 − Z t ) ⊙ h t − 1 + Z t ⊙ h ~ t (16) h_t=(1-Z_t)\odot h_{t-1}+Z_t\odot\tilde h_t\tag{16} ht=(1−Zt)⊙ht−1+Zt⊙h~t(16)
利用先前传输的状态ht−1和当前节点的输入xt,将数据转换为0-1范围内的值,从而作为门控信号。在这种情况下,ht−1包含过去的信息,rt表示复位门,⊙表示Hadamard积
最后,前向传播的输出由下式给出
y t = σ ( W o ⋅ h t ) (17) y_t=\sigma(W_o\cdot h_t)\tag{17} yt=σ(Wo⋅ht)(17)
4.7 注意力机制
注意机制将查询Q (Query)、键K (Key)和值V (Value)映射到输出,然后使用softmax层将其映射到范围。给定dk维的Q和K, dv维的V,点积注意力的计算过程如下:
A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) V (18) Attention(Q,K,V)=softmax(\frac{QK^T}{\sqrt {d_k}})V\tag{18} Attention(Q,K,V)=softmax(dkQKT)V(18)
4.8 模型评估标准
本研究采用MSE、RMSE、MAE和R2三个评价指标对实验模型进行评价。这些指标用于评估预测模型,并将其与基准实验模型进行比较。
5. 实验结果
5.1 不同邻接矩阵的性能评价
本文提出的方法引入相关性来描述IETP进水参数之间的关系,并使用实验导出的关系矩阵作为邻接矩阵来提高GCN-CNNGA模型的预测能力。一些研究通过各种相关分析建立了邻接矩阵。例如,Zhao等人开发了一个基于GCN的模型,通过使用SCC构建邻接矩阵来预测风力发电[44]。类似地,Lin等人使用带有GCN的PCC来模拟特征之间的关系[45]。研究了不同类型的相关系数(包括MuI、SCC和PCC)对邻接矩阵构造的影响。讨论的重点是这些相关度量在揭示变量之间的复杂关系及其对基于图的模型性能的后续影响方面的有效性。
PCC用于度量两个变量之间的线性相关性。对于每对IETP时间序列数据集,序列x(t)与序列Y (t)之间的相关系数PCCX,Y可定义为:
P C C X , Y = c o v ( X , Y ) σ X σ Y = E [ ( X − μ X ) ( Y − μ Y ) ] σ X σ Y (23) PCC_{X,Y}=\frac{cov(X,Y)}{\sigma_X\sigma_Y}=\frac{E[(X-\mu_X)(Y-\mu_Y)]}{\sigma_X\sigma_Y}\tag{23} PCCX,Y=σXσYcov(X,Y)=σXσYE[(X−μX)(Y−μY)](23)
SCC首先对每个时间序列进行排序,得到相应的秩。对于排序时间序列数据集,计算每对时间序列的SCC。SCC测量两个变量之间的单调相关性。序列x(t)与序列Y (t)之间的相关系数 S C C X , Y SCC_{X,Y} SCCX,Y定义如下:
S C C X , Y = 1 − 6 ∑ d i 2 n ( n 2 − 1 ) (24) SCC_{X,Y}=1-\frac{6\sum d^2_i}{n(n^2-1)}\tag{24} SCCX,Y=1−n(n2−1)6∑di2(24)
基于各相关系数法构建的邻接矩阵如图3所示。

使用MSE、RMSE和MAE指标对模型进行评估,如图4所示。
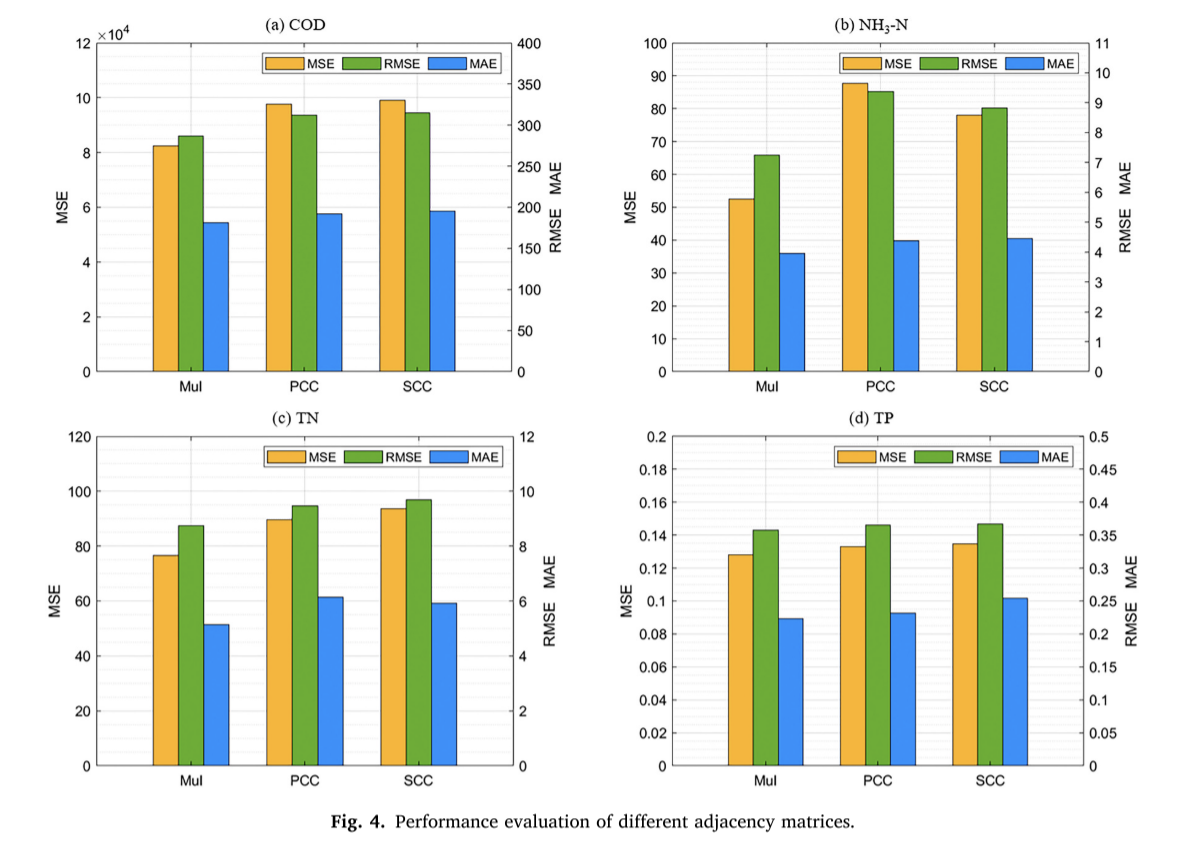
结果分析表明,使用MuI作为输入时,GCN-CNNGA模型的预测性能显著优于使用PCC和SCC作为输入时的预测性能。
5.2 不同预测模式的性能评价
所提出的混合深度模型与经典时间序列预测模型的对比实验结果如表4所示,其中展示了这些建模方法预测精度的统计数据,使用MAE、RMSE和R2进行测量。为了保证结果的稳定性和可靠性,所有模型的输入都采用相同的格式,每个实验显示的结果为五次训练的平均值。
从表4的对比结果来看,GCN-CNNGA模型在所有类型的进水水质预测中都具有最优的RMSE、MAE和R2值,在IETP数据集上的每个进水水质预测任务中都表现出优异的性能。
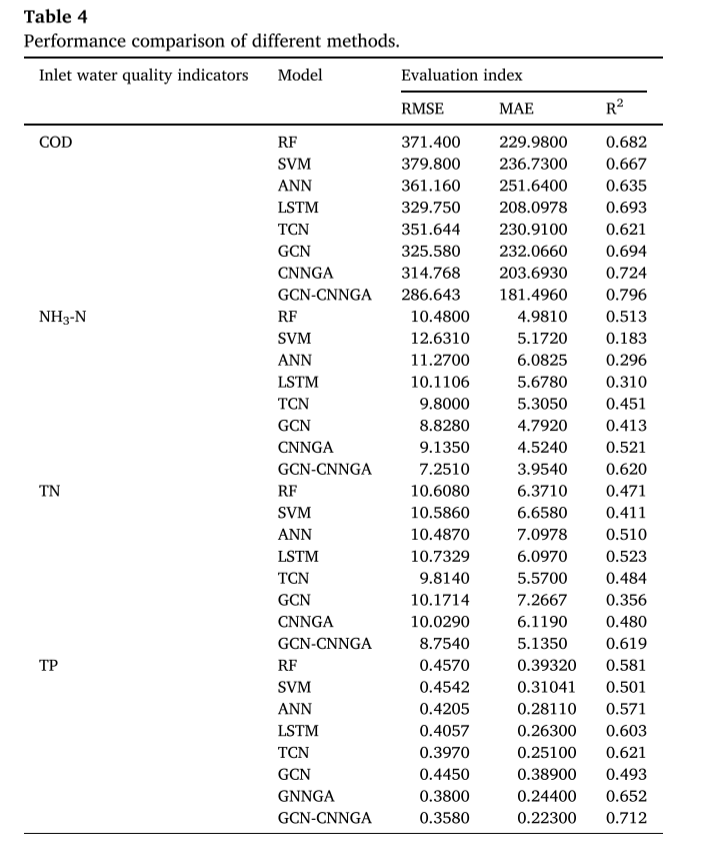
- GCN- cnnga模型将GCN作为其核心优化组件。GCN更深入地捕捉高维特征之间的非结构化空间依赖关系,增强特征之间的交互性和历史信息。相比之下,CNNGA模型主要依靠cnn来处理结构化数据,这在处理具有复杂相互关系的数据时可能存在局限性。
- GCN-CNNGA模型表现出更强的特征表示能力。该模型结合了GCN的全局信息处理能力和CNN的局部特征提取优势,从多个角度全面捕获数据特征。GCN通过聚合相邻信息更新节点表示,而CNN通过卷积层提取关键的局部特征。这种双重策略增强了GCN-CNNGA模型的数据表示,从而提高了预测精度。
- GCN-CNNGA模型的网络结构更加复杂,增加了额外的参数,不仅增强了模型对高度复杂数据的拟合能力,而且提高了模型的优化效果。与CNNGA模型相比,GCN-CNNGA模型可以对其参数进行精细调整,以适应不同的数据特征,从而显著提高了预测精度。
5.3 不同预测方法的多步预测性能
本节将GCN-CNNGA模型与其他适合长期预测的高级模型(LSTM和TCN-Transformer)进行比较。结果总结在表5中,表5显示了每个模型在1至8小时的时间间隔内预测四种入流水质指标的性能。
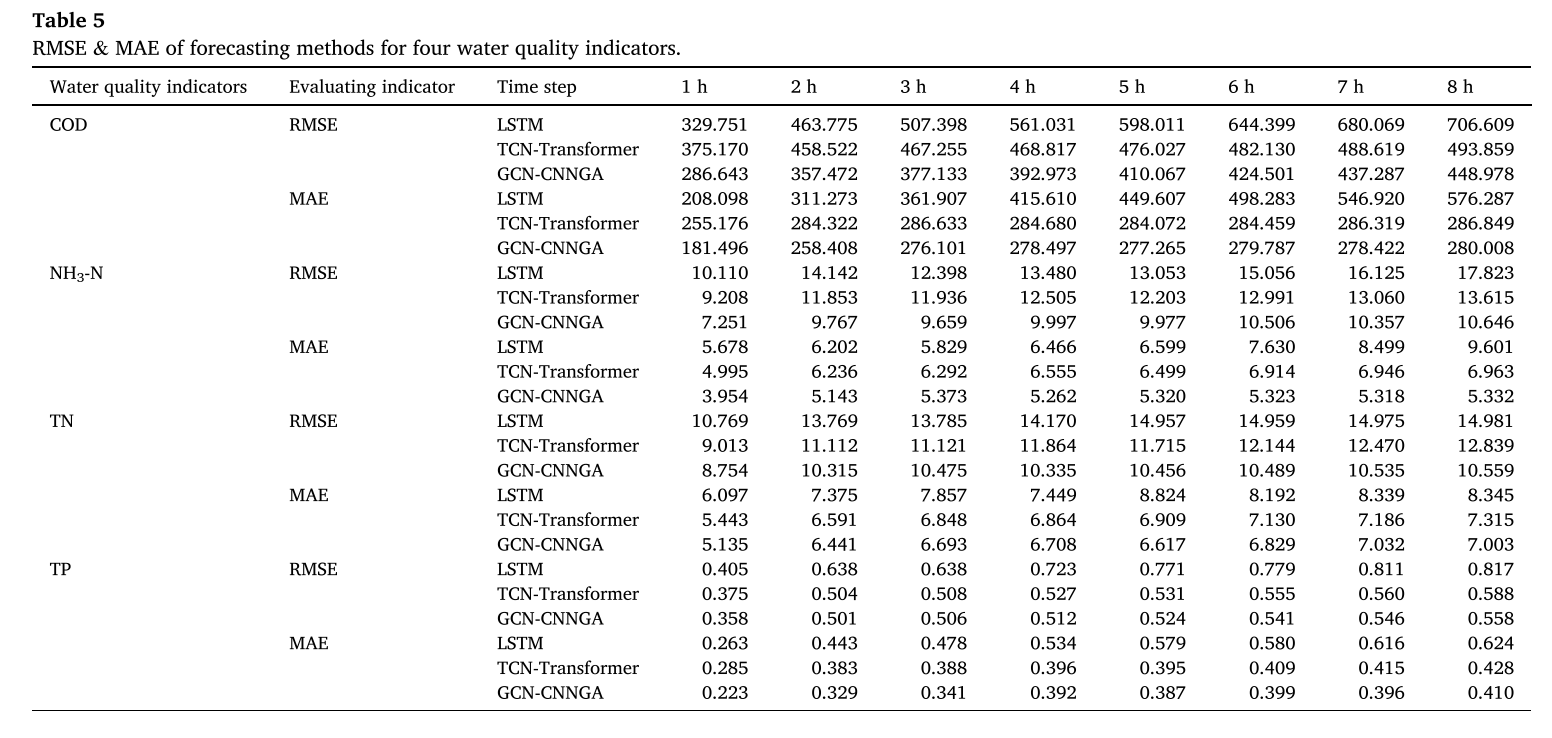
实验表明,随着预测时间范围的扩大,GCN-CNNGA模型有效地捕获了数据中固有的信息拓扑。它还强调了在长期预测任务中,随着时间的推移,更好地理解和利用数据相关性的复杂模式的重要性。GCN-CNNGA模型的稳定性和泛化能力在面对涉及更复杂的环境因素和非线性模式变量的预测任务时是有限的。
6. 结论
本研究创新性地应用GCN来优化CNNGA复合模型的深度学习框架,专门针对IETP进水参数预测的挑战,从而增强对IETP进水水质的模拟。通过华东某工业园区的实际应用验证,该模型有效地揭示了工业园区进水参数之间的非线性关系和复杂的拓扑结构。该预测模型通过将不同特征之间的拓扑信息作为GCN的邻域矩阵,能够更准确地捕捉高维特征之间的相似性和相关性。此外,CNN、GRU和注意力机制的应用进一步增强了模型捕捉数据时间依赖性的能力,在应对IETP进水水质参数剧烈变化的情况下表现出良好的性能。
参考文献
[1] Jiafei Cao a, Anke Xue a, Yong Yang a, Rongfeng Lu a, Xiaojing Hu a, Le Zhang a, Wei Cao b, Guanglong Cao b, Xiulin Geng c,*, Lin Wang d, A hybrid deep learning framework for predicting industrial wastewater influent quality based on graph optimisation, Journal of Water Process Engineering https://doi.org/10.1016/j.jwpe.2024.105831



















