0-1背包

什么是0-1背包问题？

[0-1背包问题Knapsack Problem] 假设有一个背包，可承载的最大重量是W(kg)， 现在有n个物品，每个物品的重量不等， 并且不可分割。我们期待选择几件物品放入背包中，在不超过背包最大承载重量的前提下，如何让背包中的物品总重量最大？

回溯法

分析

 int capacity = 4;int[] weight = {2, 1, 3};int[] val = {4, 2, 3};

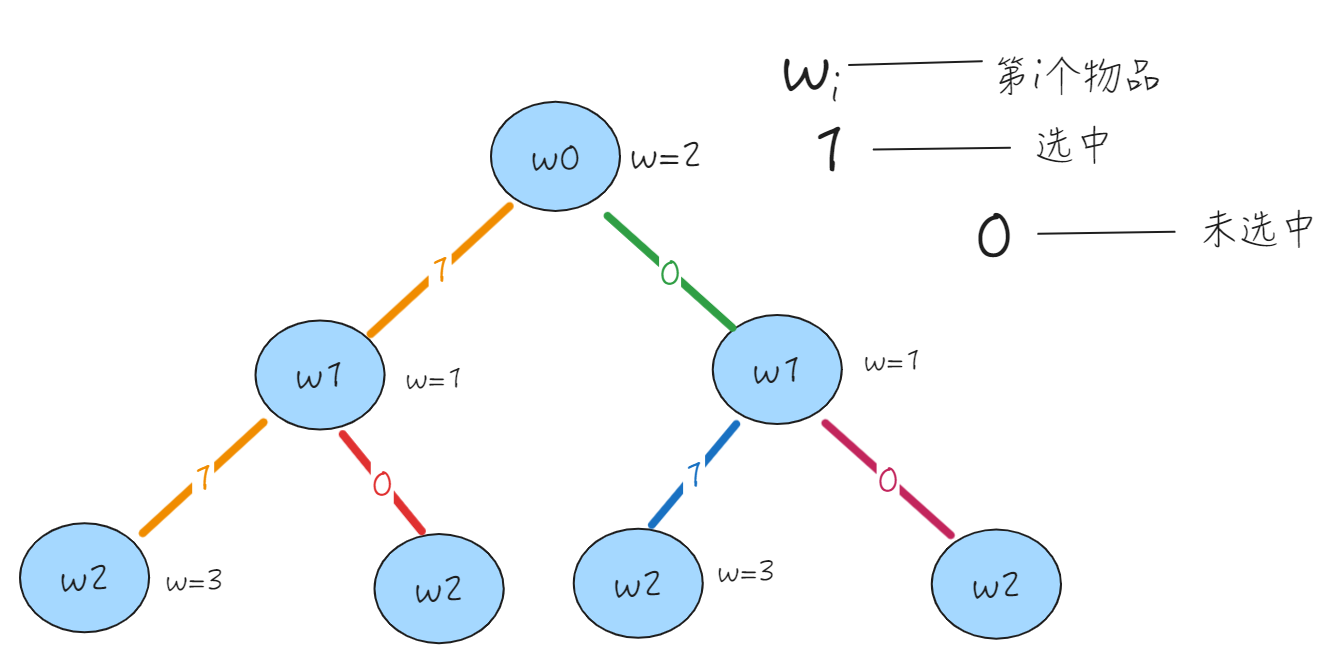
参考实现

import java.util.List;public class Knapsack {private final int[] weight;private final int[] val;private final int capacity; //背包容量（最大承载）private final int n; //物品数量private int perfectValue; //最大价值public Knapsack(int[] weight, int[] val, int capacity) {this.weight = weight;this.val = val;this.capacity = capacity;this.n = weight.length;}public int getPerfectValue() {return perfectValue;}public void dfs(int depth, int sumWeight, int sumVal) {if (depth == n) { //当前路径搜索完毕if (sumVal > perfectValue) {perfectValue = sumVal;}return;}if (sumWeight + weight[depth] <= capacity) {//总重+当前重量<=最大载重visited[depth] = true;dfs(depth + 1, sumWeight + weight[depth], sumVal + val[depth], visited);visited[depth] = false;}dfs(i + 1, sumWeight, sumVal);//不选择}public static void main(String[] args) {int[] weight = {2, 1, 3};int[] val = {4, 2, 3};int capacity = 4;Knapsack oOne = new Knapsack(weight, val, capacity);oOne.dfs(0, 0, 0);System.out.println(oOne.getPerfectValue());}
}

动态规划法

分析

在考虑第n个物品时，有两种状态需要考虑。

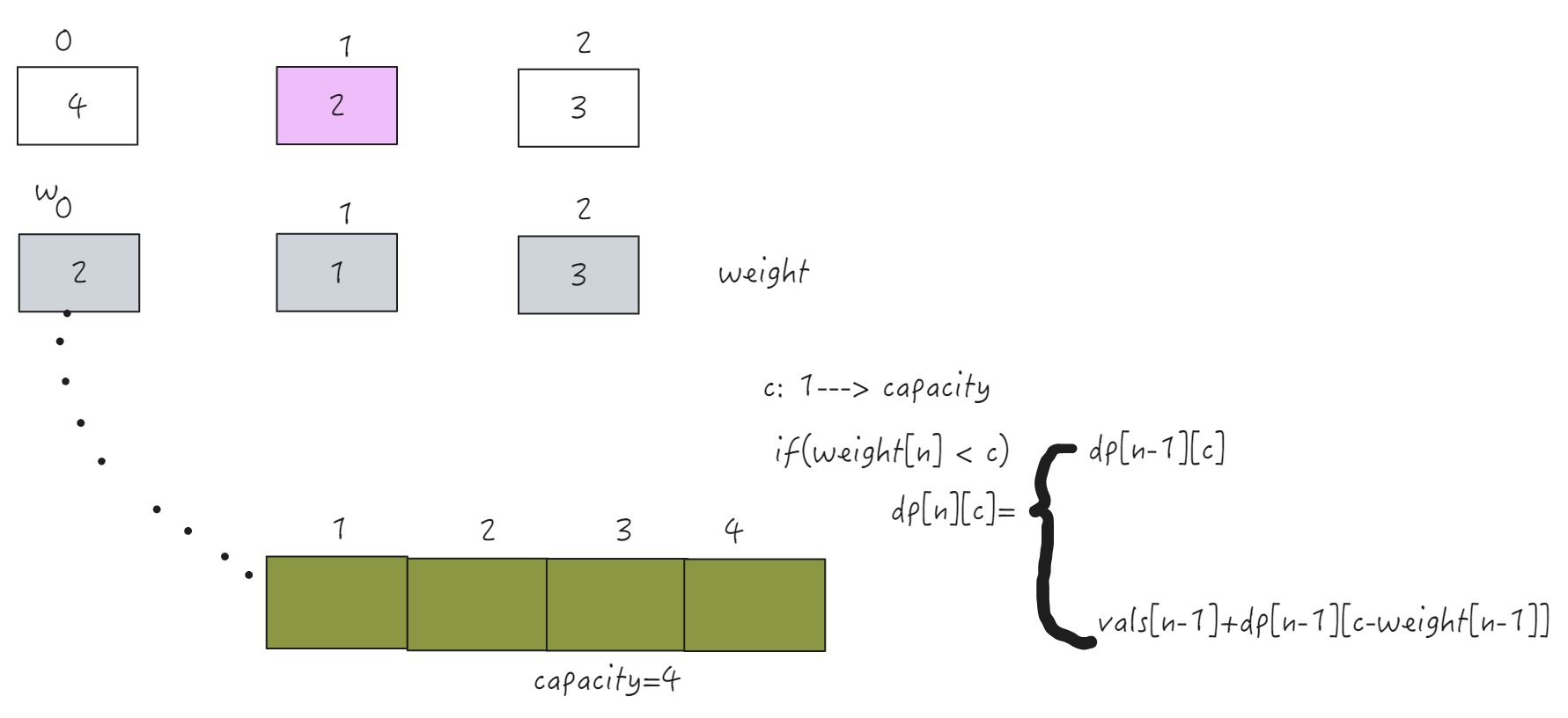
将第n个物品不放入背包

tips: 物品数量是从0开始， n个物品则为n-1

当前物品的最大价值 = 已经放入背包中物品的最大价值

dp[n-1][c]

将第n个物品放入背包

如果放入背包，那么当前物品的价格 = 之前物品的价值+ 剩余容量物品的价值。

dp[n-1][c-weight[n-1]]+vals[n-1])

参考实现

package com.ffyc.dp;public class KnapackDp {public int knapack(int[] weight, int[] vals, int capacity) {final int W = weight.length;int[][] dp = new int[W+1][capacity+1];for(int n = 1; n <= W;n++){for(int c = 1; c <= capacity;c++){if(weight[n-1] < c){dp[n][c]= Math.max(dp[n-1][c],dp[n-1][c-weight[n-1]]+vals[n-1]);}}}return dp[W][capacity];}public static void main(String[] args) {int[] weight = {2, 1, 3};int[] val = {4, 2, 3};int capacity = 4;System.out.println(new KnapackDp().knapack(weight, val, 4));}
}