前两天没有更新,这次把之前的补上,大篇章。
直接冲!!!
题目:找树坐下角的值
513. 找树左下角的值 - 力扣(LeetCode)
给定一个二叉树的 根节点 root,请找出该二叉树的 最底层 最左边 节点的值。
假设二叉树中至少有一个节点。
示例 1:
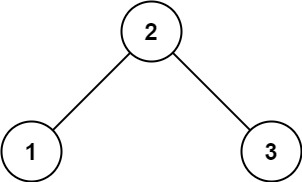
输入: root = [2,1,3] 输出: 1
题目分析:
方法一:层序遍历。层序是对树的每一层都去遍历,那么每一层的开始其实就是左下角的值。
方法二:递归遍历。这里的左下角在递归法中应该是深度最大的的叶子节点,而不是树中最左边的节点。所以根据这个深度我们就能找到这个节点。
//方法一:层序遍历
public class Solution {public int FindBottomLeftValue(TreeNode root) {Queue<TreeNode> temp=new Queue<TreeNode>();if(root!=null){temp.Enqueue(root);}int res=root.val;while(temp.Count>0){int size=temp.Count;for(int i=0;i<size;i++){TreeNode t=temp.Dequeue();if(i==0){res=t.val;}if(t.left!=null){temp.Enqueue(t.left);}if(t.right!=null){temp.Enqueue(t.right);}}}return res;}
}//方法二:递归法
public class Solution {int maxDepth=-1;int res=0;public int FindBottomLeftValue(TreeNode root) {BackTracking(root,0);return res;}public void BackTracking(TreeNode root,int depth){if(root.left==null&&root.right==null){if(depth>maxDepth){maxDepth=depth;res=root.val;}}if(root.left!=null){BackTracking(root.left,depth+1);}if(root.right!=null){BackTracking(root.right,depth+1);}return;}
}题目:路径总和
112. 路径总和 - 力扣(LeetCode)
给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径,这条路径上所有节点值相加等于目标和 targetSum 。如果存在,返回 true ;否则,返回 false 。
叶子节点 是指没有子节点的节点
题目分析:
寻找合适的路径,对树进行遍历,每次记录路径即可,加入回溯就能够遍历完所有路径了。题目要求返回一个布尔值,在遍历路径的时候将是否满足也返回出来判断是否提前结束遍历。
public class Solution {public bool HasPathSum(TreeNode root, int targetSum) {if(root==null) return false;return BackTracking(root,targetSum-root.val);}public bool BackTracking(TreeNode root,int target){if(root.left==null&&root.right==null&&target==0) return true; //满足条件if(root.left==null&&root.right==null&&target!=0) return false;if(root.left!=null){target-=root.left.val;if(BackTracking(root.left,target)) return true;//提前返回target+=root.left.val;}if(root.right!=null){target-=root.right.val;if(BackTracking(root.right,target)) return true;//提前返回target+=root.right.val;}return false;}
}题目:从中序和后序遍历中构造二叉树
106. 从中序与后序遍历序列构造二叉树 - 力扣(LeetCode)
给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。
题目分析:
中序遍历是左中右,后序遍历是左右中。就可以发现后序遍历数组中的最后一个值就是根节点,那么通过这个节点就可以在中序遍历中将根节点的左右子树分出来,然后继续通过后序遍历数组将左右子树继续划分。

看看代码:
public class Solution {public TreeNode BuildTree(int[] inorder, int[] postorder) {if(postorder.Length==0) return null;int m=postorder[postorder.Length-1];TreeNode root=new TreeNode(m);//根节点if(postorder.Length==1) return root;int index;for(index=0;index<inorder.Length;index++){//获取根节点在中序数组中的位置if(inorder[index]==m) break;}int[] in_Left=inorder.Take(index).ToArray();//划分数组int[] po_left=postorder.Take(index).ToArray();int[] in_right=inorder.Skip(index+1).ToArray();int[] po_right=postorder.Skip(index).Take(inorder.Length - index - 1).ToArray();root.left=BuildTree(in_Left,po_left);//递归继续划分root.right=BuildTree(in_right,po_right);return root;}
}对于数组的划分,其实有好几种方式。比如代码中的Take()截取到哪里结束。Skip(),从哪里开始截取。还有..的方式。
除了通过中序以及后序来构建外,还有通过前序和中序构造二叉树。本质上和这一题是一样的。需要注意对数组的区间划分位置。
105. 从前序与中序遍历序列构造二叉树 - 力扣(LeetCode)
public class Solution {public TreeNode BuildTree(int[] preorder, int[] inorder) {if(preorder.Length==0) return null;int m=preorder[0];TreeNode root=new TreeNode(m);if(preorder.Length==1) return root;int index;for(index=0;index<inorder.Length;index++){if(inorder[index]==m) break;}int[] p_left=preorder.Skip(1).Take(index).ToArray();int[] p_right=preorder.Skip(index+1).ToArray();int[] i_left=inorder.Take(index).ToArray();int[] i_right=inorder.Skip(index+1).ToArray();root.left=BuildTree(p_left,i_left);root.right=BuildTree(p_right,i_right);return root;}
}题目:最大二叉树
654. 最大二叉树 - 力扣(LeetCode)
给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:
- 创建一个根节点,其值为
nums中的最大值。 - 递归地在最大值 左边 的 子数组前缀上 构建左子树。
- 递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
示例 1:
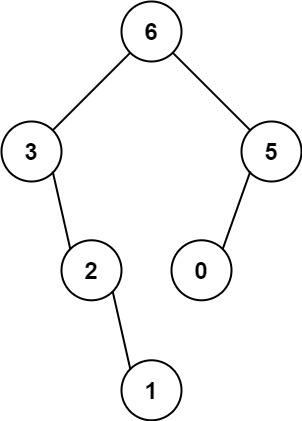
输入:nums = [3,2,1,6,0,5] 输出:[6,3,5,null,2,0,null,null,1] 解释:递归调用如下所示: - [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。- 空数组,无子节点。- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。- 空数组,无子节点。- 只有一个元素,所以子节点是一个值为 1 的节点。- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。- 只有一个元素,所以子节点是一个值为 0 的节点。- 空数组,无子节点。
题目分析:
其实这一题和上一题很像,无非是只有一个数组。根据题目的意思每次选取数组中的最大值作为根节点,然后划分数组,左子数组是左子树,右边就是右子树。然后同样的方式继续划分数组。
public class Solution {public TreeNode ConstructMaximumBinaryTree(int[] nums) {if(nums.Length==0) return null;int index=Max(nums);//选取最大值索引TreeNode root=new TreeNode(nums[index]);if(nums.Length==1) return root;//数组长度为一,叶子节点int[] left=nums.Take(index).ToArray();//划分int[] right=nums.Skip(index+1).ToArray();root.left=ConstructMaximumBinaryTree(left);//递归root.right=ConstructMaximumBinaryTree(right);return root;}public int Max(int[] nums){int res=0;for(int i=0;i<nums.Length;i++){if(nums[res]<nums[i]) res=i;}return res;}
}题目:合并二叉树
617. 合并二叉树 - 力扣(LeetCode)
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
注意: 合并过程必须从两个树的根节点开始。
题目分析:
合并两个二叉树,那么将A的节点加载B上就好了。每次递归的时候将两个树的结点同时传入其中。
public class Solution {public TreeNode MergeTrees(TreeNode root1, TreeNode root2) {if(root1==null) return root2;if(root2==null) return root1;root1.val+=root2.val;root1.left=MergeTrees(root1.left,root2.left);root1.right=MergeTrees(root1.right,root2.right);return root1;}
}题目:二叉搜索树中的搜索
700. 二叉搜索树中的搜索 - 力扣(LeetCode)
给定二叉搜索树(BST)的根节点 root 和一个整数值 val。
你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 null 。
题目分析:
二叉搜索树还记得吗?二叉搜索树的结点值满足左<中<右。根据这个特性,每次递归之前判断当前的结点值和目标值的大小,在去选择递归左边还是右边。
public class Solution {public TreeNode SearchBST(TreeNode root, int val) {if (root == null || root.val == val) return root;if (root.val > val) return SearchBST(root.left, val);if (root.val < val) return SearchBST(root.right, val);return null;}
}题目:验证二叉搜索树
98. 验证二叉搜索树 - 力扣(LeetCode)
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
- 节点的左
子树
只包含 小于 当前节点的数。 - 节点的右子树只包含 大于 当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
题目分析:
二叉搜索树的大小是左<中<右,这个顺序像什么呢?没错,树的中序遍历。这意味着二叉搜索树的中序遍历是一个递增的数组。所有验证搜索树就是验证中序数组的递增就好了。
public class Solution {long val=Int64.MinValue;public bool IsValidBST(TreeNode root) {if(root==null) return true;bool left=IsValidBST(root.left);if(root.val>val) val=root.val;else return false;bool right=IsValidBST(root.right);return left&&right;}
}题目:二叉搜索树的最小绝对差值
530. 二叉搜索树的最小绝对差 - 力扣(LeetCode)
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。
题目分析:
同样是二叉搜索树,那我们就需要考虑利用中序遍历的特殊性了。题目求得是最小差值,因为中序遍历是递增的,那么这个最小差值一定是相邻的两个位置。
public class Solution {List<int> arr=new List<int>();public int GetMinimumDifference(TreeNode root) {if(root==null) return 0;GetArray(root);if(arr.Count<2) return 0;int res=arr[arr.Count-1];for(int i=1;i<arr.Count;i++){res=Math.Min(res,arr[i]-arr[i-1]);}return res;}//对于二叉搜索树而言,中序遍历是一个有序数组public void GetArray(TreeNode root){//获取中序遍历if(root==null) return;GetArray(root.left);arr.Add(root.val);GetArray(root.right);}
}题目:二叉搜索树中的众数
501. 二叉搜索树中的众数 - 力扣(LeetCode)
给你一个含重复值的二叉搜索树(BST)的根节点 root ,找出并返回 BST 中的所有 众数(即,出现频率最高的元素)。
如果树中有不止一个众数,可以按 任意顺序 返回。
假定 BST 满足如下定义:
- 结点左子树中所含节点的值 小于等于 当前节点的值
- 结点右子树中所含节点的值 大于等于 当前节点的值
- 左子树和右子树都是二叉搜索树
题目分析:
又是一个二叉搜索树。求众数,就是出现最多的元素。考虑遍历的特性,因为数组是递增的,那么这个众数的出现一定是连续的。所以遍历之后统计出现的次数再排序是不是就找出来众数。不过这种写法比较麻烦。
那我们能不能再遍历的时候就把出现次数的统计以及众数的选择一起做了呢?
当然没问题,起初的中序遍历,中结点的处理只是收集结点而已,那么再处理结点的时候我们去比较这个结点和上一个结点的值是否相等,如果相等,计数加一,如果不等,计数和当前众数的大小比较,确实是否替换众数。
public class Solution {List<int> arr=new List<int>();int prev;//前一个结点的值int maxNum;//众数int num;//出现频率public int[] FindMode(TreeNode root) {prev=int.MinValue;maxNum=0;num=0;GetArray(root);return arr.ToArray();}public void GetArray(TreeNode root){if(root==null) return;GetArray(root.left);//处理结点if(root.val==prev){num++;}else{prev=root.val;//重新统计num=1;}if(num==maxNum){arr.Add(root.val);}else if(num>maxNum){//更新众数maxNum=num;arr.Clear();arr.Add(root.val);}GetArray(root.right);}题目:二叉树的最近公共祖先
236. 二叉树的最近公共祖先 - 力扣(LeetCode)
给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个节点 p、q,最近公共祖先表示为一个节点 x,满足 x 是 p、q 的祖先且 x 的深度尽可能大(一个节点也可以是它自己的祖先)。”
示例 1:
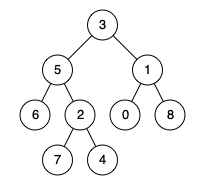
输入:root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1 输出:3 解释:节点5和节点1的最近公共祖先是节点3 。
题目分析:
寻找公共祖先,那我们自底向上查找不就好了吗?那怎么自底向上查找呢,当然是回溯啦,将查找结果返回给上一层。如果两个结果都不为空,那么上层就是他们的最近公共祖先了,不过需要注意的是,一个结点也可以是他自己的祖先。
public class Solution {public TreeNode LowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {if(root==p||root==q||root==null) return root;//找到结点或者遍历到了叶子节点TreeNode left=LowestCommonAncestor(root.left,p,q);//遍历左子树得到节点TreeNode right=LowestCommonAncestor(root.right,p,q);if(left!=null&&right!=null) return root;else if(left==null&&right!=null) return right;else if(left!=null&&right==null) return left;else{return null;}}
}
对于更详细的解析与其他语言的代码块,可以去代码随想录上查看。
代码随想录 (programmercarl.com)



















