杂记-LeetCode中部分题思路详解与笔记-HOT100篇-其三

时光荏苒啊，没想到这么快就到了四月份...

这个坑好久没写了，现在我们重启一下。

我看了一下之前的笔记，似乎是停留在了链表部分且HOT100中可以说最重要的链表题之一：LRU缓存居然没有写，真是岂有此理，让我们从这道脍炙人口的好题说起（好在哪呢）。

乍一看非常的唬人，如果你仔细阅读，会发现其实本质上get和put干的事就是哈希表干的事：查找和插入，当然他规定你必须以O1的时间复杂度进行，查找的时间复杂度为O1，那更离不开哈希表了，插入的时间复杂度也要为O1，那没办法了，只能上链表了。综上，显然这个题就是一个要用哈希表实现找，用链表实现插入的结构题。如果只是这样的话，那么不会非常困难，但其实LRU本身还有一个要求：最近最少使用，也就是一种算法思想：我们用的最少的东西就丢后面去，而一旦我们的容量达到上限，我们会优先摒弃最长时间未使用的数据，要在哈希表和链表的基础上实现这个功能才是关键。这里最难的部分其实是想到用双向链表来标记最长时间未使用的数据，这样我们可以直接把虚拟头结点的上一位丢掉，没有更繁琐的步骤。

我们首先写好链表部分的代码：

class Node{
public:int key,value;Node* prev,*next;Node(int k=0,int v=0):key(k),value(v){};
};

创建链表类，这里我们在构造函数里添加了一个默认参数值，这样即使我们用new Node()的写法也会自动给我们的key和value赋予0的值。当然，很重要的，别忘了Public。

private:Node* dummy;int capacity;unordered_map<int,Node*> mp;void remove(Node* node){node->prev->next=node->next;node->next->prev=node->prev;}void push_front(Node* node){node->prev=dummy;node->next=dummy->next;node->next->prev=node;node->prev->next=node;}Node* get_node(int x){auto it=mp.find(x);if(it==mp.end())return nullptr;Node* node=it->second;remove(node);push_front(node);return node;}

我们接着写了三个函数，移除，置前和查找。具体的函数内容都非常的简单而具体，不如说为什么要这样做呢？因为事实上当我们的Put函数调用时，我们要把这个put的节点放置到我们的链表的首部（因为他刚刚被使用过），我们当然也可以把这些所有功能全部塞进我们的put函数里，但那样会非常的不美观且看起来非常混乱。

public:LRUCache(int capacity):dummy(new Node()),capacity(capacity) {dummy->next=dummy;dummy->prev=dummy;}int get(int key) {auto node=get_node(key);return node==nullptr?-1:node->value;}void put(int key, int value) {auto node=get_node(key);if(node!=nullptr){node->value=value;return;}Node* toAdd=new Node(key,value);mp[key]=toAdd;push_front(toAdd);if(mp.size()>capacity){Node* toDelete=dummy->prev;mp.erase(toDelete->key);remove(toDelete);delete toDelete;}return;

剩下的就不用多说了，就是缺啥补啥。

class Node{
public:int key,value;Node* prev,*next;Node(int k=0,int v=0):key(k),value(v){};
};
class LRUCache {
private:Node* dummy;int capacity;unordered_map<int,Node*> mp;void remove(Node* node){node->next->prev=node->prev;node->prev->next=node->next;}void push_front(Node* node){node->prev=dummy;node->next=dummy->next;node->next->prev=node;node->prev->next=node;}Node* get_node(int x){auto it=mp.find(x);if(it==mp.end())return nullptr;Node* node=it->second;remove(node);push_front(node);return node;}
public:LRUCache(int capacity):dummy(new Node()),capacity(capacity) {dummy->next=dummy;dummy->prev=dummy;}int get(int key) {auto node=get_node(key);return node==nullptr?-1:node->value;}void put(int key, int value) {auto node=get_node(key);if(node!=nullptr){node->value=value;return;}Node* toAdd=new Node(key,value);mp[key]=toAdd;push_front(toAdd);if(mp.size()>capacity){Node* toDelete=dummy->prev;mp.erase(toDelete->key);remove(toDelete);delete toDelete;}return;}
};/*** Your LRUCache object will be instantiated and called as such:* LRUCache* obj = new LRUCache(capacity);* int param_1 = obj->get(key);* obj->put(key,value);*/

这个题只能说确实很麻烦，可以说是纯粹的模拟题：

我们要将二叉树退化成链表且要求链表的顺序符合先序链表，我们从根节点出发遍历所有节点，往左检查，如果当前根节点的左节点的值大于当前节点，我们就得丢到右边去，那么我们首先从左节点开始，往右边遍历到最后一个节点，然后把根节点的整个右子树接到左节点的最后一个右节点，然后再把整个左节点搬到右节点去：这么复杂的操作，无非是保留右子树的结构的同时把左节点换到右边，然后我们继续遍历左边的节点即可。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:void flatten(TreeNode* root) {TreeNode* cur=root;while(cur){if(cur->left){TreeNode* pre=cur->left,* tail=pre;while(tail->right)tail=tail->right;tail->right=cur->right;cur->left=nullptr;cur->right=pre;}cur=cur->right;}}
};

这个题要我们去求节点值之和为targetSum的路径数量，显然这里我们需要去遍历整个树并带着节点值了，最简单的做法自然就是将我们的targetSum作为函数参数的一部分，通过递归不断更新路径总量值来做，然后这里还需要注意的是我们没有要求一定经过根节点，那么除了根节点的部分我们还要考虑左右子树。

/*** Definition for a binary tree node.* struct TreeNode {*     int val;*     TreeNode *left;*     TreeNode *right;*     TreeNode() : val(0), left(nullptr), right(nullptr) {}*     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}*     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/
class Solution {
public:long long rootSum(TreeNode* cur, long long targetSum){if(!cur)return 0;long long res=0;if(cur->val==targetSum)++res;res+=rootSum(cur->left, targetSum-cur->val);res+=rootSum(cur->right, targetSum-cur->val);return res;}long long pathSum(TreeNode* root, long long targetSum) {if(!root)return 0;long long res=0;res+=rootSum(root, targetSum);res+=pathSum(root->left, targetSum);res+=pathSum(root->right, targetSum);return res;}
};

代码里的long long是因为有一些奇怪的样例无法用int通过，无伤大雅。

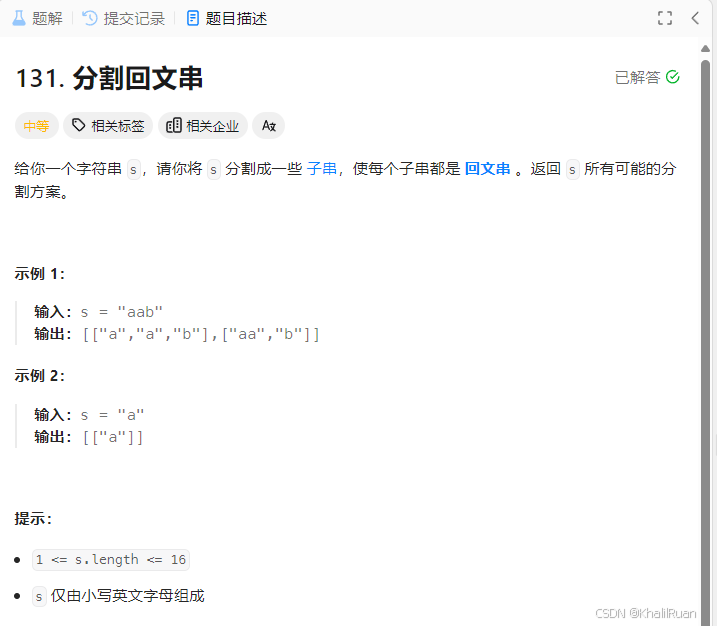
我们来看看回溯的题单，说实话，回溯这方面代码随想录的题单更优秀，总结得非常到位，推荐大家去做。回到题目本身，我们本质上要去不断划分子串并判断该子串是否为回文字串，那么不可避免地要写一个判断回文子串的辅助函数，至于如何划分这个子串的部分，不难发现其实就是回溯的过程：我们要不断地暴搜所有可能的划分情况并一个一个进行检查。

class Solution {
public:vector<vector<string>> res;vector<string> temp;bool helper(string s,int l,int r){while(l<r){if(s[l]!=s[r])return false;++l;--r;}return true;}void backtrack(string s,int index){if(index==s.size()){res.push_back(temp);return;}for(int i=index;i<=s.size();++i){if(helper(s,index,i)){temp.push_back(s.substr(index,i-index+1));backtrack(s,i+1);temp.pop_back();}}}vector<vector<string>> partition(string s) {backtrack(s,0);return res;}
};

这个题要求我们去找目标值的第一个和最后一个位置，其实就是找左边界和右边界嘛，那么如何找到左边界呢？我们依然用二分法，不过我们的判断条件发生一些改变：对于左边界来说，我们当然要用右指针来找：找到最后符合要求的右指针，就是我们的左边界；反之，我们最后符合要求的左指针就是我们的右边界。最后我们还要注意两点：第一是我们求出来的并不是最后符合的指针位置而是多向前了一位，或者说叫第一个不符合要求的下标，所以我们要进行一个基本的改动(l+1,r-1)；第二就是我们的l和r两个指针的间隔。

class Solution {
public:vector<int> searchRange(vector<int>& nums, int target) {int l=getLeft(nums,target),r=getRight(nums,target);if(l==-2)return {-1,-1};if(r-l>1)return {l+1,r-1};return {-1,-1};}int getLeft(vector<int>& nums, int target){int l=0,r=nums.size()-1,leftBound=-2;while(l<=r){int mid=(l+r)/2;if(target>nums[mid])l=mid+1;else{r=mid-1;leftBound=r;}}return leftBound;}int getRight(vector<int>& nums, int target){int l=0,r=nums.size()-1,rightBound=-2;while(l<=r){int mid=(l+r)/2;if(target<nums[mid])r=mid-1;else{l=mid+1;rightBound=l;}}return rightBound;}
};

旋转排序数组问题，最核心的思想就是去判断当前下标是在左边区间还是右边区间，除此之外也没有太多新东西。

对于寻找最小值，我们可以这样想：旋转后的数组就是两个递增区间组成的数组，那么我们就直接拿mid值和我们的nums.back()比较，因为最小值在第二个递增区间的第一个元素。

class Solution {
public:int findMin(vector<int>& nums) {int left=0,right=nums.size()-1;while(left<right){int mid=(left+right)/2;if(nums[mid]<nums.back()){right=mid;}else{left=mid+1;}}return nums[right];}
};

这个题就是标准的栈题，我们需要合理地规划整个流程并借助栈来模拟：

class Solution {
public:string decodeString(string s) {stack<pair<int,int>> stk;int count=0;string res;for(int i=0;i<s.size();++i){if(isdigit(s[i]))count=count*10+s[i]-'0';else if(s[i]=='['){stk.push({count,res.size()});count=0;}else if(isalpha(s[i])){res+=s[i];}else if(s[i]==']'){string temp=res.substr(stk.top().second,res.size()-stk.top().second);for(int i=0;i<stk.top().first-1;++i){res+=temp;}stk.pop();}}return res;}
};

这个题就是一个非常经典的最大堆模板题，不适用优先队列的前提下，我们去手搓一个堆来完成。

class Solution {
public:void maxHeapify(vector<int>& nums,int i,int heapSize){int l=2*i+1,r=2*i+2,largest=i;if(l<heapSize&&nums[largest]<nums[l])largest=l;if(r<heapSize&&nums[largest]<nums[r])largest=r;if(i!=largest){swap(nums[i], nums[largest]);maxHeapify(nums, largest, heapSize);}}void buildMaxHeap(vector<int>& nums,int heapSize){for(int i=heapSize/2;i>=0;--i){maxHeapify(nums, i, heapSize);}}int findKthLargest(vector<int>& nums, int k) {int n=nums.size();buildMaxHeap(nums, n);for(int i=nums.size()-1;i>=nums.size()-k+1;--i){swap(nums[i], nums[0]);--n;maxHeapify(nums, 0, n);}return nums[0];}
};

这是一个动态规划的题，不过比较阴险的是这是一个排列题（顺序不同对结果有影响），所以我们在遍历顺序上需要注意。

class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {int n=s.size();vector<bool> dp(n+1,false);dp[0]=true;unordered_set<string> set(wordDict.begin(),wordDict.end());for(int i=0;i<=n;++i){for(int j=0;j<i;++j){if(dp[j]&&set.contains(s.substr(j,i-j))){dp[i]=true;break;}}}return dp[n];}
};