LeetCode Hot100 - 普通数组篇

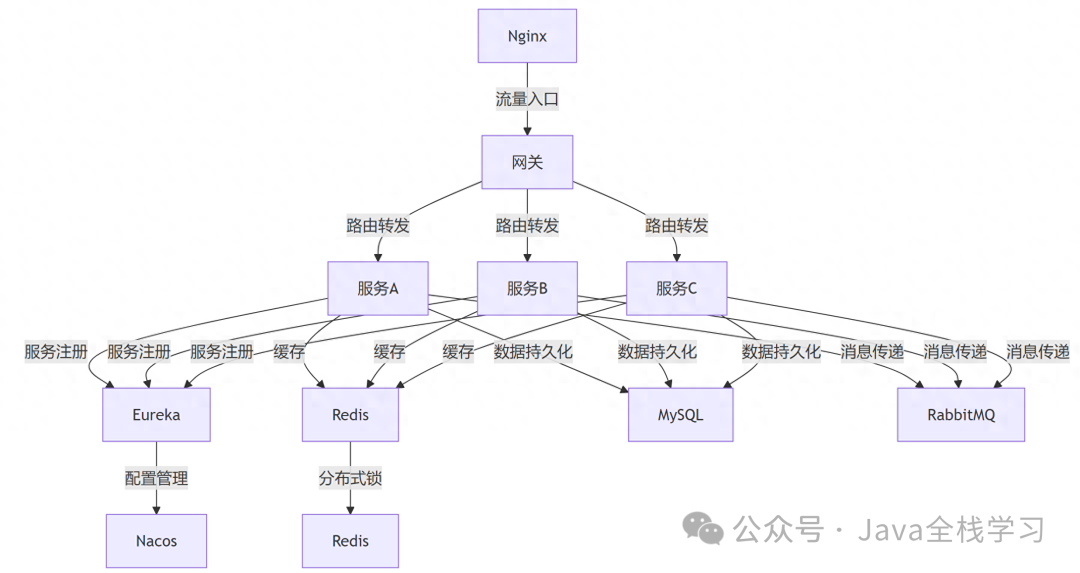
前言

没能一个月刷完力扣hot100，但还是要继续刷下去，记录一下每题的思路~

这次是普通数组相关的题目

（1）53. 最大子数组和

①暴力求出每种子数组和，超时

②动规，f(i+1)=max(nums[i]+f(i),nums[i])。

设f(i)为以i结尾的子串最大和，即ans=最大的f(i)，可得f(i+1)为nums[i+1]考虑加不加f(i)，取更大的结果。

滚动数组思想：用pre记录f(i-1)，f(i)=max(pre+nums[i],nums[i])，并用maxAns记录pre最大值，即为最终结果

class Solution {public int maxSubArray(int[] nums) {// 设f(i)为，以i结尾的子串最大和，即ans=最大的f(i)// 并且f(i+1)考虑为nums[i+1]考虑加不加f(i)，取更大的结果// 滚动数组思想：用pre记录f(i-1)，f(i)=max(pre+nums[i],nums[i])int pre=0, maxAns=nums[0];for(int n:nums){pre=Math.max(pre+n,n);maxAns=Math.max(maxAns,pre);}return maxAns;}
}

③前缀和。区间[l,r]和为preSum(r)-preSum[l]。

对于每个位置i的前缀和，记录前面最小前缀和minPreSum，即得该位置的最大区间和pre(i)-minPreSum，每次取最大即为结果

class Solution {public int maxSubArray(int[] nums) {int ans = Integer.MIN_VALUE, minPreSum=0, preSum=0;for(int n:nums){preSum+=n; // 前缀和ans = Math.max(ans,preSum-minPreSum); // 最大区间minPreSum = Math.min(minPreSum,preSum); // 最小前缀和}return ans;}
}

④分治法，类似线段树。

对每个节点维护l(l为左端点)、r(r为右端点)、m(区间最大和)、i(区间总和)四个变量。

深度遍历更新每个节点信息l=max(左l, 左i+右l)，r=max(右r, 右i+左r)，m=max(max(左m, 右m), 左r+右l)，i=左i+右i，最后返回根的m。

不仅可以解决区间 [0,n−1]，还可以用于解决任意的子区间 [l,r] 的问题

class Solution {public class Status{public int lSum,rSum,mSum,iSum;public Status(int lSum,int rSum,int mSum,int iSum){this.lSum=lSum; // l为左端点this.rSum=rSum; // r为右端点this.mSum=mSum; // 最大和this.iSum=iSum; // 总和}}public int maxSubArray(int[] nums) {return getInfo(nums,0,nums.length-1).mSum;}public Status getInfo(int[] a,int l,int r){if(l==r)return new Status(a[l],a[l],a[l],a[l]); // 叶节点// 分治int m = (l+r)>>1;Status lSub = getInfo(a,l,m);Status rSub = getInfo(a,m+1,r);return pushUp(lSub,rSub); // 更新信息}public Status pushUp(Status l,Status r){int iSum = l.iSum + r.iSum; // 总和int lSum = Math.max(l.lSum, l.iSum+r.lSum); // 左l，左i加右lint rSum = Math.max(r.rSum, r.iSum+l.rSum); // 右r，右i加左rint mSum = Math.max(Math.max(l.mSum,r.mSum), l.rSum+r.lSum); // 左右m，左r加右lreturn new Status(lSum,rSum,mSum,iSum);}
}

（2）56. 合并区间

排序合并。按左端点升序，用l、r记录当前处理区间；判断前后区间是否重合，重合则更新r，合并区间取右端点最大值；无重合就记录l、r并记录下一个区间。单独记录最后一种情况

class Solution {public int[][] merge(int[][] intervals) {List<int[]> res = new ArrayList<>();Arrays.sort(intervals,(a,b)->a[0]-b[0]); // 第一个元素升序int l=intervals[0][0], r=intervals[0][1];for(int i=1;i<intervals.length;i++){if(intervals[i][0]<=r)r=Math.max(r,intervals[i][1]); // 重合else{res.add(new int[]{l,r}); // 记录l=intervals[i][0];r=intervals[i][1];}}res.add(new int[]{l,r}); // 最后一种情况return res.toArray(new int[res.size()][]);}
}

（3）189. 轮转数组

①额外数组。逐个将nums中i位置，复制到ans的(i+k)%n位置，最后将ans用System.arraycopy复制到nums中

class Solution {public void rotate(int[] nums, int k) {int n =nums.length;int[] ans = new int[n];for(int i=0;i<n;i++)ans[(i+k)%n]=nums[i]; // 逐个拷贝System.arraycopy(ans,0,nums,0,n);}
}

②环形替换。使用temp记录下一个要替换的元素，会出现环形。

设走了a圈、处理了b个元素，即an=bk，为经过总元素为n、k的最小公倍数lcm=bk，遍历次数为n/b=nk/lcm=gcd最大公约数。

因此遍历gcd次，每次前后替换，直到回到起点，进行下一个环形

class Solution {public void rotate(int[] nums, int k) {int n=nums.length;k = k%n; // k小于n// 走了a圈、处理了b个元素，即an=bk，为经过总元素为n、k的最小公倍数lcm=bk// 遍历次数为n/b=nk/lcm=gcd最大公约数int count = gcd(k,n);for(int start=0; start<count; start++){int cur = start, pre = nums[start]; // 当前元素do{int next = (cur+k)%n, temp = nums[next]; // 下一个元素nums[next] = pre; // 更换pre = temp; // 更新precur = next; // 更新cur}while(start!=cur); // 若相等则回到起点}}// 最大公约数，欧几里得算法（辗转相除法）public int gcd(int x, int y){return y>0 ? gcd(y,x%y) : x;}
}

③如果理解不了最大公约数的，可以看看这个方法。环形替换，大致同上。

count记录已处理元素，当count为n时结束。start从0开始，每次前后替换，直到回到起点，进行下一个环形

class Solution {public void rotate(int[] nums, int k) {int n=nums.length;k = k%n; // k小于nint count = 0; // 处理元素总数for(int start=0; start<n; start++){ // 遍历次数不定int cur = start, pre = nums[start]; // 当前元素do{int next = (cur+k)%n, temp = nums[next]; // 下一个元素nums[next] = pre; // 更换pre = temp; // 更新precur = next; // 更新curif(++count==n)return; // 每个元素处理完}while(start!=cur); // 若相等则回到起点}}// 最大公约数，欧几里得算法（辗转相除法）public int gcd(int x, int y){return y>0 ? gcd(y,x%y) : x;}
}

④数组反转。先整体反转，再分别反转前k个和后n-k个，用双指针实现数组反转

class Solution {public void rotate(int[] nums, int k) {int n = nums.length;k %= n;reverse(nums,0,n-1); // 整体反转reverse(nums,0,k-1); // 前k个reverse(nums,k,n-1); // 后n-k个}public void reverse(int[] nums, int l, int r){ // 反转数组while(l<r){int temp = nums[l];nums[l++] = nums[r];nums[r--] = temp;}}
}

（4）238. 除自身以外数组的乘积

①前后缀乘积，不包括自己，其余元素乘积即前后缀乘积的乘积

class Solution {public int[] productExceptSelf(int[] nums) {int n = nums.length;int[] ans = new int[n];int[] prefix = new int[n], suffix = new int[n]; // 前后缀乘积prefix[0]=1; suffix[n-1]=1; // 初始化for(int i=1;i<n;i++){ // 计算prefix[i]=prefix[i-1]*nums[i-1];suffix[n-i-1]=suffix[n-i]*nums[n-i];}for(int i=0;i<n;i++) ans[i]=prefix[i]*suffix[i]; // 元素前后缀乘积return ans;}
}

②前后缀乘积，仅使用结果数组，先用ans记录前缀乘积，不包括自己，用suffix变量记录后缀乘积，不包括自己，从后遍历ans*=suffix

class Solution {public int[] productExceptSelf(int[] nums) {int n = nums.length;int[] ans = new int[n];ans[0]=1; // 初始化for(int i=1;i<n;i++) ans[i]=ans[i-1]*nums[i-1]; // 计算前缀乘积int suffix=1; // 后缀乘积for(int i=n-1;i>=0;i--){ // 计算后缀乘积和结果ans[i]*=suffix;suffix*=nums[i];}return ans;}
}

（5）41. 缺失的第一个正数

①排序，跳过非正数，target记录目标正数，一直往后匹配，注意跳过重复出现的数

class Solution {public int firstMissingPositive(int[] nums) {Arrays.sort(nums); // 排序int index = 0, target = 1, n = nums.length;while(index<n&&nums[index]<=0)index++; // 跳过非正数if(index==n) return 1;while(index<n&&nums[index]==target){ // 目标正数index++;while(index<n&&nums[index]==target)index++; // 跳过重复数target++;}return target;}
}

②哈希，记录长度为n的flag数组。

nums中1-n+1至少有个数不存在。对于nums中值在1-n范围的数，将flag对应下标位置设为true；遍历flag第一个为false的位置没出现，如果flag全为true，则n+1一定没出现

class Solution {public int firstMissingPositive(int[] nums) {int n = nums.length;boolean[] flag = new boolean[n]; // 标志位，1-n+1一定会少一个for(int num:nums) if(num>0&&num<=n)flag[num-1]=true; // 出现就设truefor(int i=0;i<n;i++)if(!flag[i])return i+1; // 没出现该数，返回return n+1; // 1-n都出现，n+1不存在}
}

③哈希，同上。

用nums作为flag，先将负数置为n+1；再将每个绝对值在0-n的数，对应的下标置为负数值，不改变绝对值；遍历nums，第一个为负数的值，对应下标的值为结果

class Solution {public int firstMissingPositive(int[] nums) {int n = nums.length;for(int i=0;i<n;i++) if(nums[i]<=0)nums[i]=n+1; // 负数置为n+1for(int num:nums) { // 将1-n范围的数，对应下标的值置为负数，标记该下标对应值出现num = Math.abs(num); // 之前可能被置为负数，要取绝对值if(num<=n)nums[num-1]=-Math.abs(nums[num-1]); // 只改为负数，不改变绝对值}for(int i=0;i<n;i++) if(nums[i]>0)return i+1;return n+1; // 1-n都出现，n+1不存在}
}

④置换。对于每个位置i的值t，若t在1-n之间且t-1位置的值不为t，交换i与t-1位置的值，并循环判断i位置是否要继续交换，直到遍历完

class Solution {public int firstMissingPositive(int[] nums) {int n = nums.length;for(int i=0;i<n;i++){ // 对于每个数int t = nums[i];// t在1-n范围，且t-1位置值不为twhile(t>0&&t<=n&&nums[t-1]!=t){ nums[i] = nums[t-1];nums[t-1] = t;t = nums[i]; // 新nums[i]可能还要交换，更新t值}}for(int i=0;i<n;i++) if(nums[i]!=i+1)return i+1;return n+1;}
}