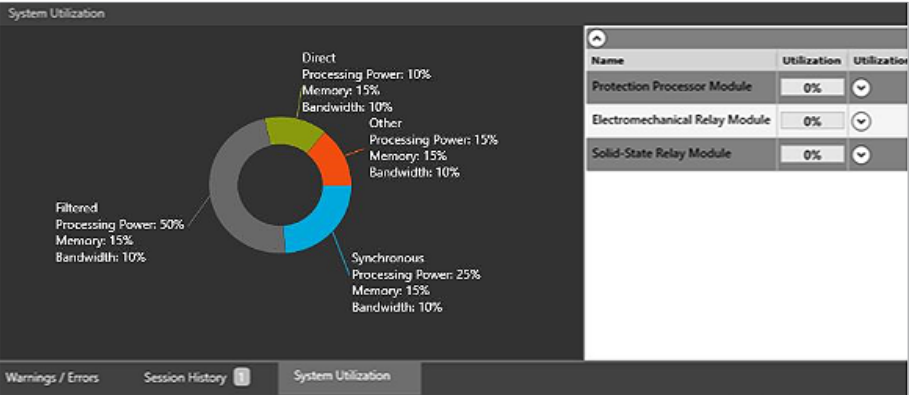
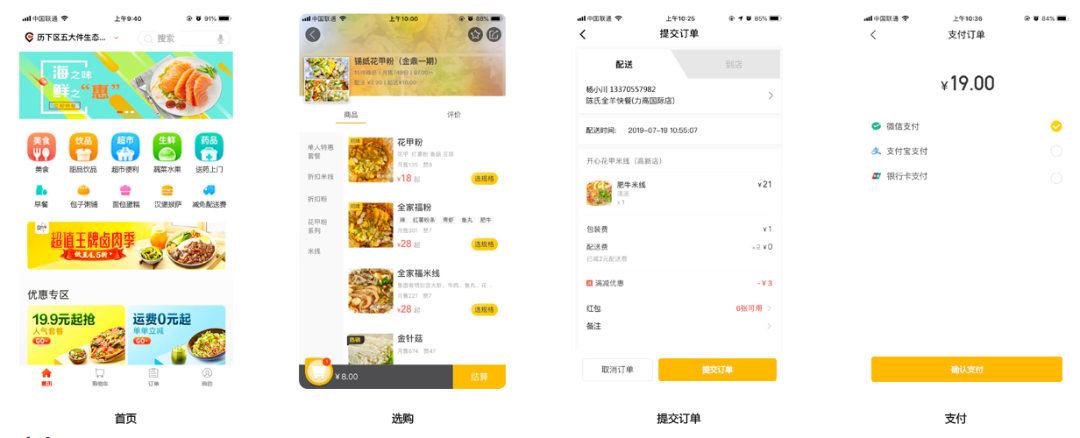
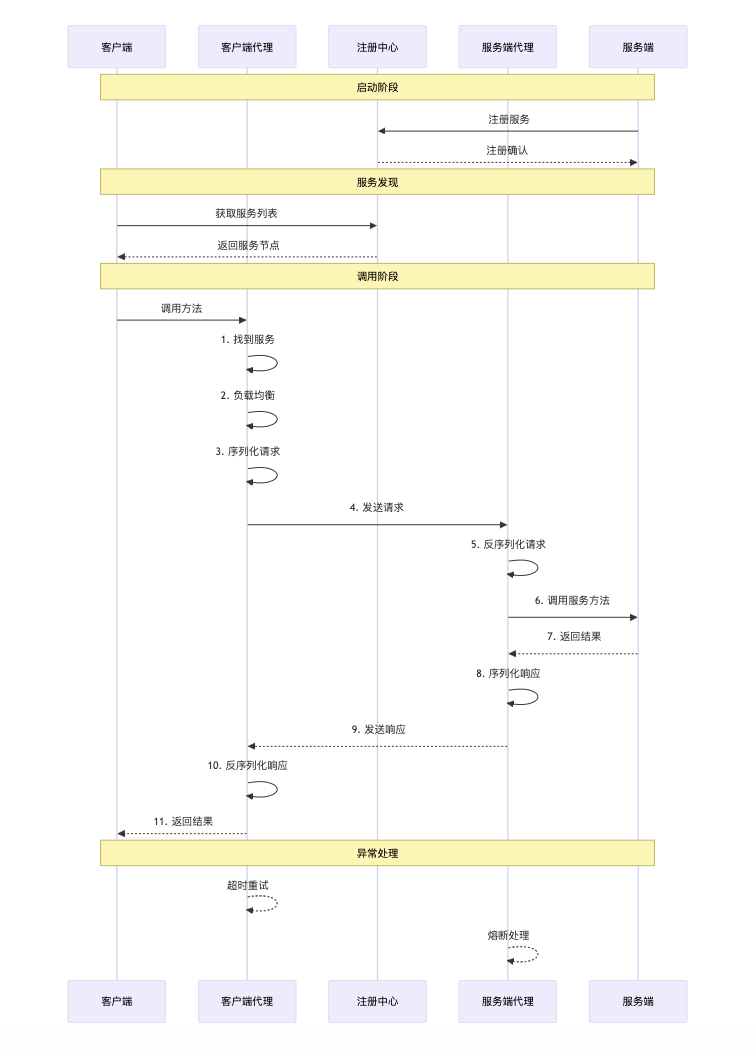
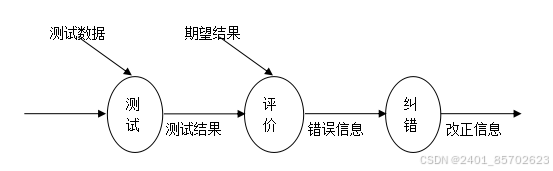
深度学习中做分类任务时，我们常常根据最后的全连接层得到一组向量A（比如：[0.9, 0.7, 0.2]），这组向量经过归一化得到向量B(比如：[0.5， 0.3， 0.2])，再根据B向量采用概率最大或者抽样的策略，最终为样本得到类别C（比如：[1, 0, 0]）。那么我们如何用数学语言来描述这种解的空间呢？下面基于聚类的解释可以参考。

背景描述

在这里，$c$ 表示聚类的类别数量，满足 $1<c<n$（即类别数量小于数据点总数 $n$，并且大于1）。接下来定义了三个集合，用于描述聚类标签表示的不同约束条件。

---

$E_{fcu}$ - 无约束标签空间

公式：
E f c u = { u ∈ R c ∣ u i ∈ [ 0 , 1 ] ∀ i } E_{fcu} = \{ \mathbf{u} \in \mathbb{R}^c \mid u_i \in [0, 1] \ \forall i \} Efcu​={u∈Rc∣ui​∈[0,1] ∀i}
含义：

• 这个集合表示一个 无约束标签空间。
• 向量 $\mathbf{u}$ 是 $c$ 维向量，属于欧几里得空间 ${\mathbb{R}}^c$。
• 每个分量 $u_i$ 的取值范围在 $[0,1]$。
• 不存在其他约束条件，所以称为 无约束。
• 几何上，这个集合是一个 单位超立方体，也就是一个在 ${\mathbb{R}}^c$ 空间中的正方体。

---

$E_{fc}$ - 有约束标签空间

公式：
E f c = { u ∈ E f c u ∣ ∑ i = 1 c u i = 1 } E_{fc} = \{ \mathbf{u} \in E_{fcu} \mid \sum_{i=1}^c u_i = 1 \} Efc​={u∈Efcu​∣i=1∑c​ui​=1}
含义：

• 这个集合表示一个 有约束标签空间。
• 它基于 $E_{fcu}$，但增加了一个约束条件：所有分量之和必须等于1（${\sum }_{i=1}^c{u}_i=1$）。
• 这个约束反映了 归一化的标签分布，例如在模糊聚类中，每个点被分配到各个聚类的隶属度之和等于1。
• 几何上，这个集合是 $E_{fcu}$ 内部的一个超平面，位于超立方体内。

---

$E_c$ - 硬标签空间

公式：
E c = { u ∈ E f c ∣ u i ∈ { 0 , 1 } ∀ i } E_c = \{ \mathbf{u} \in E_{fc} \mid u_i \in \{0, 1\} \ \forall i \} Ec​={u∈Efc​∣ui​∈{0,1} ∀i}
含义：

• 这个集合表示 硬标签空间，即非模糊标签。
• 它基于 $E_{fc}$，但进一步要求每个分量 $u_i$ 只能取 $0$ 或 $1$。
• 这种约束对应于硬聚类的情况：每个点只能属于一个类别，分量为1的位置表示点所属的类别。
• 几何上，这个集合是 $E_{fc}$ 的一个离散子集，表示欧几里得空间中的标准基向量集合。

---

几何解释

图1 展示了这些集合在三类情况下（$c=3$）的几何形状：

1. $E_c$ 是三类的标准基向量集合 $\{(1,0,0),(0,1,0),(0,0,1)\}$，每个点代表一个硬聚类标签。
2. $E_{fc}$ 是位于三维空间的一个平面（三角形的内部），这是超平面上的凸包，包含了模糊隶属度。
3. $E_{fcu}$ 是单位立方体，所有 $[0,1]$ 范围内的点都被包括。

---

术语总结

1. $E_{fcu}$ - 无约束的模糊标签空间，几何上是一个 $c$-维单位超立方体。
2. $E_{fc}$ - 加了总和为1约束的模糊标签空间，几何上是一个超平面的凸包。
3. $E_c$ - 硬标签空间，表示标准基向量集合。