当前位置：首页 > news >正文

28-29【动手学深度学习】批量归一化 + ResNet

news 2025/4/28 9:48:55

1. 批量归一化

1.1 原理

当神经网络比较深的时候会发现：数据在下面，损失函数在上面，这样会出现什么问题？

正向传递的时候，数据是从下往上一步一步往上传递
反向传递的时候，数据是从上面往下传递，这时候就会出现问题：梯度在上面的时候比较大，越到下面就越容易变小（因为是n个很小的数进行相乘，越到后面结果就越小，也就是说越靠近数据的，层的梯度就越小）
上面的梯度比较大，那么每次更新的时候上面的层就会不断地更新；但是下面层因为梯度比较小，所以对权重地更新就比较少，这样的话就会导致上面的收敛比较快，而下面的收敛比较慢，这样就会导致底层靠近数据的内容（网络所尝试抽取的网络底层的特征：简单的局部边缘、纹理等信息）变化比较慢，上层靠近损失的内容（高层语义信息）收敛比较快，所以每一次底层发生变化，所有的层都得跟着变（底层的信息发生变化就导致上层的权重全部白学了），这样就会导致模型的收敛比较慢

所以提出了假设：能不能在改变底部信息的时候，避免顶部不断的重新训练？（这也是批量归一化所考虑的问题）

$\varepsilon$ 是为了避免除以0

全连接层

通常，我们将批量规范化层置于全连接层中的仿射变换和激活函数之间。设全连接层的输入为x，权重参数和偏置参数分别为W和b，激活函数为ϕ，批量规范化的运算符为BN。那么，使用批量规范化的全连接层的输出的计算详情如下：

h=ϕ(BN(Wx+b)).

回想一下，均值和方差是在应用变换的"相同"小批量上计算的。

卷积层

同样，对于卷积层，我们可以在卷积层之后和非线性激活函数之前应用批量规范化。当卷积有多个输出通道时，我们需要对这些通道的“每个”输出执行批量规范化，每个通道都有自己的拉伸（scale）和偏移（shift）参数，这两个参数都是标量。假设我们的小批量包含m个样本，并且对于每个通道，卷积的输出具有高度p和宽度q。那么对于卷积层，我们在每个输出通道的m⋅p⋅q个元素上同时执行每个批量规范化。因此，在计算平均值和方差时，我们会收集所有空间位置的值，然后在给定通道内应用相同的均值和方差，以便在每个空间位置对值进行规范化。

批量归一化需要在激活函数之前，因为BN是线性的吗，而激活函数是非线性的

使用BN，可以增大学习率，因此可以加速收敛速度

预测过程中的批量规范化

正如我们前面提到的，批量规范化在训练模式和预测模式下的行为通常不同。首先，将训练好的模型用于预测时，我们不再需要样本均值中的噪声以及在微批次上估计每个小批次产生的样本方差了。其次，例如，我们可能需要使用我们的模型对逐个样本进行预测。一种常用的方法是通过移动平均估算整个训练数据集的样本均值和方差，并在预测时使用它们得到确定的输出。可见，和暂退法一样，批量规范化层在训练模式和预测模式下的计算结果也是不一样的。

1.2 代码

从零实现

import torch
from torch import nn
from d2l import torch as d2ldef batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):# 通过is_grad_enabled来判断当前模式是训练模式还是预测模式if not torch.is_grad_enabled():# 如果是在预测模式下，直接使用传入的移动平均所得的均值和方差X_hat = (X - moving_mean) / torch.sqrt(moving_var + eps)else:assert len(X.shape) in (2, 4)if len(X.shape) == 2:# 使用全连接层的情况，计算特征维上的均值和方差mean = X.mean(dim=0)var = ((X - mean) ** 2).mean(dim=0)else:# 使用二维卷积层的情况，计算通道维上（axis=1）的均值和方差。# 这里我们需要保持X的形状以便后面可以做广播运算mean = X.mean(dim=(0, 2, 3), keepdim=True)var = ((X - mean) ** 2).mean(dim=(0, 2, 3), keepdim=True)# 训练模式下，用当前的均值和方差做标准化X_hat = (X - mean) / torch.sqrt(var + eps)# 更新移动平均的均值和方差moving_mean = momentum * moving_mean + (1.0 - momentum) * meanmoving_var = momentum * moving_var + (1.0 - momentum) * varY = gamma * X_hat + beta  # 缩放和移位return Y, moving_mean.data, moving_var.data

创建一个正确的 BatchNorm 图层

class BatchNorm(nn.Module):# num_features：完全连接层的输出数量或卷积层的输出通道数。# num_dims：2表示完全连接层，4表示卷积层def __init__(self, num_features, num_dims):super().__init__()if num_dims == 2:shape = (1, num_features)else:shape = (1, num_features, 1, 1)# 参与求梯度和迭代的拉伸和偏移参数，分别初始化成1和0self.gamma = nn.Parameter(torch.ones(shape))self.beta = nn.Parameter(torch.zeros(shape))# 非模型参数的变量初始化为0和1self.moving_mean = torch.zeros(shape)self.moving_var = torch.ones(shape)def forward(self, X):# 如果X不在内存上，将moving_mean和moving_var# 复制到X所在显存上if self.moving_mean.device != X.device:self.moving_mean = self.moving_mean.to(X.device)self.moving_var = self.moving_var.to(X.device)# 保存更新过的moving_mean和moving_varY, self.moving_mean, self.moving_var = batch_norm(X, self.gamma, self.beta, self.moving_mean,self.moving_var, eps=1e-5, momentum=0.9)return Y

应用BatchNorm 于LeNet模型

net = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5), BatchNorm(6, num_dims=4),nn.Sigmoid(), nn.MaxPool2d(kernel_size=2, stride=2),nn.Conv2d(6, 16,kernel_size=5), BatchNorm(16, num_dims=4),nn.Sigmoid(), nn.MaxPool2d(kernel_size=2, stride=2),nn.Flatten(), nn.Linear(16 * 4 * 4, 120),BatchNorm(120, num_dims=2), nn.Sigmoid(),nn.Linear(120, 84), BatchNorm(84, num_dims=2),nn.Sigmoid(), nn.Linear(84, 10))

在Fashion-MNIST数据集上训练网络

lr, num_epochs, batch_size = 1.0, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

拉伸参数 gamma 和偏移参数 beta

net[1].gamma.reshape((-1, )), net[1].beta.reshape((-1, ))

简明实现

net = nn.Sequential(nn.Conv2d(1, 6, kernel_size=5), nn.BatchNorm2d(6),nn.Sigmoid(), nn.MaxPool2d(kernel_size=2, stride=2),nn.Conv2d(6, 16, kernel_size=5), nn.BatchNorm2d(16),nn.Sigmoid(), nn.MaxPool2d(kernel_size=2, stride=2),nn.Flatten(), nn.Linear(256, 120), nn.BatchNorm1d(120),nn.Sigmoid(), nn.Linear(120, 84), nn.BatchNorm1d(84),nn.Sigmoid(), nn.Linear(84, 10))

d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

小结

在模型训练过程中，批量规范化利用小批量的均值和标准差，不断调整神经网络的中间输出，使整个神经网络各层的中间输出值更加稳定。
批量规范化在全连接层和卷积层的使用略有不同。
批量规范化层和暂退层一样，在训练模式和预测模式下计算不同。
批量规范化有许多有益的副作用，主要是正则化。另一方面，”减少内部协变量偏移“的原始动机似乎不是一个有效的解释。

2. ResNet

2.1 原理

只有当较复杂的函数类包含较小的函数类时，我们才能确保提高它们的性能。对于深度神经网络，如果我们能将新添加的层训练成恒等映射（identity function）f(x)=x，新模型和原模型将同样有效。同时，由于新模型可能得出更优的解来拟合训练数据集，因此添加层似乎更容易降低训练误差。

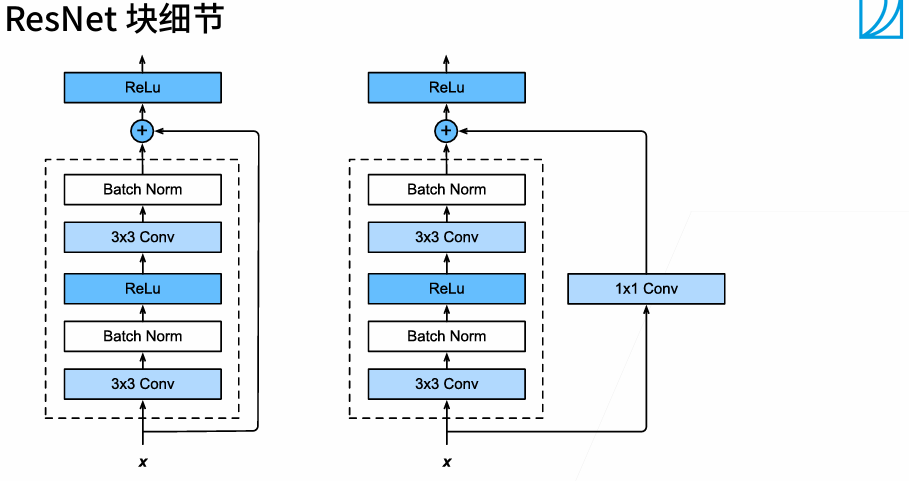
当经过很多层卷积之后，可能通道数会产生变化，所以要加上1×1的卷积转换通道数。（通常情况下是，当高宽减半时，通道数变为原来的一倍）

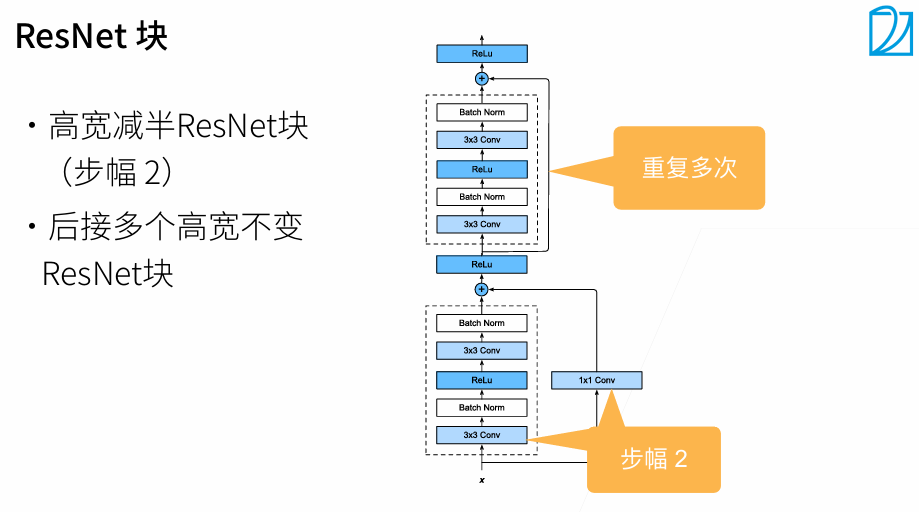
2.2 代码

残差块

import torch 
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2lclass Residual(nn.Module):def __init__(self, input_channels, num_channels, use_1x1conv=False, strides=1):super().__init__()self.conv1 = nn.Conv2d(input_channels, num_channels, kernel_size=3,padding=1, stride=strides)self.conv2 = nn.Conv2d(num_channels, num_channels, kernel_size=3,padding=1)if use_1x1conv:self.conv3 = nn.Conv2d(input_channels, num_channels,kernel_size=1, stride=strides)else:self.conv3 = Noneself.bn1 =  nn.BatchNorm2d(num_channels)self.bn2 = nn.BatchNorm2d(num_channels)# 当 inplace=True 时，ReLU 会直接在输入张量上修改数据（覆盖原值），不分配额外内存存储输出self.relu = nn.ReLU(inplace=True)  def forward(self, X):Y = F.relu(self.bn1(self.conv1(X)))Y = self.bn2(self.conv2(Y))if self.conv3:X = self.conv3(X)Y = Y + Xreturn F.relu(Y)

输入和输出形状一致

blk = Residual(3, 3)
X = torch.rand(4, 3, 6, 6)
Y = blk(X)
Y.shape

增加输出通道数的同时，减半输出的高和宽

blk = Residual(3, 6, use_1x1conv=True, strides=2)
blk(X).shape

ResNet模型

b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3),nn.BatchNorm2d(64), nn.ReLU(),nn.MaxPool2d(kernel_size=3, stride=2, padding=1))def resnet_block(input_channels, num_channels, num_residuals,first_block=False):blk = []for i in range(num_residuals):if i == 0 and not first_block:blk.append(Residual(input_channels, num_channels, use_1x1conv=True,strides=2))else:blk.append(Residual(num_channels, num_channels))return blk# *的含义是将list展开，变成一个个的输入
b2 = nn.Sequential(*resnet_block(64, 64, 2, first_block=True))
b3 = nn.Sequential(*resnet_block(64, 128, 2))
b4 = nn.Sequential(*resnet_block(128, 256, 2))
b5 = nn.Sequential(*resnet_block(256, 512, 2))net = nn.Sequential(b1, b2, b3, b4, b5, nn.AdaptiveAvgPool2d((1, 1)),nn.Flatten(), nn.Linear(512, 10))

观察一下ResNet中不同模块的输入形状是如何变化的

X = torch.rand(size=(1, 1, 224, 224))
for layer in net:X = layer(X)print(layer.__class__.__name__, 'output shape:\t', X.shape)

训练模型

lr, num_epochs, batch_size = 0.05, 10, 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=96)
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())

小结

学习嵌套函数（nested function）是训练神经网络的理想情况。在深层神经网络中，学习另一层作为恒等映射（identity function）较容易（尽管这是一个极端情况）。
残差映射可以更容易地学习同一函数，例如将权重层中的参数近似为零。
利用残差块（residual blocks）可以训练出一个有效的深层神经网络：输入可以通过层间的残余连接更快地向前传播。
残差网络（ResNet）对随后的深层神经网络设计产生了深远影响。

ResNet的梯度计算