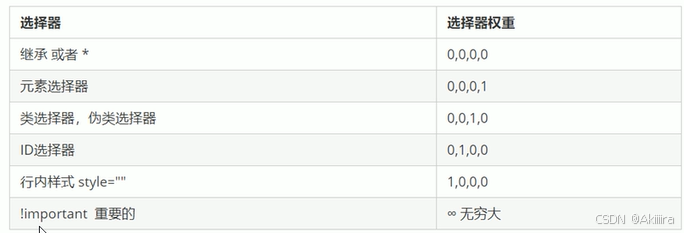
5. 微分中值定理及其应用
5.1 微分中值定理
5.1.1 极值与极值点
【定义5.1.1】 f ( x ) f(x) f(x)定义域为 ( a , b ) (a,b) (a,b), x 0 ∈ ( a , b ) x_0\in(a,b) x0∈(a,b),若 ∃ O ( x 0 , ρ ) ⊂ ( a , b ) \exists O(x_0,\rho)\subset(a,b) ∃O(x0,ρ)⊂(a,b),使得 f ( x ) ≤ f ( x 0 ) , x ∈ O ( x 0 , ρ ) f(x)\le f(x_0),x\in O(x_0,\rho) f(x)≤f(x0),x∈O(x0,ρ)(以 x 0 x_0 x0为中心, ρ \rho ρ为半径的邻域),则称 x 0 x_0 x0是 f ( x ) f(x) f(x)的一个极大值点, f ( x 0 ) f(x_0) f(x0)是一个极大值。
f ( x ) f(x) f(x)定义域为 ( a , b ) (a,b) (a,b), x 0 ∈ ( a , b ) x_0\in(a,b) x0∈(a,b),若 ∃ O ( x 0 , ρ ) ⊂ ( a , b ) \exists O(x_0,\rho)\subset(a,b) ∃O(x0,ρ)⊂(a,b),使得 f ( x ) ≥ f ( x 0 ) , x ∈ O ( x 0 , ρ ) f(x)\ge f(x_0),x\in O(x_0,\rho) f(x)≥f(x0),x∈O(x0,ρ)(以 x 0 x_0 x0为中心, ρ \rho ρ为半径的邻域),则称 x 0 x_0 x0是 f ( x ) f(x) f(x)的一个极小值点, f ( x 0 ) f(x_0) f(x0)是一个极小值。
极大值点和极小值点统称极值点,极大值和极小值统称极值。
(1)极值是局部概念。

极小值可以大于极大值,比如上图 x 0 x_0 x0是极大值点, x 1 x_1 x1是极小值点,但是 x 1 x_1 x1对应的极小值大于 x 0 x_0 x0对应的极大值
(2)极值点可以有无穷多个,比如 y = sin 1 x y=\sin\frac{1}{x} y=sinx1, x = 1 n π + π 2 , n x=\frac{1}{n\pi+\frac{\pi}{2}},n x=nπ+2π1,n是偶数,对应极大值点, n n n是奇数对应极小值点。
(3)极致概念与连续和可导等概念无关。
【定理5.1.1】【Fermat(费马)引理】设 x 0 x_0 x0是 f ( x ) f(x) f(x)的一个极值点,若 f ( x ) f(x) f(x)在 x 0 x_0 x0可导,则 f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0.
【证】不妨设 x 0 x_0 x0是极大值点,在 x 0 x_0 x0的某一邻域中,
若 x < x 0 , f ( x ) ≤ f ( x 0 ) , f ( x ) − f ( x 0 ) x − x 0 ≥ 0 x<x_0,f(x)\le f(x_0),\frac{f(x)-f(x_0)}{x-x_0}\ge 0 x<x0,f(x)≤f(x0),x−x0f(x)−f(x0)≥0,
若 x > x 0 , f ( x ) ≤ f ( x 0 ) , f ( x ) − f ( x 0 ) x − x 0 ≤ 0 x>x_0,f(x)\le f(x_0),\frac{f(x)-f(x_0)}{x-x_0}\le 0 x>x0,f(x)≤f(x0),x−x0f(x)−f(x0)≤0,
由于 f ( x ) f(x) f(x)在 x 0 x_0 x0可导,则 f ′ ( x 0 ) = f + ′ ( x 0 ) = f − ′ ( x 0 ) f'(x_0)=f'_+(x_0)=f'_-(x_0) f′(x0)=f+′(x0)=f−′(x0)
f − ′ ( x 0 ) = lim x → x 0 − f ( x ) − f ( x 0 ) x − x 0 ≥ 0 f'_-(x_0)=\lim\limits_{x\to x_0^-}\frac{f(x)-f(x_0)}{x-x_0}\ge 0 f−′(x0)=x→x0−limx−x0f(x)−f(x0)≥0
f − ′ ( x 0 ) = lim x → x 0 + f ( x ) − f ( x 0 ) x − x 0 ≤ 0 f'_-(x_0)=\lim\limits_{x\to x_0^+}\frac{f(x)-f(x_0)}{x-x_0}\le 0 f−′(x0)=x→x0+limx−x0f(x)−f(x0)≤0
由于 f ′ ( x 0 ) = f + ′ ( x 0 ) = f − ′ ( x 0 ) f'(x_0)=f'_+(x_0)=f'_-(x_0) f′(x0)=f+′(x0)=f−′(x0)
所以 f ′ ( x 0 ) = 0 f'(x_0)=0 f′(x0)=0
证毕.
【注】某点导数为0,不一定在该点取到极值,比如 y = x 3 , y ′ = 3 x 2 y=x^3,y'=3x^2 y=x3,y′=3x2,导数为0的点是 x = 0 x=0 x=0,但是根据图形,它在 x = 0 x=0 x=0这一点不是极值点。

5.1.2 Rolle(罗尔)定理
【定理5.1.2】【Rolle(罗尔)定理】 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]连续,在 ( a , b ) (a,b) (a,b)可导, f ( a ) = f ( b ) f(a)=f(b) f(a)=f(b),则至少存在一个 ξ ∈ ( a , b ) \xi\in(a,b) ξ∈(a,b),使得 f ′ ( ξ ) = 0 f'(\xi)=0 f′(ξ)=0.
【证】 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]连续,则 f ( x ) f(x) f(x)一定在 [ a , b ] [a,b] [a,b]上取到最大值 M M M,最小值 m m m
不妨设 ξ , η ∈ [ a , b ] \xi,\eta\in[a,b] ξ,η∈[a,b], f ( ξ ) = M , f ( η ) = m f(\xi)=M,f(\eta)=m f(ξ)=M,f(η)=m
(1)若 m = M , f ( x ) = C , C m=M,f(x)=C,C m=M,f(x)=C,C为常数,定理结论成立;
(2)若 M > m M>m M>m,则 M , m M,m M,m中有一个不等于 f ( a ) ( = f ( b ) ) f(a)(=f(b)) f(a)(=f(b)),即最大值、最小值至少有一个在区间内部取到,若不然,最大值、最小值都在端点取到,推出 m = M m=M m=M矛盾,不妨设 M = f ( ξ ) > f ( a ) = f ( b ) M=f(\xi)>f(a)=f(b) M=f(ξ)>f(a)=f(b)( M M M在内部取到), ξ ∈ ( a , b ) , ξ \xi\in(a,b),\xi ξ∈(a,b),ξ是 f ( x ) f(x) f(x)的一个极大值点,由于 f ( x ) f(x) f(x)在 ( a , b ) (a,b) (a,b)可导,则 f ( x ) f(x) f(x)在 ξ \xi ξ可导,由费马引理, f ′ ( ξ ) = 0 f'(\xi)=0 f′(ξ)=0
【注】要用中值定理,首先的要求是闭区间连续开区间可导。
【罗尔定理的几何意义】满足定理条件的函数一定在某一点存在一条与 x x x轴平行,亦即与曲线的两个端点的连线平行的切线。

【例5.1.1】【Legendre(勒让德)多项式】 P n ( x ) = 1 2 n ⋅ n ! ⋅ d n d x n ( x 2 − 1 ) n P_n(x)=\frac{1}{2^n\cdot n!}\cdot\frac{d^n}{dx^n}(x^2-1)^n Pn(x)=2n⋅n!1⋅dxndn(x2−1)n, ( x 2 − 1 ) n (x^2-1)^n (x2−1)n是 2 n 2n 2n次多项式,它算 n n n阶导数后就变成 n n n次多项式,即勒让德多项式是 n n n次多项式,证明:它在 ( − 1 , 1 ) (-1,1) (−1,1)有 n n n个不同的根。
【证】 ( x 2 − 1 ) n (x^2-1)^n (x2−1)n的根是 − 1 , 1 -1,1 −1,1,
由于 ( x 2 − 1 ) n (x^2-1)^n (x2−1)n在闭区间连续开区间 ( − 1 , 1 ) (-1,1) (−1,1)可导,且在 − 1 -1 −1和 1 1 1点的函数值相等都是0,由罗尔定理可知, ∃ x 11 \exists x_{11} ∃x11在对应开区间 ( − 1 , 1 ) (-1,1) (−1,1)内,使得 d d x ( x 2 − 1 ) n ∣ x = x 11 = 0 \frac{d}{dx}(x^2-1)^n|_{x=x_{11}}=0 dxd(x2−1)n∣x=x11=0
d d x ( x 2 − 1 ) n = n ( x 2 − 1 ) n − 1 ⋅ 2 x \frac{d}{dx}(x^2-1)^n=n(x^2-1)^{n-1}\cdot 2x dxd(x2−1)n=n(x2−1)n−1⋅2x的根有 − 1 , 1 -1,1 −1,1,还有 x 11 x_{11} x11(导数等于0的点,刚才的罗尔定理),这下三个点函数值相等为0,三个点中两两中间有个导数为0的点(罗尔定理)
d 2 d x 2 ( x 2 − 1 ) n \frac{d^2}{dx^2}(x^2-1)^n dx2d2(x2−1)n包含因子 ( x 2 − 1 ) n − 2 (x^2-1)^{n-2} (x2−1)n−2,则它还是有 − 1 , 1 -1,1 −1,1这两个根,还有 x 21 , x 22 x_{21},x_{22} x21,x22(同上)
……
设 m < n m<n m<n, d m d x m ( x 2 − 1 ) n \frac{d^m}{dx^m}(x^2-1)^n dxmdm(x2−1)n包含因子 ( x 2 − 1 ) n − m (x^2-1)^{n-m} (x2−1)n−m,则它还是有 − 1 , 1 -1,1 −1,1这两个根,还有 x m 1 , . . . , x m m x_{m1},...,x_{mm} xm1,...,xmm这 m m m个零点(同上)
到 d n − 1 d x n − 1 ( x 2 − 1 ) n \frac{d^{n-1}}{dx^{n-1}}(x^2-1)^n dxn−1dn−1(x2−1)n包含因子 ( x 2 − 1 ) (x^2-1) (x2−1),则它还是有 − 1 , 1 -1,1 −1,1这两个根,还有 n − 1 n-1 n−1个零点,即 x n − 1 , 1 , . . . , x n − 1 , n − 1 x_{n-1,1},...,x_{n-1,n-1} xn−1,1,...,xn−1,n−1
d n d x n ( x 2 − 1 ) n \frac{d^n}{dx^n}(x^2-1)^n dxndn(x2−1)n在 ( − 1 , 1 ) (-1,1) (−1,1)中有 n n n个零点(上面罗尔定理推过来的),但是没有 − 1 , 1 -1,1 −1,1这两个根,因为求导把 ( x 2 − 1 ) n (x^2-1)^n (x2−1)n求成了常数(参考高阶导数那节课)
所以它在 ( − 1 , 1 ) (-1,1) (−1,1)有 n n n个不同的根。
证毕。
5.1.3 Lagrange(拉格朗日)中值定理
【定理5.1.3】【Lagrange(拉格朗日)中值定理】【罗尔定理的推广】 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]连续,在 ( a , b ) (a,b) (a,b)可导,则 ∃ ξ ∈ ( a , b ) \exists \xi \in(a,b) ∃ξ∈(a,b),使得 f ′ ( ξ ) = f ( b ) − f ( a ) b − a f'(\xi)=\frac{f(b)-f(a)}{b-a} f′(ξ)=b−af(b)−f(a).
【注】上述形式换写法:
- f ( b ) − f ( a ) = f ′ ( ξ ) ( b − a ) , ξ = a + θ ( b − a ) , θ ∈ ( 0 , 1 ) f(b)-f(a)=f'(\xi)(b-a),\xi=a+\theta(b-a),\theta\in(0,1) f(b)−f(a)=f′(ξ)(b−a),ξ=a+θ(b−a),θ∈(0,1),即写成 f ( b ) − f ( a ) = f ′ ( a + θ ( b − a ) ) ( b − a ) , θ ∈ ( 0 , 1 ) f(b)-f(a)=f'(a+\theta(b-a))(b-a),\theta\in(0,1) f(b)−f(a)=f′(a+θ(b−a))(b−a),θ∈(0,1)
- 记 a = x , b = x + Δ x , b − a = Δ x , f ( x + Δ x ) − f ( x ) = f ′ ( x + θ Δ x ) Δ x , Δ x a=x,b=x+\Delta x,b-a=\Delta x,f(x+\Delta x)-f(x)=f'(x+\theta \Delta x)\Delta x,\Delta x a=x,b=x+Δx,b−a=Δx,f(x+Δx)−f(x)=f′(x+θΔx)Δx,Δx可正可负
- Δ y = f ′ ( x + θ Δ x ) Δ x \Delta y=f'(x+\theta \Delta x)\Delta x Δy=f′(x+θΔx)Δx
【几何解释】
f ( b ) − f ( a ) b − a \frac{f(b)-f(a)}{b-a} b−af(b)−f(a)是在 ( a , b ) (a,b) (a,b)区间端点连线的这条弦的斜率,所以 ξ \xi ξ这点的切线和这条弦平行。
【证】令 φ ( x ) = f ( x ) − f ( a ) − f ( b ) − f ( a ) b − a ( x − a ) \varphi(x)=f(x)-f(a)-\frac{f(b)-f(a)}{b-a}(x-a) φ(x)=f(x)−f(a)−b−af(b)−f(a)(x−a)
则 φ ( x ) \varphi(x) φ(x)在 [ a , b ] [a,b] [a,b]连续, ( a , b ) (a,b) (a,b)可导,
φ ( a ) = 0 , φ ( b ) = 0 = φ ( a ) \varphi(a)=0,\varphi(b)=0=\varphi(a) φ(a)=0,φ(b)=0=φ(a),由罗尔定理可知 ∃ ξ ∈ ( a , b ) \exists \xi \in (a,b) ∃ξ∈(a,b),使得 φ ′ ( ξ ) = 0 \varphi'(\xi)=0 φ′(ξ)=0, φ ′ ( x ) = f ′ ( x ) − f ( b ) − f ( a ) b − a \varphi'(x)=f'(x)-\frac{f(b)-f(a)}{b-a} φ′(x)=f′(x)−b−af(b)−f(a)
φ ′ ( ξ ) = f ′ ( ξ ) − f ( b ) − f ( a ) b − a = 0 \varphi'(\xi)=f'(\xi)-\frac{f(b)-f(a)}{b-a}=0 φ′(ξ)=f′(ξ)−b−af(b)−f(a)=0
即 f ′ ( ξ ) = f ( b ) − f ( a ) b − a f'(\xi)=\frac{f(b)-f(a)}{b-a} f′(ξ)=b−af(b)−f(a)
用拉格朗日中值定理讨论函数性质
【例】已知 f ( x ) = c , c f(x)=c,c f(x)=c,c为常数 ⇒ f ′ ( x ) ≡ 0 \Rightarrow f'(x)\equiv 0 ⇒f′(x)≡0 f ( x ) = c , c f(x)=c,c f(x)=c,c为常数,证明: ⇐ f ′ ( x ) ≡ 0 \Leftarrow f'(x)\equiv 0 ⇐f′(x)≡0
【证】设 f ( x ) , x ∈ ( a , b ) , ∀ x 1 , x 2 ∈ ( a , b ) , f ( x 2 ) − f ( x 1 ) = f ′ ( ξ ) ( x 2 − x 1 ) f(x),x\in(a,b),\forall x_1,x_2\in(a,b),f(x_2)-f(x_1)=f'(\xi)(x_2-x_1) f(x),x∈(a,b),∀x1,x2∈(a,b),f(x2)−f(x1)=f′(ξ)(x2−x1)(拉格朗日中值定理)
由于 f ′ ( ξ ) = 0 f'(\xi)=0 f′(ξ)=0所以 f ( x 1 ) = f ( x 2 ) , ∀ x 1 , x 2 ∈ ( a , b ) f(x_1)=f(x_2),\forall x_1,x_2\in(a,b) f(x1)=f(x2),∀x1,x2∈(a,b)
即 f ( x ) = c , c f(x)=c,c f(x)=c,c为常数