机器人中的数值优化|【六】线性共轭梯度法,牛顿共轭梯度法
往期回顾
机器人中的数值优化|【一】数值优化基础
机器人中的数值优化|【二】最速下降法,可行牛顿法的python实现,以Rosenbrock function为例
机器人中的数值优化|【三】无约束优化,拟牛顿法理论与推导
机器人中的数值优化|【四】L-BFGS理论推导与延伸
机器人中的数值优化|【五】BFGS算法非凸/非光滑处理
关于牛顿-共轭梯度法,笔者认为对其最直接和最根本的认识,这篇帖子写得特别好,可以参考東雲正樹的 如何理解共轭梯度法 一文。
为什么要用Conjugate Gradient method?
从前面的系列我们知道,对于一个凸的无约束优化,我们总是希望通过梯度,基于这样那样的方法来到达最优点。在前面基本的梯度下降方法中,我们每次计算一个梯度,并根据线性搜索得到的一个较为不错的步长,向前优化一步。在Newton-CG method中我们不禁要提问了:有没有一种可以有确定的搜索次数,而且次数还比较少的方法呢?这个方法就是Newton-CG method。我们知道在向量中存在标准正交集的概念,在优化问题中,我们也存在共轭梯度的概念,关于共轭梯度的具体定义和推导可以进一步查阅相关的资料。本质上,就是把原来随机走梯度的过程,变为在凸问题空间中“正交”的梯度向量上,每个向量只走一步,且是最优的一步的过程。
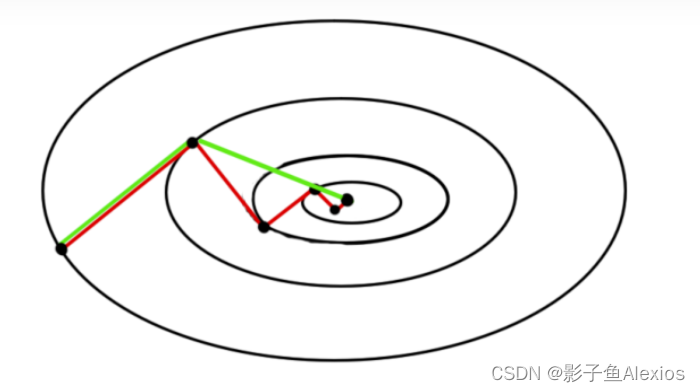
从上面的例子我们可以看到,绿色为共轭梯度法,红色为梯度下降法,我们其实要做的工作就是在椭圆的切向和法向各走“最优”的一步,一步到位即可。
Gram-Schmitd正交化/施密特正交化
理解共轭梯度法,首先我们要回顾一个东西,那就是施密特正交化。利用施密特正交化,我们可以从空间中的一组向量得到互相正交的一组向量集。如果我们有一组互不平行的向量 [ α 1 , α 2 , α 3 , α 4 , α 5 , . . . ] {[\alpha_1, \alpha_2, \alpha_3, \alpha_4, \alpha_5,...]} [α1,α2,α3,α4,α5,...],利用一下公式可以得到正交基:
β 1 = α 1 \beta_1 = \alpha_1 β1=α1
β 2 = α 2 − ( β 1 , α 2 ) ( β 1 , β 1 ) β 1 \beta_2 = \alpha_2 - \frac{(\beta_1, \alpha_2)}{(\beta_1, \beta_1)} \beta_1 β2=α2−(β1,β1)(β1,α2)β1
β 3 = α 3 − ( β 1 , α 3 ) ( β 1 , β 1 ) β 1 − ( β 2 , α 3 ) ( β 2 , β 2 ) β 2 \beta_3 = \alpha_3 - \frac{(\beta_1, \alpha_3)}{(\beta_1, \beta_1)} \beta_1 - \frac{(\beta_2, \alpha_3)}{(\beta_2, \beta_2)} \beta_2 β3=α3−(β1,β1)(β1,α3)β1−(β2,β2)(β2,α3)β2
β 4 = α 4 − ( β 1 , α 4 ) ( β 1 , β 1 ) β 1 − ( β 2 , α 4 ) ( β 2 , β 2 ) β 2 − ( β 3 , α 4 ) ( β 3 , β 3 ) β 3 \beta_4 = \alpha_4 - \frac{(\beta_1, \alpha_4)}{(\beta_1, \beta_1)} \beta_1 - \frac{(\beta_2, \alpha_4)}{(\beta_2, \beta_2)} \beta_2 - \frac{(\beta_3, \alpha_4)}{(\beta_3, \beta_3)} \beta_3 β4=α4−(β1,β1)(β1,α4)β1−(β2,β2)(β2,α4)β2−(β3,β3)(β3,α4)β3
. . . ... ...
线性共轭梯度法
对于如下的一个问题
a r g m i n x f ( x ) = 1 2 x T A x − b T x argmin_x f(x) = \frac{1}{2}x^TAx - b^Tx argminxf(x)=21xTAx−bTx
我们要求其无约束优化。这里我们可以引入共轭梯度的概念,其概念类似于正交向量,对于一个正交向量 u , v u,v u,v,有 u T v = 0 u^Tv =0 uTv=0。一个矩阵 A A A,如果存在向量 u , v u,v u,v,有 u T A v = 0 u^TAv=0 uTAv=0,则我们认为 u , v u,v u,v关于 A A A共轭。在下降过程中,如果我们每一步选择的下降方向都是一个独立的共轭向量,且一共有 n n n个共轭向量,则最多需要 n n n步即可下降到最优点。
回顾优化过程,最核心的公式为
x k + 1 = x k + α u k x_{k+1} = x_k + \alpha u_k xk+1=xk+αuk
其中 u k u_k uk为下降方向, α \alpha α为步长。将 x k + 1 x_{k+1} xk+1代入最优化目标公式,我们有
a r g m i n x f ( x k + 1 ) = a r g m i n x f ( x k + α u k ) argmin_x f(x_{k+1}) = argmin_x f(x_k + \alpha u_k) argminxf(xk+1)=argminxf(xk+αuk)
假设下降方向已经确定了,我们要确定最优步长
a r g m i n x f ( x k + α u k ) = a r g m i n x 1 2 ( x k + α u k ) T A ( x k + α u k ) − b T ( x k + α u k ) argmin_x f(x_k + \alpha u_k) = argmin_x \frac{1}{2}(x_k + \alpha u_k)^TA(x_k + \alpha u_k) - b^T(x_k + \alpha u_k) argminxf(xk+αuk)=argminx21(xk+αuk)TA(xk+αuk)−bT(xk+αuk)
对 α \alpha α求导,有
a r g m i n x f ′ ( x k + α u k ) = 0 argmin_x f'(x_k + \alpha u_k) = 0 argminxf′(xk+αuk)=0
解得
α = b T u k − x k T A u k u k T A u k \alpha = \frac{b^Tu_k - x_k^TAu_k}{u_k^TAu_k} α=ukTAukbTuk−xkTAuk
这里的 α \alpha α是最优步长的一个“尺度”,也就是scalar。那么问题来了,我们想要每次下降都能够是共轭方向的,怎么办呢?
设每次迭代之后的误差量为
r k = A x k − b r_k = Ax_k - b rk=Axk−b
令
u k = − r k + β k u k − 1 u_k = -r_k + \beta_k u_{k-1} uk=−rk+βkuk−1
两边乘以 u k − 1 T A u_{k-1}^TA uk−1TA有
u k − 1 T A u k = − u k − 1 T A r k + u k − 1 T A β k u k − 1 u_{k-1}^TAu_{k} = -u_{k-1}^TAr_k + u_{k-1}^TA\beta_ku_{k-1} uk−1TAuk=−uk−1TArk+uk−1TAβkuk−1
因为我们想要得到的是共轭方向,所以认为 u k − 1 T A u k = 0 u_{k-1}^TAu_{k} =0 uk−1TAuk=0
− u k − 1 T A r k + u k − 1 T A β k u k − 1 = 0 -u_{k-1}^TAr_k + u_{k-1}^TA\beta_ku_{k-1} = 0 −uk−1TArk+uk−1TAβkuk−1=0
β k = r k T A u k − 1 u k − 1 T A u k − 1 \beta_k= \frac{r_k^T A u_{k-1}}{u_{k-1}^TAu_{k-1}} βk=uk−1TAuk−1rkTAuk−1
在这里我们就可以得到一个缩放标量 β k \beta_k βk可以迭代计算共轭向量,最后得到的算法如下所示

优化线性共轭梯度法
进一步的,我们可以提出更高效的线性共轭梯度法。首先引入一些定理(这里的 p p p就是 u u u)

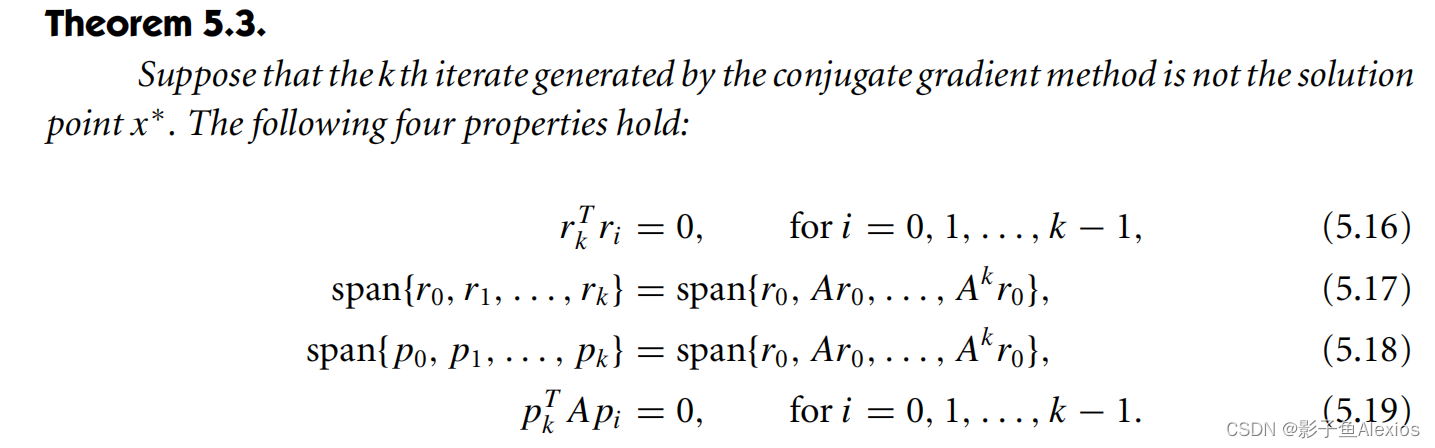
根据前面的公式,有
α = b T u k − x k T A u k u k T A u k = − r k T u k u k T A u k \alpha = \frac{b^Tu_k - x_k^TAu_k}{u_k^TAu_k} = \frac{-r_k^Tu_k}{u_k^TAu_k} α=ukTAukbTuk−xkTAuk=ukTAuk−rkTuk
由于 u k = − r k + β k u k − 1 u_k = -r_{k} + \beta_k u_{k-1} uk=−rk+βkuk−1
α = − r k T ( − r k + β u k − 1 ) u k T A u k \alpha = \frac{-r_k^T(-r_k+\beta u_{k-1})}{u_k^TA u_k} α=ukTAuk−rkT(−rk+βuk−1)
由于 r k T u k − 1 = 0 r_k^Tu_{k-1}=0 rkTuk−1=0
有
α k = r k T r k u k T A u k \alpha_k = \frac{r_k^Tr_k}{u_k^TA u_k} αk=ukTAukrkTrk
由于 α k A p k = r k + 1 − r k \alpha_kAp_k = r_{k+1}-r_k αkApk=rk+1−rk
继续代入有
β k + 1 = r k + 1 T r k + 1 r k T r k \beta_{k+1} = \frac{r_{k+1}^Tr_{k+1}}{r_{k}^Tr_{k}} βk+1=rkTrkrk+1Trk+1
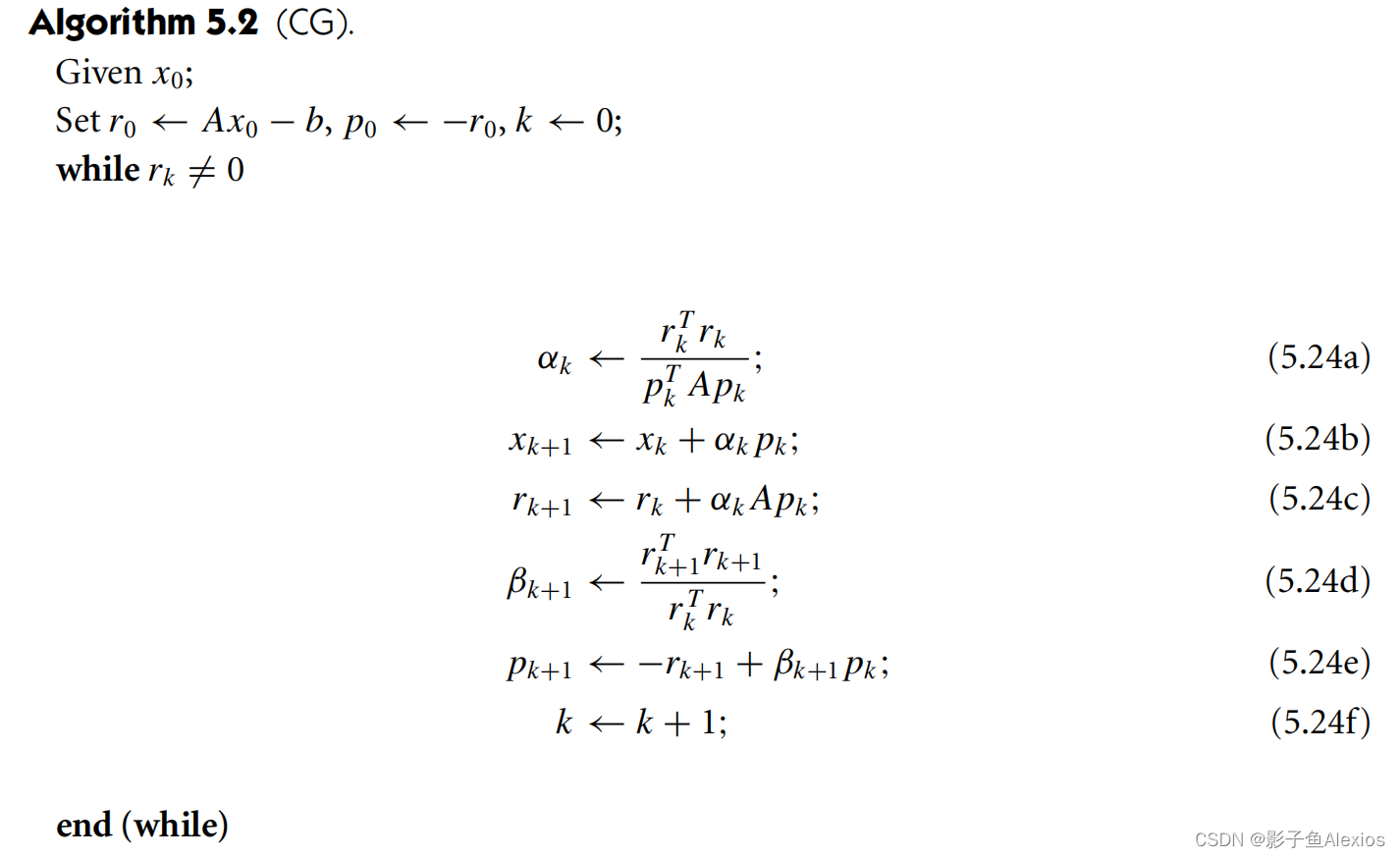
下一节中,将介绍牛顿共轭梯度法