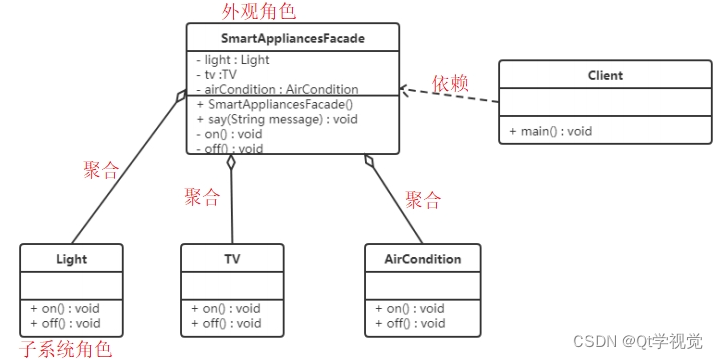
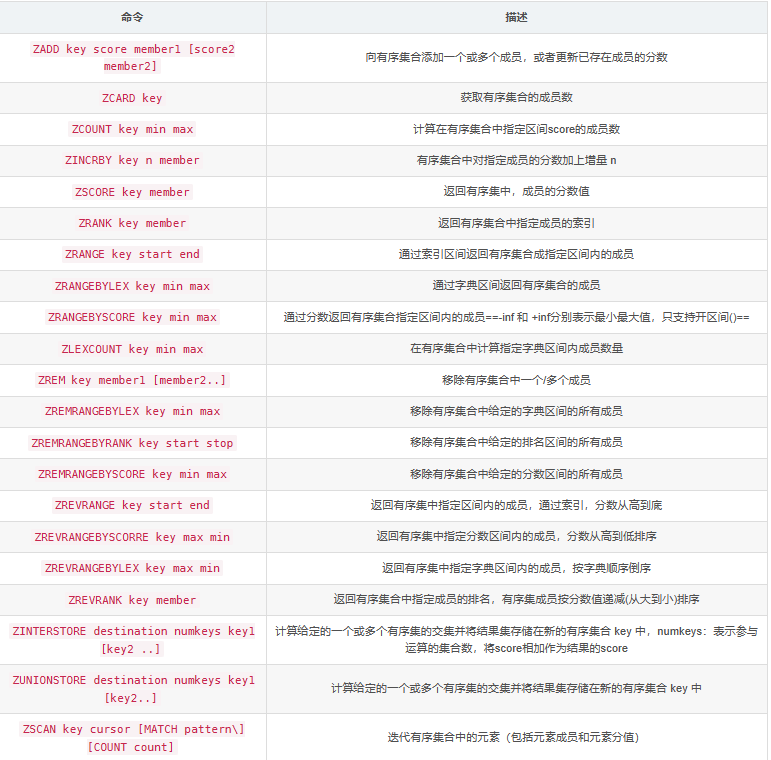
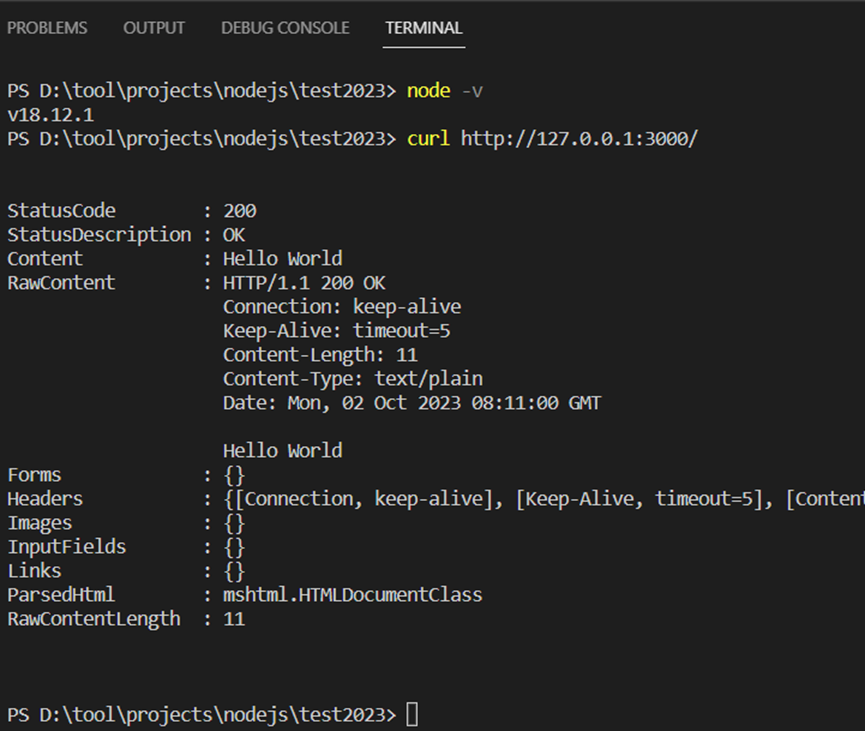
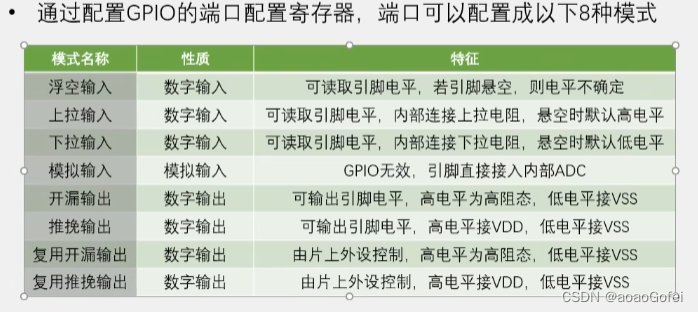
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,下半部分介绍带约束的优化,中间会穿插一些路径规划方面的应用实例
三十二、函数的光滑化技巧
1、Inf convolution 卷积操作
Inf convolution 卷积操作适应于凸函数,Inf convolution 卷积操作的目标是把不光滑的凸函数进行光滑近似,并使得光滑近似后的函数于原函数尽量吻合
对于两个凸函数 f 1 f_1 f1、 f 2 f_2 f2,它们之间的Inf convolution 卷积操作记为 f 1 □ f 2 f_{1}□ f_{2} f1□f2,即找一个 u 1 u_1 u1和 u 2 u_2 u2,满足 u 1 u_1 u1+ u 2 u_2 u2= x x x的条件下,使得 f 1 ( u 1 ) + f 2 ( u 2 ) f_{1}(u_{1})+f_{2}(u_{2}) f1(u1)+f2(u2)最大或最小,如下面的第一个表达式所示,由于满足 u 1 u_1 u1+ u 2 u_2 u2= x x x,因此可消去一个u进行简化,简化后的表达式如下面第二个式子所示:
( f 1 □ f 2 ) ( x ) = inf ( u 1 , u 2 ) ∈ R d × R d { f 1 ( u 1 ) + f 2 ( u 2 ) : u 1 + u 2 = x } ( f 1 □ f 2 ) ( x ) = inf u ∈ R d { f 1 ( u ) + f 2 ( x − u ) } \begin{aligned}(f_1□ f_2)(x)&=\inf_{(u_1,u_2)\in\mathbb{R}^d\times\mathbb{R}^d}\{f_1(u_1)+f_2(u_2):u_1+u_2=x\}\\(f_1□ f_2)(x)&=\inf_{u\in\mathbb{R}^d}\{f_1(u)+f_2(x-u)\}\end{aligned} (f1□f2)(x)(f1□f2)(x)=(u1,u2)∈Rd×Rdinf{f1(u1)+f2(u2):u1+u2=x}=u∈Rdinf{f1(u)+f2(x−u)}
Inf convolution 卷积具有对称性,即 f 1 □ f 2 = f 2 □ f 1 f_1□ f_2=f_2□ f_1 f1□f2=f2□f1
Inf convolution 卷积的几何解释如下图所示,假设我们考虑两个凸函数,一个是常见的绝对值函数 f ( x ) = ∣ x ∣ \color{red}{f(x)=|x|} f(x)=∣x∣,另一个是二次函数 g ( x ) = 1 2 x 2 g(x)=\frac12x^2 g(x)=21x2,如下面的第一幅图所示,对这两个函数进行Inf convolution 卷积操作,即将光滑的函数 g ( x ) = 1 2 x 2 g(x)=\frac12x^2 g(x)=21x2的原点不断地在绝对值函数 f ( x ) = ∣ x ∣ \color{red}{f(x)=|x|} f(x)=∣x∣上进行移动,依次得到下面的第二幅图和第三幅图,最终得到包络即f函数与g函数的Inf convolution 卷积操作。

如果min可以取到的话, e p i ( f □ g ) = e p i ( f ) + e p i ( g ) epi(f□g)=epi(f)+epi(g) epi(f□g)=epi(f)+epi(g)
Inf convolution 卷积操作的原理其实就是拿光滑凸函数的轮廓去把不光滑的地方利用包络给它磨圆
2、Moreau 包络
Moreau envelope是Inf convolution 卷积操作的一个特例,即将被卷积函数更改为一个二次函数或者说范数的平方,如下式所示:
γ f : = f □ ( 1 2 γ ∥ ⋅ ∥ 2 ) ^\gamma f:=f\Box\left(\frac{1}{2\gamma}\|\cdot\|^2\right) γf:=f□(2γ1∥⋅∥2)
其具体表达式如下式所示:
γ f ( x ) : = inf u ∈ R d { f ( u ) + 1 2 γ ∥ x − u ∥ 2 } ^\gamma f(x):=\inf_{u\in\mathbb{R}^d}\{f(u)+\frac{1}{2\gamma}\left\|x-u\right\|^2\} γf(x):=u∈Rdinf{f(u)+2γ1∥x−u∥2}
当一个函数时封闭的凸函数时,inf一定可以取到最小值, γ \gamma γ具有平滑参数的作用, γ \gamma γ越小,平滑后的函数与原函数越接近。

下面来看一个Pinball函数的示例,Pinball函数的定义如下
ℓ s 1 , s 2 ( x ) = { s 1 x if x ≤ 0 s 2 x if x ≥ 0 \ell_{s_1,s_2}(x)=\begin{cases}s_1x&\text{if}x\le0\\s_2x&\text{if}x\ge0\end{cases} ℓs1,s2(x)={s1xs2xifx≤0ifx≥0
其中, s 1 ≤ 0 ≤ s 2 s_1\leq0\leq s_2 s1≤0≤s2,Pinball函数的Moreau 包络函数如下所示
γ f ( x ) = ( f □ g ) ( x ) = = { s 1 x − γ s 1 2 2 , if x < s 1 1 2 γ x 2 , if x ∈ [ γ s 1 , γ s 2 ] s 2 x − γ s 2 2 2 , if x > s 2 \gamma f(x)=(f\Box g)(x)==\quad\begin{cases}s_1x-\gamma\frac{s_1^2}{2},&\text{if }x<s_1\\\frac{1}{2\gamma}x^2,&\text{if }x\in[\gamma s_1,\gamma s_2]\\s_2x-\gamma\frac{s_2^2}{2},&\text{if }x>s_2\end{cases} γf(x)=(f□g)(x)==⎩ ⎨ ⎧s1x−γ2s12,2γ1x2,s2x−γ2s22,if x<s1if x∈[γs1,γs2]if x>s2
一个经典的例子是Huber函数 ℓ − 1 , 1 \ell_{-1,1} ℓ−1,1,即 s 1 s_1 s1取-1, s 2 s_2 s2取1

相关证明如下:

当我们不断地把 γ \gamma γ值减小,平滑后的函数与原函数也更加接近,包络的下边缘也会越来越尖,如下图所示:

Moreau 包络具有一个良好的性质,即一个函数与它的Moreau 包络函数的最小值相同,即
∀ γ > 0 , inf x ( ( γ f ) ( x ) ) = inf x f ( x ) \forall\gamma>0,\quad\inf_x\left((^\gamma f)(x)\right)=\inf_xf(x) ∀γ>0,xinf((γf)(x))=xinff(x)
证明过程如下:
inf x ( ( γ f ) ( x ) ) = inf x inf y { f ( y ) + 1 2 γ ∥ x − y ∥ 2 } = inf y inf x { f ( y ) + 1 2 γ ∥ x − y ∥ 2 } = inf y f ( y ) \begin{aligned} \operatorname*{inf}_{x}\left((^{\gamma}f)(x)\right)& =\inf_x\inf_y\left\{f(y)+\frac1{2\gamma}\left\|x-y\right\|^2\right\} \\ &=\inf_y\inf_x\left\{f(y)+\frac{1}{2\gamma}\left\|x-y\right\|^2\right\} \\ &=\inf_{y}f(y) \end{aligned} xinf((γf)(x))=xinfyinf{f(y)+2γ1∥x−y∥2}=yinfxinf{f(y)+2γ1∥x−y∥2}=yinff(y)

总结一下,用Inf convolution 卷积操作可以对一个不光滑的凸函数进行平滑,平滑后的函数与原函数具有同样的最小值,给一个光滑因子 γ \gamma γ用来调节光滑程度,我们把不光滑的凸函数 f f f的光滑近似记作 ω γ f _{\omega}^{\gamma}f ωγf, ω \omega ω是我们用来光滑 f f f的被卷积的函数, ω \omega ω取 1 2 ∥ ⋅ ∥ 2 \frac{1}{2}\|\cdot\|^2 21∥⋅∥2时,就是Moreau 包络

假设,我们用 g ( x ) = 1 2 x 2 + 1 2 g(x)=\frac12x^2+\frac12 g(x)=21x2+21来作为被卷积的函数,把 g ( x ) g(x) g(x)的原点挪动一遍后,形成的包络如下图所示,我们可以改变 g ( x ) g(x) g(x)来获得不同的效果。

Inf-conv卷积是平滑凸函数的一种常用方法。它可以处理Moreau 包络或者Nesterov 平滑无法处理的问题。

3、Mollifier-Conv
Mollifier卷积是比Inf-conv卷积更一般化的卷积,举一个例子,对于如式所示的函数,它是通过 e − 1 1 − x 2 e^\frac{-1}{1-x^2} e1−x2−1变化而来的,除以其自身的积分相当于进行了缩放操作,这样一个凸起的或者说隆起的函数就称为Mollifier
φ ( x ) = { e − 1 / ( 1 − x 2 ) ∫ − 1 1 e − 1 / ( 1 − s 2 ) d s i f ∣ x ∣ < 1 0 i f ∣ x ∣ ≥ 1 \varphi(x)=\begin{cases}\frac{e^{-1/(1-x^2)}}{\int_{-1}^1e^{-1/(1-s^2)}\mathrm{d}s}&\mathrm{~if~}|x|<1\\0&\mathrm{~if~}|x|\geq1&\end{cases} φ(x)=⎩ ⎨ ⎧∫−11e−1/(1−s2)dse−1/(1−x2)0 if ∣x∣<1 if ∣x∣≥1

更一般的,取 φ ϵ ( x ) : = 1 ϵ φ ( x ϵ ) \varphi_\epsilon(x):=\frac1\epsilon\varphi(\frac x\epsilon) φϵ(x):=ϵ1φ(ϵx),将该函数与下面右图中红色曲线所示的函数进行卷积 f ϵ ( x ) : = ∫ − ∞ + ∞ f ( x + z ) φ ϵ ( z ) d z f_\epsilon(x):=\int_{-\infty}^{+\infty}f(x+z)\varphi_\epsilon(z)dz fϵ(x):=∫−∞+∞f(x+z)φϵ(z)dz,得到了下面右图中的蓝色曲线,其中 ϵ \epsilon ϵ用于调节光滑效果, ϵ \epsilon ϵ越小光滑效果越差,越接近于原函数。

下图中给出了一个二维的例子,在一维的基础上进行了推广
φ ( x ) = { e − 1 / ( 1 − ∥ x ∥ 2 ) ∫ R n e − 1 / ( 1 − ∥ s ∥ 2 ) d s i f ∥ x ∥ < 1 0 i f ∥ x ∥ ≥ 1 \varphi(x)=\begin{cases}\frac{e^{-1/(1-\|x\|^2)}}{\int_{\mathbb{R}^n}e^{-1/(1-\|s\|^2)}\mathrm{d}s}&\mathrm{~if~}\|x\|<1\\0&\mathrm{~if~}\|x\|\geq1&\end{cases} φ(x)=⎩ ⎨ ⎧∫Rne−1/(1−∥s∥2)dse−1/(1−∥x∥2)0 if ∥x∥<1 if ∥x∥≥1

φ ϵ ( x ) : = 1 ϵ n φ ( x ϵ ) f ϵ ( x ) : = ∫ − ∞ + ∞ f ( x + z ) φ ϵ ( z ) d z \begin{gathered}\varphi_\epsilon(x):=\frac1{\epsilon^n}\varphi\Big(\frac x\epsilon\Big)\\\\f_\epsilon(x):=\int_{-\infty}^{+\infty}f(x+z)\varphi_\epsilon(z)dz\end{gathered} φϵ(x):=ϵn1φ(ϵx)fϵ(x):=∫−∞+∞f(x+z)φϵ(z)dz

Mollifier的具体定义如下所示,其满足积分为1,且当 ϵ \epsilon ϵ趋于0的时候, φ ( x ) \varphi(x) φ(x)趋于冲激函数 δ ( x ) \delta(x) δ(x),只要满足这两个条件都可以称为Mollifier
∫ R n φ ( x ) d x = 1 lim ϵ → 0 φ ϵ ( x ) = lim ϵ → 0 ϵ − n φ ( x / ϵ ) = δ ( x ) \begin{aligned}&\int_{\mathbb{R}^n}\varphi(x)\mathrm{d}x=1\\&\lim_{\epsilon\to0}\varphi_\epsilon(x)=\lim_{\epsilon\to0}\epsilon^{-n}\varphi(x/\epsilon)=\delta(x)\end{aligned} ∫Rnφ(x)dx=1ϵ→0limφϵ(x)=ϵ→0limϵ−nφ(x/ϵ)=δ(x)
下面进行简单的推导,为什么使用Mollifier函数进行卷积操作,可对原函数进行平滑处理
d d x f ϵ ( x ) = d d x ∫ f ( x + z ) φ ϵ ( z ) d z = d d x ∫ f ( y ) φ ϵ ( y − x ) d y = ∫ f ( y ) ( d d x φ ϵ ( y − x ) ) d y \begin{aligned} \frac d{dx}f_\epsilon(x)& =\frac d{dx}\int f(x+z)\varphi_\epsilon(z)\mathrm{d}z \\ &=\frac d{dx}\int f(y)\varphi_\epsilon(y-x)dy \\ &=\int f(y)\left(\frac d{dx}\varphi_\epsilon(y-x)\right)dy \end{aligned} dxdfϵ(x)=dxd∫f(x+z)φϵ(z)dz=dxd∫f(y)φϵ(y−x)dy=∫f(y)(dxdφϵ(y−x))dy
即若Mollifier函数是处处连续可微的,则对某个函数进行Mollifier卷积操作后得到的函数也是处处连续可微的,
在下面的例子中,Mollifier函数取为 φ ( x ) = 1 e x + e − x + 2 \varphi(x)=\frac1{e^x+e^{-x}+2} φ(x)=ex+e−x+21,原函数为 f ( x ) = max ( x , 0 ) f(x)=\max(x,0) f(x)=max(x,0),则进行Mollifier卷积后的函数变为下式:
f ϵ ( x ) = ∫ − ∞ + ∞ max ( x + z , 0 ) φ ϵ ( z ) d x = ϵ ln ( 1 + e x / ϵ ) f_\epsilon(x)=\int_{-\infty}^{+\infty}\max(x+z,0)\varphi_\epsilon(z)\mathrm{d}x=\epsilon\ln(1+e^{x/\epsilon}) fϵ(x)=∫−∞+∞max(x+z,0)φϵ(z)dx=ϵln(1+ex/ϵ)
Mollifier卷积后的效果如下面的右图所示:

我们知道 max ( x 1 , x 2 ) \max(x_1,x_2) max(x1,x2)等价于 x 1 + max ( x 2 − x 1 , 0 ) x_1+\max(x_2-x_1,0) x1+max(x2−x1,0),代入上面的表达式,我们可以进一步得到原函数为 max ( x 1 , x 2 ) \max(x_1,x_2) max(x1,x2)时,Mollifier卷积后的结果为 ϵ ln ( e x 1 / ϵ + e x 2 / ϵ ) \epsilon\ln(e^{x_1/\epsilon}+e^{x_2/\epsilon}) ϵln(ex1/ϵ+ex2/ϵ),同理可推广到多个值取max的情况,如下所示:
max ( x 1 , x 2 ) = x 1 + max ( x 2 − x 1 , 0 ) ⟷ x 1 + f ϵ ( x 2 − x 1 ) = ϵ ln ( e x 1 / ϵ + e x 2 / ϵ ) max ( x 1 , … , x n − 1 , x n ) = max ( x n , max ( x 1 , … , x n − 1 ) ) ⟷ ϵ ln ∑ i = 1 n e x i / ϵ l o g ⋅ s u m ⋅ e α p \begin{aligned}\max(x_1,x_2)&=x_1+\max(x_2-x_1,0)\quad\longleftrightarrow\quad&x_1+f_\epsilon(x_2-x_1)=\epsilon\ln(e^{x_1/\epsilon}+e^{x_2/\epsilon})\\\max(x_1,\ldots,x_{n-1},x_n)&=\max(x_n,\max(x_1,\ldots,x_{n-1}))\quad\longleftrightarrow\quad&\epsilon\ln\sum_{i=1}^ne^{x_i/\epsilon\quad\mathsf{log}\cdot\mathsf{sum}\cdot\mathsf{e}\alpha\mathbf{p}}\end{aligned} max(x1,x2)max(x1,…,xn−1,xn)=x1+max(x2−x1,0)⟷=max(xn,max(x1,…,xn−1))⟷x1+fϵ(x2−x1)=ϵln(ex1/ϵ+ex2/ϵ)ϵlni=1∑nexi/ϵlog⋅sum⋅eαp

–
当 ϵ \epsilon ϵ取1时, max { x 1 , … , x k } \max\{x_1,\ldots,x_k\} max{x1,…,xk}函数经过Mollifier卷积处理后的示意图如下所示:

所以, f ( x ) : = log ( ∑ k = 1 n exp x k ) f(x):=\log\left(\sum_{k=1}^n\exp x_k\right) f(x):=log(∑k=1nexpxk)可以被视为光滑的max函数的替代品,在工程中很常用。
若我们将Mollifier函数更改为 φ ( x ) = 2 ( x 2 + 4 ) 3 / 2 \color{red}{\varphi(x)=\frac2{(x^2+4)^{3/2}}} φ(x)=(x2+4)3/22,原函数为 f ( x ) = max ( x , 0 ) f(x)=\max(x,0) f(x)=max(x,0),则进行Mollifier卷积后的函数变为下式,这个函数也被称为CHKS函数,常用作光滑化的max 函数来对max函数进行替代。
f ϵ ( x ) = ∫ − ∞ + ∞ max ( x + z , 0 ) φ ϵ ( z ) d x = x + x 2 + 4 ϵ 2 2 f_\epsilon(x)=\int_{-\infty}^{+\infty}\max(x+z,0)\varphi_\epsilon(z)\mathrm{d}x=\frac{x+\sqrt{x^2+4\epsilon^2}}2 fϵ(x)=∫−∞+∞max(x+z,0)φϵ(z)dx=2x+x2+4ϵ2

下面给出了一个Weierstrass变换的例子,Weierstrass变换是连续版本的高斯模糊,他也可以得到光滑的函数

下面给出了一个采用分段光滑的例子
F μ ( x ) = { 0 i f x ≤ 0 ( μ − x / 2 ) ( x / μ ) 3 i f 0 < x < μ x − μ / 2 i f x ≥ μ F_\mu(x)=\begin{cases}0&\mathrm{~if~}x\leq0\\(\mu-x/2)(x/\mu)^3&\mathrm{~if~}0<x<\mu\\x-\mu/2&\mathrm{~if~}x\geq\mu&\end{cases} Fμ(x)=⎩ ⎨ ⎧0(μ−x/2)(x/μ)3x−μ/2 if x≤0 if 0<x<μ if x≥μ

参考资料:
1、数值最优化方法(高立 编著)
2、机器人中的数值优化