盲超分-双循环对比学习退化网络(蒸馏)
Dual Circle Contrastive Learning-Based Blind Image Super-Resolution
IEEE Transactions on Circuits and Systems for Video Technology
10.1109/TCSVT.2023.3297673
盲图像超分辨率(BISR)旨在从包含未知退化的低分辨率(LR)图像中构建高分辨率(HR)图像,具有重要应用价值,但现有方法存在以下问题:
- 忽视不同图像区域的退化特征差异:在 BISR 任务中,LR 图像的退化包含模糊和噪声,且不同区域的退化表现不同。在复杂纹理区域,像素差异大,模糊使像素趋于相似,表现更明显;噪声易融入纹理,不易察觉。而在简单区域,如平滑背景,噪声更明显。然而,以往基于深度学习的方法在估计退化表示时,仅设计一个网络提取不同类型的退化信息,忽视了这种区域差异,导致无法获得有效的退化表示,限制了模型性能 。
- 缺乏对退化表示和超分辨率结果生成的有效监督:
- 退化表示监督困难:以往方法常采用监督学习训练退化提取网络,以获取尽可能包含 LR 图像退化信息的表示,但实际应用中难以获得真实的退化表示作为监督,限制了该方法的实用性。虽然对比学习可用于解决此问题,但现有应用对其约束较弱,导致获得的退化表示不能准确包含 LR 图像的所有退化信息,影响了基于对比学习的 BISR 方法性能。
- 超分辨率结果监督不足:以往 BISR 方法仅使用像素级损失训练网络,虽能使超分辨率结果在像素层面尽可能接近真实图像,但无法有效去除结果中的退化信息,导致最终合成图像出现伪影 。
- 浅层特征直接融合导致伪影问题:在现有 BISR 方法中,常使用跳跃连接来保留浅层特征中的纹理信息并缓解梯度消失问题,但图像恢复任务与高级视觉任务不同。在 BISR 任务中,浅层特征包含大量退化信息,若直接与包含较少退化信息的深层特征相加,会使融合后的特征含有大量退化信息,从而在最终的超分辨率结果中引入伪影 。
- 传统深度学习方法的局限性:早期基于深度学习的图像超分辨率方法大多针对单一退化场景(如仅空间下采样),在实际应用中效果不佳。非盲图像超分辨率方法虽考虑了多种退化,但需要已知退化表示,不适用于退化未知的实际场景。现有的 BISR 方法在处理复杂退化时,存在对噪声处理不足、模型复杂度过高或对特定数据集依赖过强等问题,难以满足实际需求。

通过退化提取网络、蒸馏感知超分辨率网络、退化网络及对比学习策略,解决盲图像超分辨率(BISR)中退化特征提取不充分、监督不足及伪影问题。
框架包含三大核心子网络(图 1):
- 退化提取网络(DEnet):从 LR 图像的不同纹理区域(简单 / 复杂)提取退化表示,捕捉区域特异性退化特征。
- 蒸馏 - based 退化感知超分辨率网络(DDA-SRnet):利用退化表示生成 HR 图像,通过信息蒸馏模块(IDM)去除浅层特征中的退化信息,保留纹理细节。
- 退化网络(DGnet):模拟退化过程,将 HR 图像或超分辨率结果退化回 LR 域,用于对比学习的监督信号生成。
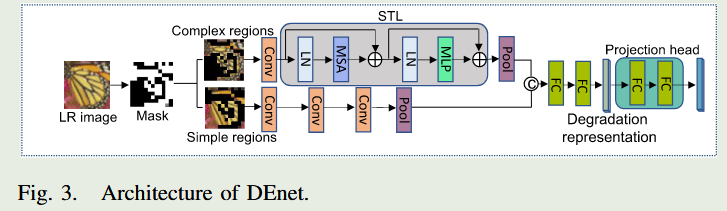

B. Degradation Extraction Network (DEnet)
BISR模型设计中的关键问题之一是如何准确获取图像的退化信息,这将影响模型中采用的后续SR网络的性能。之前的基于深度学习的方法[3]、[4]、[5]、[6]只设计了一个网络来提取不同类型的退化,并使用获得的退化信息来指导SR图像的生成。这些方法忽略了不同退化的特征,从而限制了它们的性能。如前所述,模糊和噪声是BISR任务中常见的退化。从数学上讲,图像的模糊是通过用相邻像素的加权平均值替换原始像素来表示的。在图像的复杂纹理区域中,像素彼此非常不同。这些像素发生了模糊,就像对它们执行类似平均值的操作一样,这使得模糊在复杂区域中看起来更加明显,如图2所示。
同时,噪声的出现通常是通过向每个单个像素添加随机干扰来表示的。因此,噪声很容易在复杂区域中合并,这使得它在该区域中不那么明显。相比之下,它在简单的区域更为明显,例如图像的平滑背景,如图2所示。基于上述分析,我们提出了一种有效的退化提取网络,即DEnet,通过将图像划分为简单和复杂区域来获得图像的退化表示。具体来说,我们提出的DEnet利用两个分支为不同类型的区域生成不同的退化表示。

C.基于蒸馏的DASR网络(DDA SRnet)
在之前的深度BISR方法中,如DASR[4],跳过连接经常被用于高级视觉任务[52]、[53]、[54]。采用跳过连接有两个好处。首先,它可以保留浅层特征中的纹理信息,这有利于构建高质量的SR结果。其次,它可以缓解梯度消失问题,并使网络训练快速收敛。
然而,图像恢复任务(如图像SR)与高级视觉任务有很大不同。在恢复任务中,浅层特征包含大量退化信息,如果将其直接添加到包含较少退化的深层特征中,则生成的特征将包含大量退化,这将在SR结果中引起伪影。为了解决这个问题,我们提出了一种基于蒸馏的DASR网络,即DDA SRnet,其中采用了一个信息蒸馏(ID)模块来提取浅层特征。通过这种蒸馏,我们可以在浅层特征中保留重要的纹理信息,以提高SR结果的质量。ID模块旨在提取空间域和通道域中的特征,如图4所示。在空间域中,卷积块注意力模块[55]中的空间注意力机制用于获得空间注意力图。在信道域中,通过将劣化信息与信道信息聚合来生成信道关注图。分别使用空间注意力图和通道注意力图提取特征。



D.退化网络(DGnet)
我们提出的DGnet旨在将退化表示应用于给定图像,以获得退化图像。根据方程式(1),我们构建了由下采样操作、模糊操作模块和噪声操作模块组成的DGnet,如图7所示。更具体地说,采用双三次下采样将图像从HR转换为LR。模糊操作模块由两个DA块组成,用于从输入退化表示中恢复模糊信息,并将模糊添加到输入图像的特征中。噪声操作模块由两个完全连接的层组成,它可以从退化表示中恢复噪声信息,并将噪声添加到输入图像的特征中。
E 双循环对比学习(DCCL):双向约束优化
在之前的模型[3]、[5]、[6]中,退化表示用于指导BISR的实现。理想的退化表示应尽可能包含LR图像的退化。之前的BISR方法设计了基于监督学习的深度网络来生成退化表示。然而,训练网络需要真实的退化表示作为基本事实,但在实际应用中并不可用。由于采用了无监督学习策略,对比学习可以应用于解决这个问题[4]。训练基于对比学习的模型不需要基础事实,使其更适用于实际应用。然而,对比学习在获得退化表示中的应用受到弱约束,这使得获得的退化表示并不完全包含LR图像的所有退化信息。因此,这限制了基于对比学习的BISR模型的性能。
此外,之前的BISR方法[3]、[4]、[5]、[6]只是采用像素级损失来训练设计的深度网络。采用这种损耗保证了SR结果尽可能接近像素级的地面真实值。然而,仅采用像素级损失并不能有效地消除SR结果的劣化。SR图像中退化的存在将引入伪影并限制模型性能。因此,使SR结果在退化水平上接近地面真实值也是必要的。
为了解决上述问题,我们提出了一种新的学习策略,即DCCL,以实现对退化表示和最终SR结果生成的有效约束。在DCCL中,通过应用得到的劣化表示来引导SR到LR过程,从而获得劣化的LR图像,从而限制劣化表示的生成。将该过程与LR到SR的实现相结合,我们构建了LR-SR-LR学习圈。同时,我们在这个圈子里介绍了两个分支。在第一个分支中,我们强制退化的LR图像和输入的LR图像足够相似,以便退化表示可以尽可能多地包含LR图像的退化。在第二个分支中,我们使SR结果的退化图像接近HR图像的退化图像,以确保SR图像尽可能少地包含退化。
一、退化模型的多因素定义(公式与描述)

这一公式明确表明,真实退化是 模糊、下采样、噪声三者的联合作用,而非单一因素。


实验:
各向异性高斯核和噪声的退化:在第二种情况下,当应用EDSR[12]和RCAN[14]合成HR图像时,我们仍然使用DnCNN[58]首先从LR图像中去除噪声。同时,我们用给定的各向异性高斯核和噪声对IKC[3]进行再训练。请注意,DCLS[5]是针对大小为31×31的模糊核对×4 SR进行训练的,但我们的方法和其他方法通常针对大小为21×21的模糊核进行训练,以用于×4 SR场景。为了与DCLS进行公平的比较,我们还使用大小为31?1的模糊核训练我们的模型。同时,BSRDM[41]的模糊核的生成和我们的方法也不同。我们用BSRDM[41]生成的模糊核重新训练了我们的模型,以实现公平的比较。此外,我们采用了如图9所示的九种典型内核,并在实验中采用了如DASR[4]所示的三级噪声。

