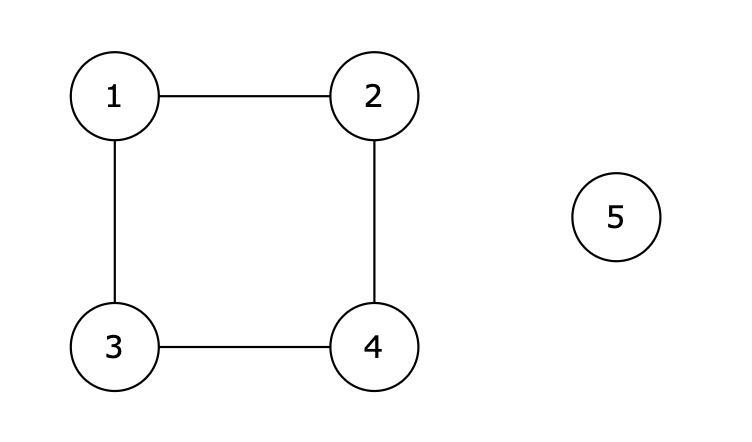
给定一个线性表 L = ( a 1 , a 2 , a 3 , … , a n − 2 , a n − 1 , a n ) L = (a_1, a_2, a_3, \dots, a_{n-2}, a_{n-1}, a_n) L=(a1,a2,a3,…,an−2,an−1,an),它采用带头结点的单链表存储。设计一个空间复杂度为 O ( 1 ) O(1) O(1) 且时间尽可能高效的算法,重新排列链表中的节点,得到新的线性表 L ′ = ( a 1 , a n , a 2 , a n − 1 , … ) L' = (a_1, a_n, a_2, a_{n-1}, \dots) L′=(a1,an,a2,an−1,…)。
要求:
- 给出算法的基本设计思想。
- 根据设计思想,采用 C 或 C++ 语言描述算法,并在关键部分给出注释。
- 说明设计的算法的时间复杂度和空间复杂度。
本文需要用到快慢指针与时空复杂度的知识点,若您不清楚,可参考以下文章:
- 【数据结构】快慢指针探秘:理解链表与数组中的环结构
- 【数据结构】时间复杂度和空间复杂度是什么?
设计思想
该问题的核心是重新排列单链表,使得其从前往后依次为:第一个元素、最后一个元素、第二个元素、倒数第二个元素,依此类推。为了满足题目对空间复杂度 O(1) 的要求,我们不能使用额外的数据结构(如栈或数组),只能通过指针操作来完成。
解题步骤:
- 找到链表的中间节点:使用快慢指针找到链表的中点位置。
- 反转后半部分链表:从中点位置开始,反转链表的后半部分,使得最后一个节点变为新的起始节点。
- 合并前后两部分链表:按照题目要求,将反转后的链表节点依次插入到前半部分链表中,得到重新排列后的链表。
算法实现(C++代码)
以下是该算法的实现代码,代码中包含了详细注释。特别是最后的 while 循环部分,进行了交替合并操作:
#include "bits/stdc++.h"
using namespace std;struct Node {int value;Node* next;
};// 反转链表函数
Node* reverseNode(Node* node) {Node* cur = nullptr, *newNode = nullptr;while (node) {newNode = node;node = node->next;newNode->next = cur;cur = newNode;}return cur;
}Node* rearrangeList(Node* head) {if (!head || !head->next || !head->next->next) return head;// 使用快慢指针找到链表的中间节点Node* slow = head;Node* fast = head;while (fast && fast->next && fast->next->next) {slow = slow->next;fast = fast->next->next;}// 将链表后半部分反转Node* reversedHalf = reverseNode(slow->next);slow->next = nullptr; // 将前半部分和后半部分断开// 合并链表的两部分Node* result = head;while (reversedHalf) {Node* up = result; // 前半部分当前节点Node* down = reversedHalf; // 后半部分当前节点reversedHalf = reversedHalf->next; // 更新后半部分节点指针// 将后半部分的节点插入到前半部分的当前位置之后down->next = up->next;up->next = down;result = down->next; // 移动到下一个位置}return head;
}
代码讲解
-
找到链表的中间节点:快慢指针
fast和slow用于定位链表的中间位置。每次fast移动两步,slow移动一步,当fast到达链表末尾时,slow刚好到达中间位置。这样找中间节点的时间复杂度为 O(n/2) ≈ O(n)。 -
反转链表的后半部分:
reverseNode函数用于将链表的后半部分反转。它通过三指针法:node、cur和newNode实现链表反转,使得最后一个节点成为新的起始节点。 -
合并链表:
while循环执行链表合并操作。合并过程中,我们交替地将前半部分和反转后的后半部分节点串联起来,形成要求的排列顺序。特别说明
while循环up是当前前半部分的节点,而down是当前反转后链表的节点。- 我们将
down节点插入到up后面,并调整指针使得链表按照所需顺序排列。 - 为了保证链表结构不被破坏,我们先将
reversedHalf更新为下一个节点,以防在操作down->next时丢失链表的后续节点。
与其他实现方式的比较
- 递归实现:可以通过递归反向合并链表的前半部分和后半部分,但递归会带来 O(n) 的额外栈空间,不满足 O(1) 的空间复杂度要求。
- 使用栈或数组:虽然可以用栈或数组存储链表元素位置并重新排列,但也会增加 O(n) 的空间复杂度。
- 原地操作:我们当前的实现方式通过反转链表和指针操作完成,达到了 O(1) 的空间复杂度要求,是最优解法。
时间和空间复杂度分析
-
时间复杂度:
- 找中间节点的操作复杂度为 O(n)。
- 反转链表后半部分的复杂度为 O(n/2) ≈ O(n)。
- 合并链表的复杂度为 O(n)。
- 总体时间复杂度为 O(n)。
-
空间复杂度:
- 该算法仅使用几个指针变量,空间复杂度为 O(1),不需要额外的空间存储。
总结
该算法通过使用快慢指针找到链表的中点位置,再反转后半部分链表,并依次将节点合并至前半部分,从而实现了题目所要求的重排。此方法不仅保证了 O(n) 的时间复杂度,也达到了 O(1) 的空间复杂度。
这种解法在面试和考试中是一个常见的考点,理解这个方法将帮助你在遇到类似链表问题时迅速找到高效的解决方案。