在思考一些C语言编程题的解法时我们经常会碰到的一种算法是递归,递归的字面意思是传递回归,会用例子来解释和运用。
递归
例:在控制台输出指定项数的斐波那契数
斐波那契数列数列是指:1,1,2,3,5,8,13,21,34......从第三项开始等于前面两项之和。
思路:递归——这里的“递”(传递)是通过前面两个数值的运算可以得到要求的结果,而“归”(回归)就是任意一个数值的结果必须依赖所有前面的结果进行运算之后才能进行。
传递:A1+A2=A3、A2+A3=A4、A3+A4=A5......
回归:A5=A3+A4、A4=A2+A3、A3=A1+A2......程序
#include<stdio.h>
int Fib(int n)//函数定义
{if (n<3)return 1;elsereturn Fib(n - 1) + Fib(n - 2);
}
int main()
{int n;scanf_s("%d", &n);//项数printf("%d\n", Fib(n));return 0;
}
这里我们还要介绍一下当出现问题时一步一步进行调试。第一步是按下F11(或者热键冲突的就按Fn+F11),第二步按照下面的步骤进行操作就会出现一个监视窗口,然后在窗口中输入变量就可以监视变量的变化,一步一步调试的快捷键跟第一步一致,如果想要逐过程(比如函数)调试就换成F10
![]()

监视窗口:
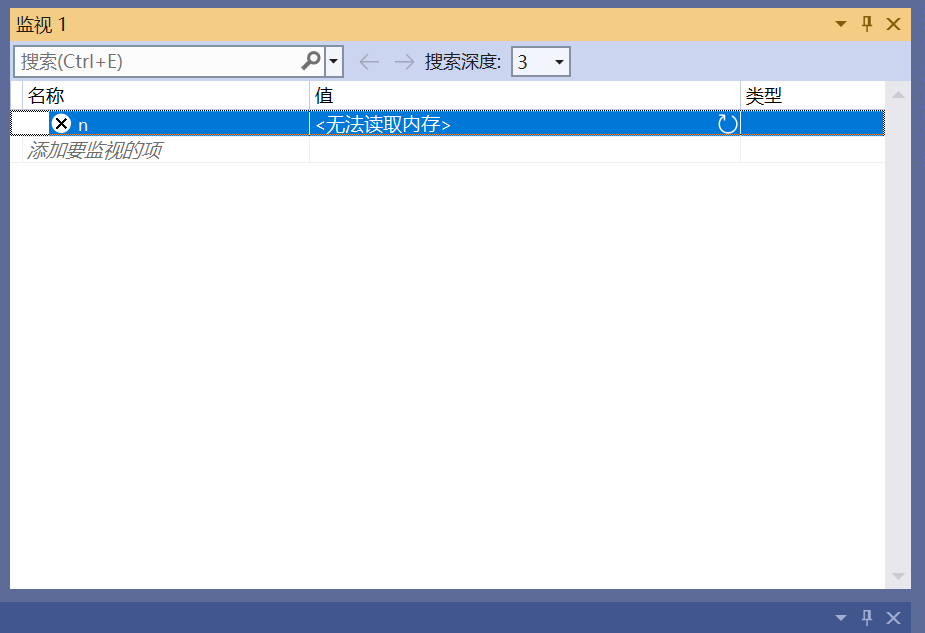
当n=3时,按照从左到右会先回去算n=2,此时还是进入这个函数;不过此时n=2,输出结果为1,然后在重新回到刚刚计算n=3的时候;然后再算n=1的时候。封装成函数可以进行“规律”的复用,提高计算效率,这也是函数强大的作用之一,但是会出现一些问题......
函数堆栈
用求解F(5)的过程来举例,需要理解一个新的概念叫函数堆栈,一种指存储函数调用的顺序还有局部变量信息(包括地址、值、作用域、生命周期)的线性数据结构,遵循后进先出(LIFO)的原则。
函数堆栈工作原理:
①入栈(push):当函数进行调用时,上面所述的信息会被压入堆栈中
②出栈(pop):当函数调用结束了,相关信息会被释放,后调用的函数信息会被先弹出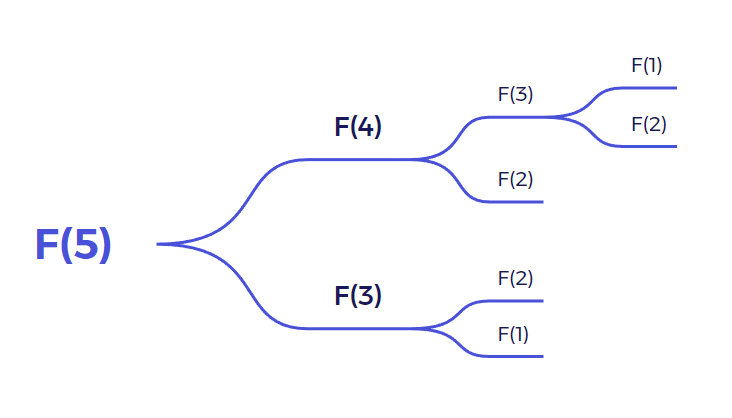
递归中的函数调用是每一次调用都会建立一个新的堆栈直到递归结束所有的信息才被弹出,所以如果堆栈本身的空间如果不够的话很容易造成Stack Overflow即堆栈溢出。比如上图F(3)、F(1)被调用了两次,F(2)则是三次,进行的是无意义的重复。针对此类问题我们之后介绍非递归写斐波那契数列来优化一下。
调用堆栈可以按照下面步骤操作进行查看,搭配逐步调试(F11)来使用。
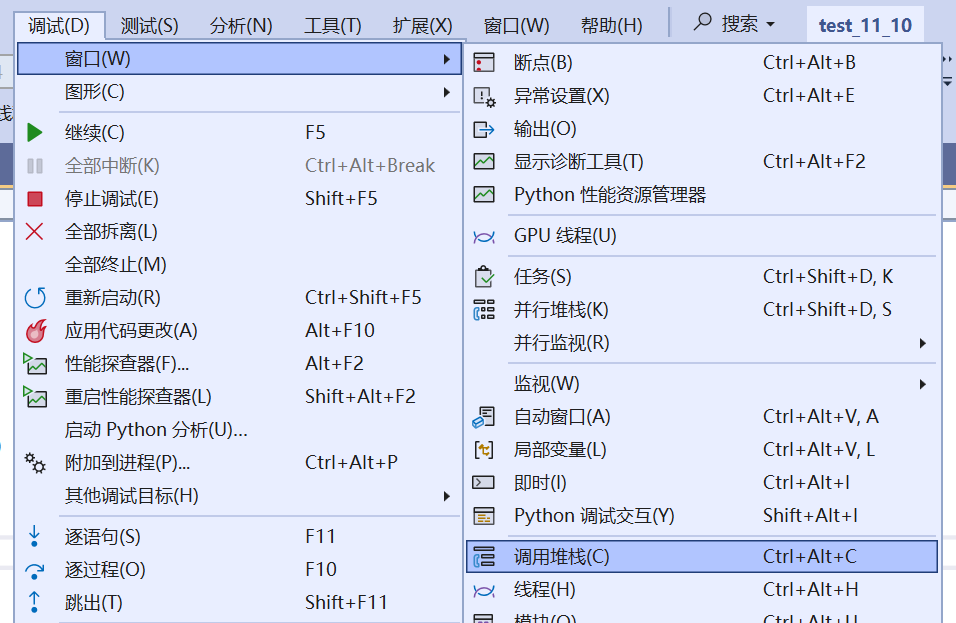
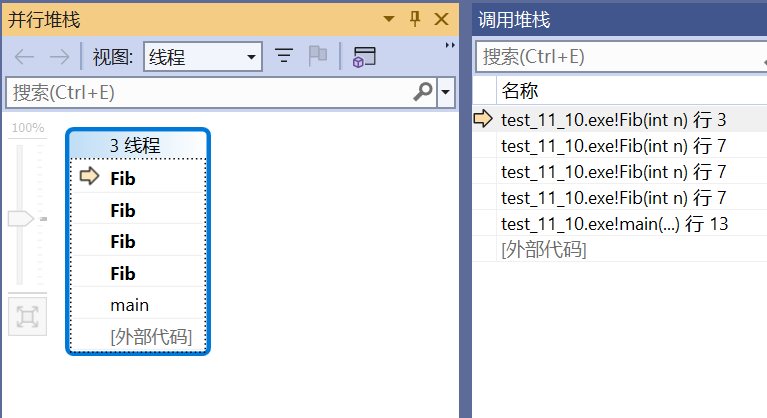
局部变量和全局变量
局部变量指在函数当中创建,在函数进行调用时“出生”,在函数结束调用时“死亡”,这一段也叫做作用域,生命周期。在循环当中的表达式进行定义的也是如此,当离开循环结构便被销毁不能再使用。
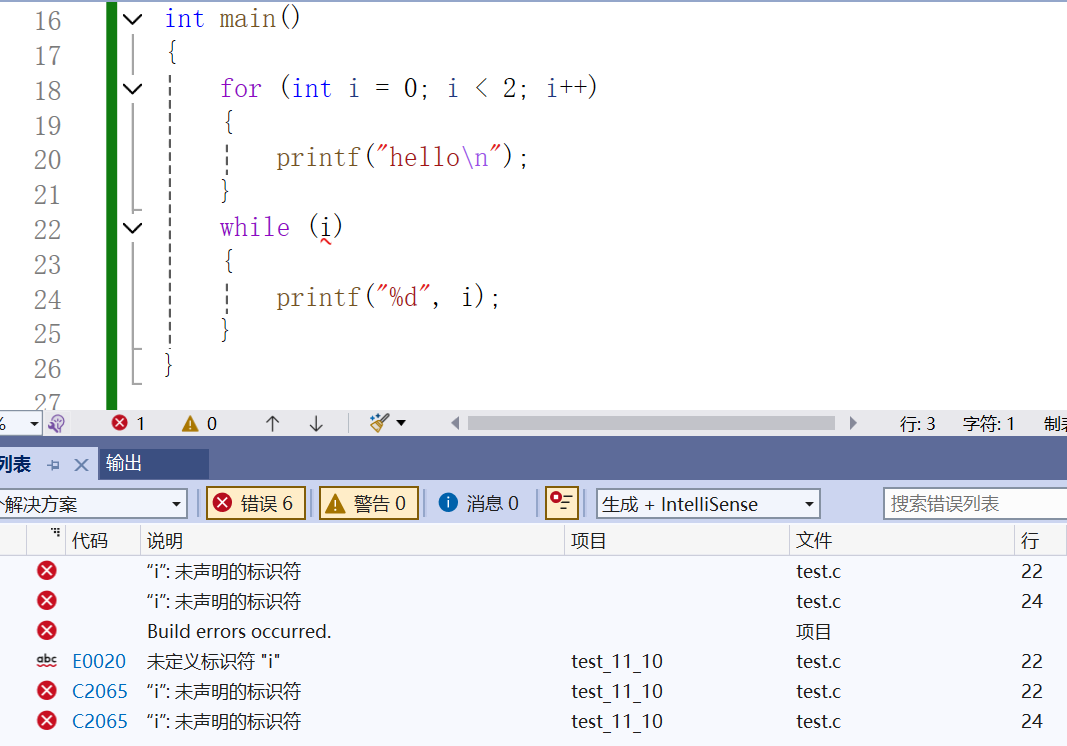
与局部变量相对的是全局变量,让上面的i改成全局变量就不存在“未声明”的问题了。全局变量的生命周期、作用域是一整个程序,在定义处开始“出生”,在程序结束的时候“死亡”,任何函数都可以调用该全局变量。
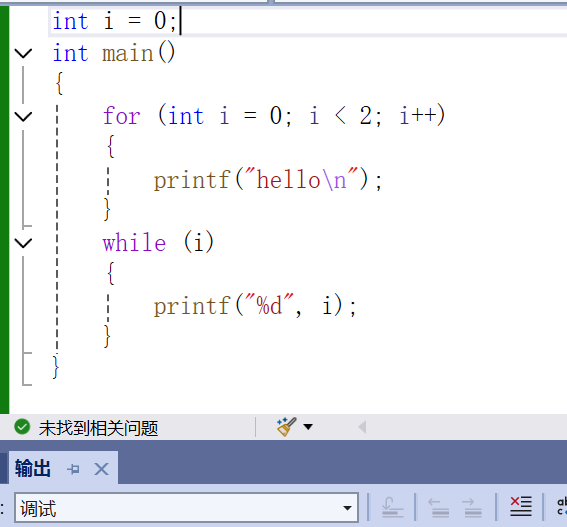
特别地,当全局变量不进行显性初始化时会进行自动赋值为0。参考下面的代码片段。
int i ;
int main()
{printf("i=%d\n", i);for (int i = 0; i < 2; i++){printf("hello\n");}return 0;
}