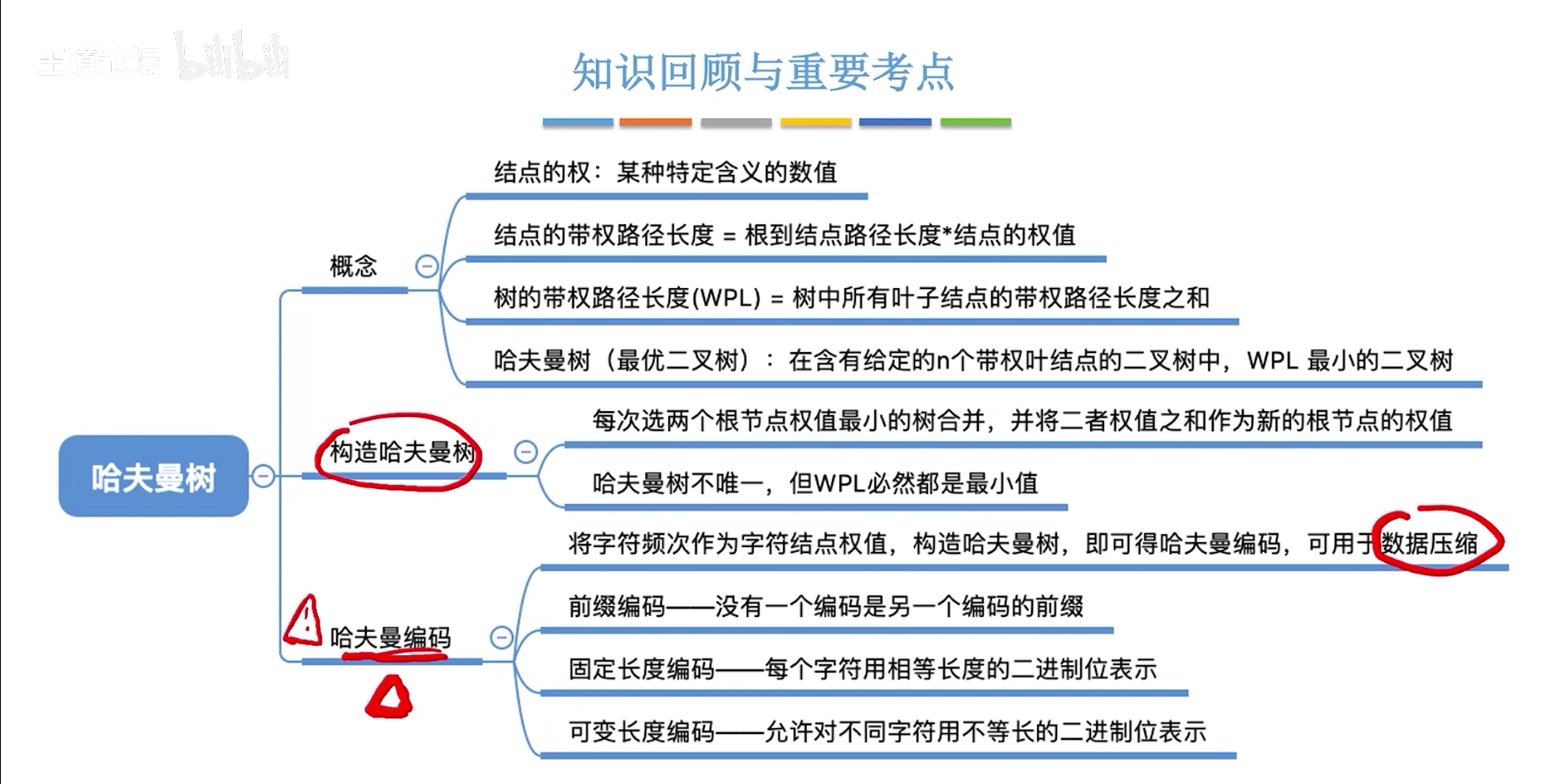
二叉树的内部结构

二叉查找树

二叉查找树，又称二叉排序树或者二叉搜索树

特点:

• 每一个节点上最多有两个子节点
• 任意节点左子树上的值都小于当前节点
• 任意节点右子树上的值都大于当前节点

二叉查找树添加节点 规则:

• 小的存左边
• 大的存右边
• 一样的不存

二叉树的遍历方式

• 前序遍历
  从根结点开始，然后按照当前结点，左子结点，右子结点的顺序遍历
• 中序遍历
  从最左边的子节点开始，然后按照左子结点，当前结点，右子结点的顺序遍历
• 后序遍历
  从最左边的子节点开始，然后按照左子结点，右子结点，当前结点的顺序遍历
• 层序遍历
  从根节点开始一层一层的遍历

二叉树的遍历弊端

平衡二叉树

规则:任意节点左右子树高度差不超过1

平衡二叉树的旋转机制

规则1:左旋
规则2:右旋
触发时机:当添加一个节点之后，该树不再是一颗平衡二叉树

判断是左旋还是右旋

左旋

1. 确定支点:从添加的节点开始，不断的往父节点找不平衡的节点
2. 把支点左旋降级，变成左子节点
3. 晋升原来的右子节点

右旋

1. 以不平衡的点作为支点
2. 把支点右旋降级，变成右子节点
3. 晋升原来的左子节点

数据结构(平衡二叉树)需要旋转的四种情况

• 左左:当根节点左子树的左子树有节点插入，导致二叉树不平衡
• 左右:当根节点左子树的右子树有节点插入，导致二叉树不平衡
• 右右:当根节点右子树的右子树有节点插入，导致二叉树不平衡
• 右左:当根节点右子树的左子树有节点插入，导致二叉树不平衡