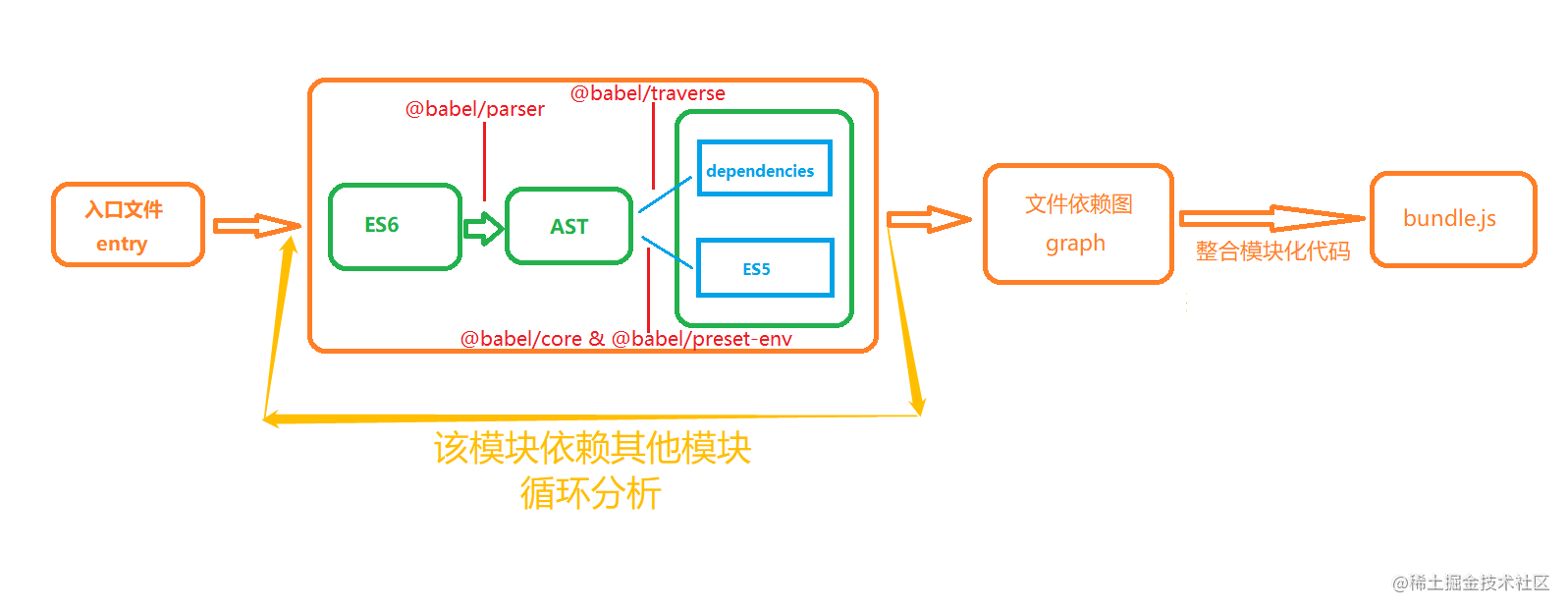
最后一个问题，欧拉公式，

到底要说明的是什么。从欧拉函数的四个特殊值可以看出，

可见这个函数的作用是将角度映射回它原来的数值。在螺旋楼梯的例子中，我们用虚数单位的倍数搭建楼梯，并构造角度，角度是一系列先前角度微分的累积。现在我们将这个角度也就是角度微分的累积，还原为对应的虚数单位的倍数。我们知道，

具体观察，，

解析这个方程，其中

也就是，

是把以虚数单位为半径，四分之一圆周的弧的长度当成周期，取倒数，也就是获得这个周期对应的最小单位（如果为虚数单位，最小单位为），然后把这个单位乘以，也就是当前的阶梯序号即当前阶梯的虚数单位重复的次数，然后整体求倒数，就得到当前垂直圆面的长度单位，而这个单位仍然是相对单位，需要基于所有的先前单位的比例关系才能获得实际的长度，一直到单位1为止。而这个比例关系的总体效果，就是，

所以，从第一个单位1开始累积，此后是那些和半径为虚数单位的四分之一圆周有关的弧长微分的累积，最终构成了四分之一圆周的“高度”，也就是虚数单位。总结来说，如果先前求，求的是从到的过程中，阶梯的圆型底面的四分之一圆周的弧长；那么关于自然对数的次幂，求的就是到过程中阶梯垂直圆型底面的高。

正如先前我们用，

表达任意角度，我们也可以用

来求任意角度对应的“高度”。所以这个高度就可以写成，

由于这个高度包含虚数单位的奇数和偶数次项，那么也就自然出现含有虚数单位和不含虚数单位的两种情况，而这两者，就分别用正弦和余弦表示了。

其实这时候，才真正创造了实轴和虚轴上的有效度量。也就是说，先有了虚数单位的累积，然后根据虚数单位的4次幂周期，构成了复平面；然后，虚数单位半径的等差数列，构成了实轴（正半轴）到虚轴（正半轴）的角的度量，以角度为基础，又构造了从实轴（正半轴）到虚轴（正半轴）的高度的度量，而高度度量可以分解为虚数单位的奇数次和偶数次，而奇数次和偶数次又可以映射回到四个半轴，这又构成了四个半轴的长度的内化刻度的度量。也就是说，

里面的和，说的根本不是复平面上的事，而是垂直于和轴的轴上的高度。高度的涉及虚数单位的部分放在了轴，不涉及虚数单位的部分放在了轴。这样的话，高度和不涉及虚数单位的，以及涉及虚数单位的，就构成了三个维数。这个高度，在先前分析的结构的时候，只是作为楼梯的高度，一个辅助求切线单位z长度的量存在，而并未直接体现在的结构之中，而在中，则以

体现了出来，这里的就对应了

中的，两者的位置互为倒数，是因为它们最终具有相互正交的指向。所代表的向量无论如何都在圆面之中，而代表的则必须垂直于圆面。由于两者垂直，可以认为，如下关系成立，

也就是说，角度对应阶梯的序号。

由此就构成了坐标，

这样一个三维关系。我们知道，

以为半径的螺旋楼梯，转了一圈，从升到，而第二圈会从升到。虽然根据周期性，它呈现出的摆动，但是本质上，高度仍然是幂次的而不是乘数的。也就是说，两个周期的高度不是等距的。若要等距，我们就得把它取对数，这里肯定是自然对数，

由此可见，若我们对取对数，并除以的对数，我们就可以得到在方向上的等距螺线，而且，

这就得到了我们想要的等距螺线，而且我们知道角度对应方向上的4个单位。