量子计算机能解决哪些问题？

经典与量子难度对比在深入示例之前，我们首先讨论一下如何研究和分类各种问题的难度。有些问题可以在经典计算机上轻松解决，我们不需要量子计算机来解决它们。另一方面，有些问题非常困难，需要量子计算机来解决。一个著名的例子是寻找巨大整数的质因数。RSA加密依赖于这个问题的难度，而Shor算法就是为了在量子计算机上解决这个问题而设计的。另一个例子是在未排序的数据集中寻找解决方案——这理论上可以通过被称为Grover算法的量子算法来解决。然而，大多数专家认为，这些类型的算法将需要实现错误校正，而技术尚未成熟。

因此，我们正在寻找的问题是介于非常容易和非常困难之间的甜蜜点——那些当今量子计算机能够处理，但经典计算机却难以处理的问题。

复杂性类别这些问题的难度在计算机科学的一个分支——计算复杂性理论中被分类和分析。在经典计算中有很多不同的复杂性类别，但其中一些最基础的包括：

P：随着问题规模的增加，可以在多项式时间内解决的问题。它们很容易解决。

NP：代表非确定性多项式。这些问题不一定能在多项式时间内解决，但它们的答案可以在多项式时间内验证。

NP完全：NP中最困难的问题，没有已知的多项式解决方案。这就是著名的旅行商问题和数独游戏所在的地方。

BPP：有界误差多项式问题，可以通过概率经典计算机在多项式时间内在一定的误差阈值内解决。

当量子计算的概念被发明时，人们花费了相当大的努力来弄清楚这些新型计算机能够有效解决哪一类问题。因此，一个新的问题类别被发明了：

BQP，或有界误差量子多项式问题。这是BPP的量子等价物：它是由量子计算机在多项式时间内解决的决策问题类别，错误的可能性很小。

用例1：模拟强子动力学

首先，深入研究华盛顿大学马丁·萨维奇（Martin Savage）的团队发表的一篇论文，题为

《Quantum Simulations of Hadron Dynamics in the Schwinger Model Using 112 Qubits》。

如果你不是一个高能物理学家，你可能仍然熟悉“强子”这个词，就像在大型强子对撞机（LHC）中一样，这是一个巨大的粒子加速器，周长27公里，最终有可能观察到希格斯玻色子。强子是一种亚原子复合粒子，由其他称为夸克的小粒子组成。强子的一些例子是中子和质子。简单介绍一下，大型强子对撞机的建造是为了通过超高能量的粒子碰撞来研究基础物理。通过大型强子对撞机，科学家们希望更多地了解早期宇宙和自然的基本规律。原则上，这些粒子的相互作用可以用一台足够强大的量子计算机从头到尾模拟出来。我们还没有完全做到，但我们正在取得进展。Schwinger模型是一种流行的、简单的模型，用于模拟这些动态。这是一个描述电子和正电子通过光子在1+1D（即时间和一个空间维度）中相互作用行为的模型。该模型与量子色动力学（QCD）有很多相似之处，量子色动力学描述了夸克和强子如何相互作用，但QCD极难模拟。因此，Schwinger模型经常被用作一个玩具模型来研究两者共同的一些现象。为了理解他们为什么要解决这个问题，让我们问自己一系列问题。首先，为什么他们有理由相信在量子计算机上模拟这个过程是可行的？在这种情况下，Schwinger模型中的电子和正电子具有筛选效应，导致远处费米子之间的相关性随着分离呈指数衰减。这意味着从芯片一侧的量子比特到另一侧的量子比特之间没有那么多必要的远程相互作用，所以，这对于我们今天可用的硬件来说是很好的。接下来，为什么这个话题会引起人们的兴趣？总的来说，高能物理学引起了人们极大的兴趣。人们愿意花费数十亿美元来建造大型强子对撞机，全球成千上万的科学家和技术人员将他们的职业生涯奉献给了这个领域。虽然Schwinger模型过于简单化，并没有设计成覆盖三个空间维度，但它仍然是整个理论的一个有用的简化。最后，这项工作是如何完成的，或者如果我们希望继续这项工作，我们将如何处理这个问题？

在仿真类型的实验中，VQE是最常见的方法之一，第一步几乎总是相同的：准备基态。在这种情况下，它是真空状态。在这个实验中，他们使用了一个名为SC-ADAPT-VQE的新版本VQE（它代表可扩展电路-自适应衍生装配伪trotter ansatz-VQE）来准备这个真空上的基态和强子波包。下一步是让强子随时间进化。最后，确定您想要测量的可观察对象并测量它们。如果这些步骤听起来有点熟悉，减去强子波包部分，那是因为这些步骤非常类似于我们在上一课中讨论的QAOA示例。我们从一个熟悉的状态开始（这里是真空状态），然后我们让它随着时间的推移，用一系列的指数哈密顿量来演化。许多变分算法都遵循这种一般方法。不过，这里有一个很大的不同，那就是在我们开始让它进化之前，我们在我们的电路中心创造了强子波包。那么，我们如何创建波包呢？在真空中，强子可以通过在相邻位置产生费米子-反费米子对而被激发。通过在不同位置制备这种强子的叠加，可以制备任意波包。作者将他们的波包集中在电路的中间，以观察进化而不触及边界。但请记住：当使用噪声qpu时，比赛的名称是保持电路深度可管理。为此，SC-ADAPT-VQE协议使用长度尺度上的对称性和层次结构来确定用于状态准备的低深度量子电路。这将创建一个参数数量较少的ansatz，因此深度较浅。该实验在IBM Quantum Heron设备上运行，包括几种不同类型的错误缓解和抑制：动态解耦、零噪声外推、泡利旋转和最近开发的一种称为算子退相干重整化的技术。

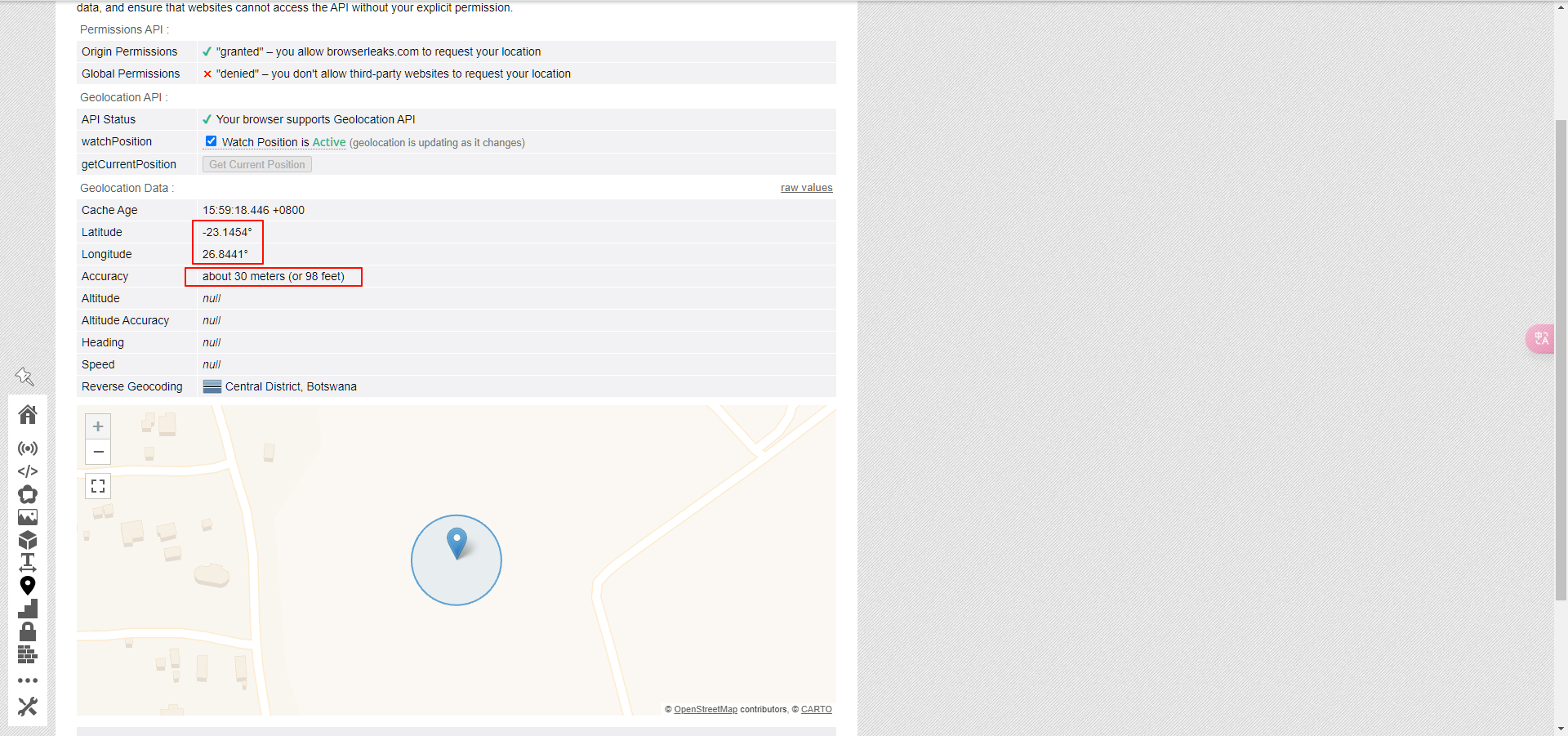
上面这张图显示了我们感兴趣的可观测物，手性凝聚物，它基本上是强子的超流体相。现在，我们可以看到这个波包位于被指定运行这个实验的站点的中心。黑线是经典模拟（计算成本很高）的无错误结果，而带有错误条的点是来自133量子位IBM量子计算机都灵的结果。我们在波包演化中看到两个不同的时间步长。在时间t=1时，可以看到手性凝聚是窄的和局域化的，它也与经典模拟很吻合。在t=14时，分布更加分散。与模拟器的比较现在还不那么完美，但你仍然可以明显地看到理论和数据之间非常好的一致性。总之，这是一个非常酷的模拟工作类型的例子，其目的是更精确地解决困难的理论问题，并利用实验来接受或拒绝理论，以期发现新的物理学，建造改进的探测器，并在最基本的层面上更好地理解自然。

用例2：优化镜像Ising自旋

该例子侧重于优化，并将深入研究一篇名为“偏场数字化反非对称量子优化”的论文，该论文是（https://arxiv.org/abs/2405.13898）由Kipu量子团队和西班牙巴斯克大学的成员完成的。本文提出了一种新的优化方法，并将其应用于寻找伊辛自旋镜像的基态。许多组合优化问题可以重新表述为求解伊辛哈密顿算子的低能态。伊辛模型描述了一系列微观自旋的相互作用。在某些情况下，该模型预测自旋的行为就像玻璃一样，其中磁矩在所谓的“冻结温度”以上是无序的。我们像之前一样，从一系列的定义开始。第一种是反绝热，这是一种抑制系统所经历的非绝热效应的进化，无论这些过程发生得有多快。回想一下上一集的绝热定理——如果你希望系统保持基态，你通常需要非常缓慢地演化一个系统。这是一个大问题，因为我们发展事物的速度越慢，出现错误的时间就越多。反绝热驱动（CD）旨在通过添加抵消这些不需要的激励的项来解决这个问题。这里的主要思想是通过抑制可能导致虚假跃迁的激发来加速整个实验并减少量子电路深度。

现在来看标题中的另一个术语：偏差场。其他迭代算法，如VQE，将经典参数带入状态，并使用经典优化器在多维参数空间中搜索产生固定哈密顿量最小期望值的参数集。在这种情况下，它们每次都改变哈密顿量，从已知情况绝热地移动到感兴趣的情况。为了改变哈密顿量，他们简单地直接应用一次迭代的Pauli-Z期望值作为下一次迭代哈密顿量中的偏差场。通过这种方式，它们将动态导向实际的解决方案，而不需要经典的优化器。那么，为什么这个实验有趣呢？伊辛自旋镜像是物理学的基本兴趣，但这种新方法比这更普遍。它可以应用于许多优化问题，因此具有广泛的研究价值。为什么我们认为这行得通呢？他们提出的算法加速了进化以减少电路深度，同时也抑制了非绝热转换（non-adiabatic transitions）。此外，它不依赖于任何经典的优化子程序，这可能是一个问题，导致贫瘠的高原和卡在局部最小值。最后，作者还确保将问题哈密顿量中的交互与实际qpu中的硬件连通性保持一致，这一点非常重要。那么，这个方法是如何工作的呢？

同样，它不使用任何经典的优化器，不像大多数其他迭代量子算法。相反，通过将每次迭代的解，输入到下一次迭代的输入中，偏场数字化量子优化算法会逐步改进基态，使其越来越接近最终进化状态。结合反非绝缘协议，我们甚至可以用短深度量子电路来做到这一点，它应该在嘈杂的硬件上平稳运行。

因此，在进行实验时，作者选择在布里斯班的127量子位IBM量子计算机上运行该算法。下图显示了在100量子位上随机生成的最近邻自旋玻璃实例的优化算法的第8次迭代。他们比较了DCQO和BF-DCQO的理想经典模拟结果，以及在量子计算机上运行的实验结果。他们还展示了一个名为Gurobi的经典求解器的结果作为参考。与DCQO相比，只需要10次迭代，BF-DCQO就提供了巨大的增强。虽然由于噪声的影响，实验结果与理想结果略有差异，但性能仍优于理想的DCQO。这表明，在量子优化方面仍有许多出色的进展，并且首次在超过100个量子比特上报告了良好的结果。

用例3：mRNA二级结构预测

最后，我们将讨论来自Moderna Pharmaceuticals的一篇论文，名为《mRNA二级结构预测使用实用规模量子计算》

（mRNA Secondary Structure Prediction Using Utility-Scale Quantum Computers.）。首先，简要回顾一下mRNA。信使RNA是一种参与蛋白质合成的RNA。它基本上是读取DNA给出的指令。mRNA的二级结构是链的折叠方式，如下图所示。RNA二级结构预测问题是寻找组成RNA的碱基或核苷酸序列最稳定的折叠问题：腺嘌呤(A)，胞嘧啶(C)，尿嘧啶(U)和鸟嘌呤(G)。下图显示了mRNA中发现的一些常见折叠结构，每种颜色代表不同类型的二级结构。是什么使一个结构比其他结构更有利还没有得到很好的理解；我们所能做的就是计算哪个结构的自由能比展开态的最低。这就是量子计算机的用武之地。

那么，为什么mRNA的二级结构很重要呢？准确预测它们不仅对理解DNA和我们的基因至关重要，而且对设计基于rna的治疗方法（如COVID-19疫苗）也至关重要。由于存在大量可能的配置，这一直被认为是经典计算机的一个令人生畏的优化问题。对于某些构型，已知它是np完全问题。然而，在量子计算机上，我们可以将二级结构预测表述为二进制优化问题——我们知道如何处理。此外，文献中已经有证据表明，在小型量子设备和量子模拟器上可以准确预测RNA。但这在更大的硬件上行得通吗？这个实验是使用一种叫做风险条件值变分量子特征求解器来完成的，它是对传统VQE算法的改进，有望达到更好的收敛性。