-
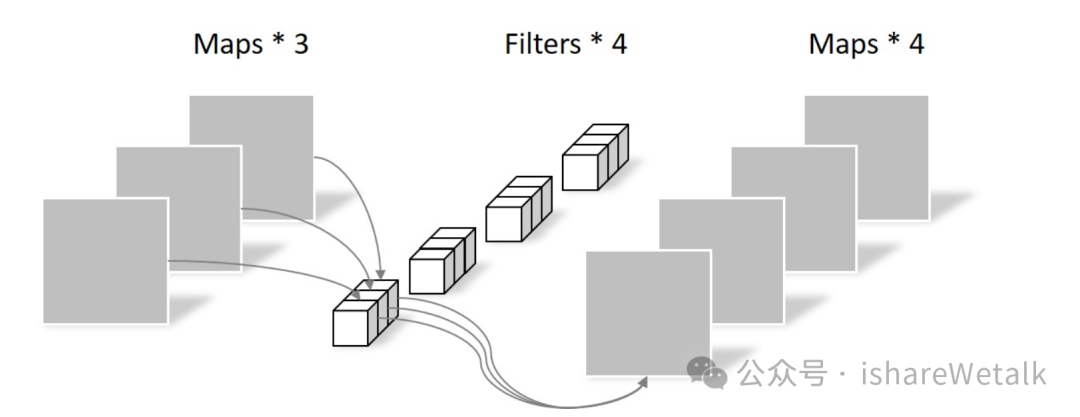
1*1卷积
-
分组卷积&深度可分离卷积
-
空洞卷积、膨胀卷积
-
转置卷积
https://zhuanlan.zhihu.com/p/80041030
https://yinguobing.com/separable-convolution/#fn2
1×1的卷积可以理解为对通道进行加权,对于一个通道来说,每个像素点加权是一样的;而对于一个普通的卷积来说,一个通道上,每个像素点的权重是不一样的;1×1的卷积,对于单个通道上像素点加权是一样的;有几个卷积核就有几个输出特征图;
分组卷积 group convolution;是对输入通道进行分组;输出通道并不是由所有的输入通道共同作用的;会有一种情况,比如输入通道是4,输出通道是2,输出通道的第一个通道只跟输入通道的第1、3个通道有关;输出通道的第二个通道只跟输入通道的第2、4个通道有关;如果输入通道有这样的关系时,我们可以采用分组卷积,设置组数group=2,这时有几个组就会有几个输出通道;这种情况是我们对每个组进行一次卷积,如果我们对每个组进行多次卷积,那么卷积核的个数就会增加了;这样也有一个问题,就是输入特征图的通道之间没有交互,所以这种情况下,在后面的卷积过程中,会有通道之间的随机混合或者用1×1的卷积;poinwise convolution;
深度可分离卷积,是特殊的分组卷积,有几个输入通道,就分成几个组,输入通道之间完全相互独立,deepwise convolution;这种情况下,后面通常会跟着 pointwise convolution;
空洞卷积 或者 膨胀卷积,对应着Conv2d中的,dilation,默认的api设置是1,在参数量不变的情况下,增加了感受野;指的是索引之间相差多少;指的是两次卷积的索引之间 相差的距离就是dilation-1行 或者 列;输出特征图在计算大小的时候,input_h不变,kernel_h=kernel_h + (dilaiton-1)*(kernel_h-1),对应的计算输出特征图的shape;
关于感受野:
- 2个3×3的卷积核 相当于 1个5×5卷积核感受野
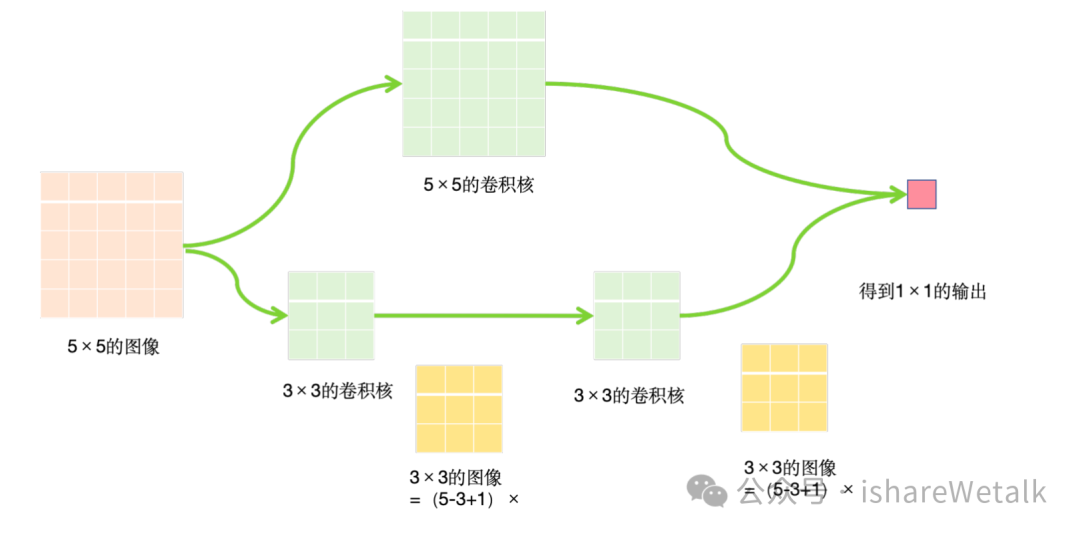
①减少了参数量 ②增加了非线性变换
转置卷积:首先普通卷积的三张理解
-
取出区域,逐元素相乘,然后torch.sum函数
-
把每次取出的input region拉直,形成矩阵
5×5的input feature,3×3的kernel,输出3×3的特征图,对着取到input region有9个,我们把9个region拉直成行向量,9个行向量,与 kernel拉成的列向量 进行矩阵相乘,得到输出的列向量,把输出的列向量,reshape成输出特征图的尺寸,完成卷积
-
对于kernel每次移动的位置,把kernel填充成跟输入特征图一样的大小,把kernel同样拉直,拼接,按行拼接,input拉成列向量,同样的原理,再reshape 得到输出
那什么是转置卷积呢?转置卷积就是把 得到的 kernel阵拼成的行向量 9×25,转置成25×9,再和输出特征图拉成的列向量 9×1 进行相乘,得到25×1的列向量,这样是不是很神奇,如果再reshape一下,不就变成了 输入特征图的尺寸 5×5
这就是转置卷积,上采样,还原尺寸,注意是还原尺寸,而不会还原具体的数值;所谓转置就是因为我们把拉成行向量的kernel阵,进行了转置。
以下是几张图,帮助理解:
普通卷积:
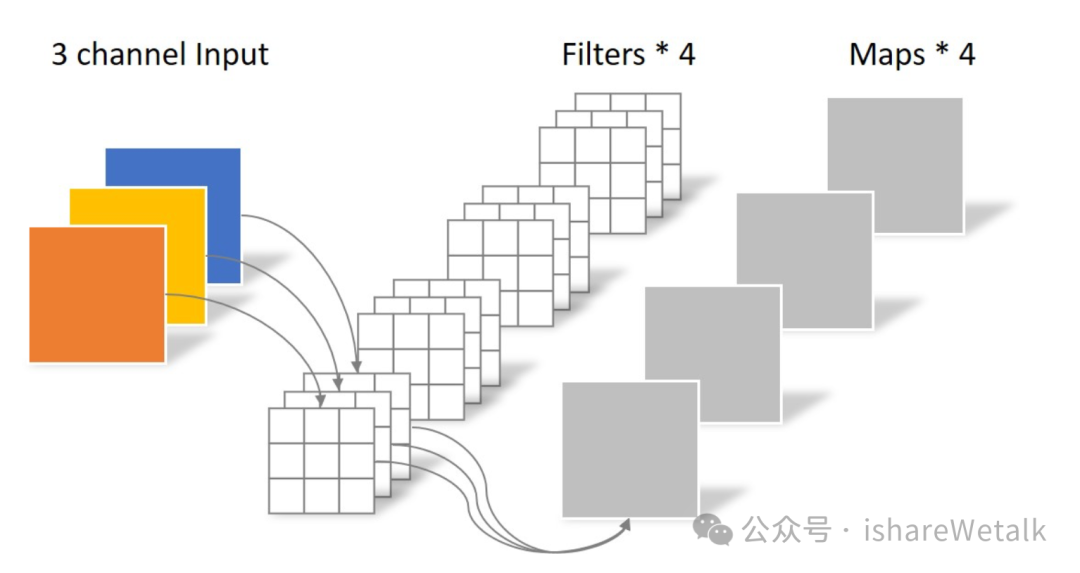
deepwise convolution
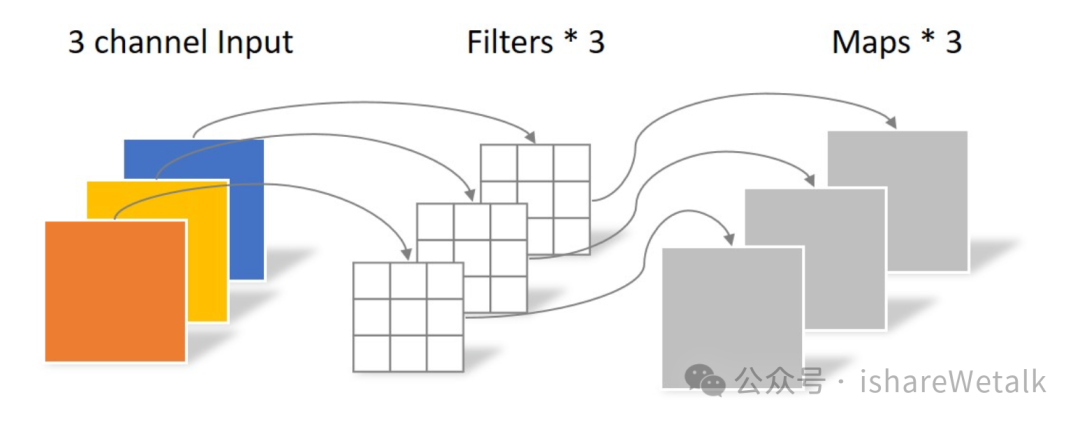
1×1卷积 pointwise convolution