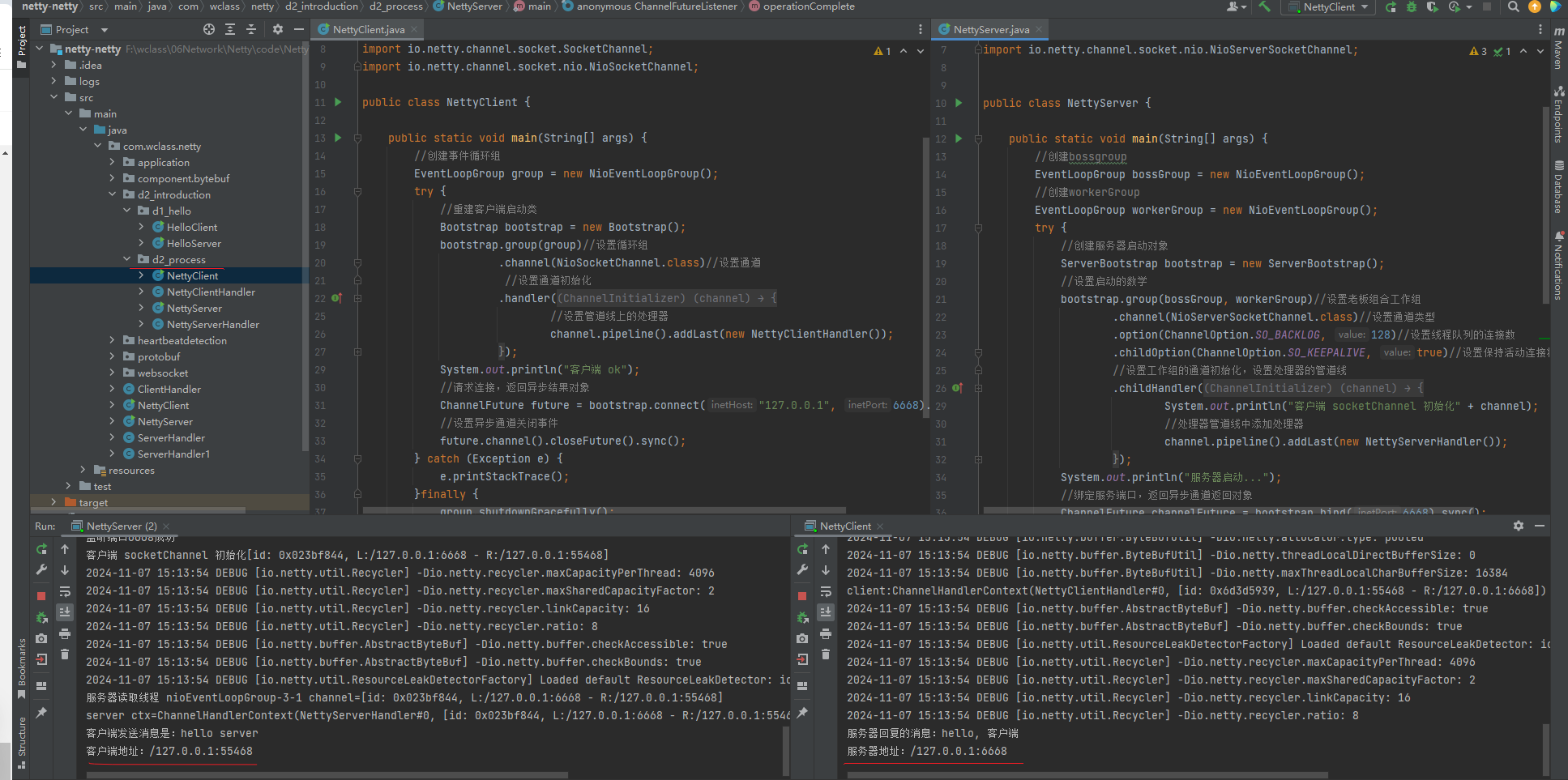
题目:识别数字0-9,做梯度检测来验证是否在梯度下降过程中存在问题,并可视化隐藏层
代码:
import numpy as np
import scipy.io as sio
import matplotlib.pyplot as plt
from scipy.optimize import minimizedef sigmoid(z):return 1/(1+np.exp(-z))def sigmoid_derivation(z): # sigmoid函数求导return sigmoid(z)*(1-sigmoid(z))def one_hot(raw_y):result = []for i in raw_y: # 1-10y_temp = np.zeros(10)y_temp[i-1] = 1result.append(y_temp)return np.array(result) #返回成数组的格式def sequence(theta1,theta2): #序列化return np.append(theta1.flatten(), theta2.flatten()) # 方便后续调用scipy库方便, minimize要求初始化参数x0# 只有1列,def return_sequence(theta_sequence): #解序列化theta1 = theta_sequence[:25*401].reshape(25, 401) # 解序列化 保证后续矩阵运算维度是一致的theta2 = theta_sequence[25*401:].reshape(10, 26)return theta1, theta2def forward_propagation(theta_sequence, X):theta1, theta2 = return_sequence(theta_sequence)a1 = Xz2 = a1@theta1.Ta2 = sigmoid(z2)a2 = np.insert(a2, 0, values=1, axis=1)z3 = a2@theta2.Th = sigmoid(z3)return a1, z2, a2, z3, hdef cost_function(theta_sequence, X, y):a1, z2, a2, z3, h = forward_propagation(theta_sequence, X)J = (-np.sum(y*np.log(h)+(1-y)*np.log(1-h)))/len(X)return Jdef reg_cost_function(theta_sequence, X, y, l=1):first = np.sum(np.power(theta1[:, 1:], 2))second =np.sum(np.power(theta2[:, 1:], 2))reg = (first + second) * l / (2 * len(X))return reg + cost_function(theta_sequence, X, y)def gradient(theta_sequence, X, y): # 反向传播计算误差deltatheta1, theta2 = return_sequence(theta_sequence)a1, z2, a2, z3, h = forward_propagation(theta_sequence, X)d3 = h-yd2 = d3@theta2[:,1:]*sigmoid_derivation(z2)D2 = (d3.T@a2) / len(X)D1 = (d2.T@a1) / len(X)return sequence(D1, D2)def reg_gradient(theta_sequence, X, y, l=1): # 正则化D = gradient(theta_sequence, X, y)D1, D2 = return_sequence(D)theta1, theta2 = return_sequence(theta_sequence)D1[:, 1:] = D1[:, 1:] + theta1[:, 1:] * l / len(X)D2[:, 1:] = D2[:, 1:] + theta2[:, 1:] * l / len(X)return sequence(D1, D2)def neutral_network(X, y, l):init_theta = np.random.uniform(-0.5, 0.5, 10285) # 随机化初始值,避免全为0结果只有一个特征res = minimize(fun=reg_cost_function,x0=init_theta,args=(X, y, l),method='TNC',jac=reg_gradient,options={'maxiter': 300}) # 设置最大迭代次数为300return resdata = sio.loadmat('ex4data1.mat')
raw_x = data['X']
raw_y = data['y']
print(raw_y)
X = np.insert(raw_x, 0, values=1, axis=1) # 添加偏置单元
print(X.shape)y = one_hot(raw_y)
print(y)
print(y.shape)theta = sio.loadmat('ex4weights.mat')
theta1 = theta['Theta1']
theta2 = theta['Theta2']
print(theta1.shape)
print(theta2.shape)theta_sequence = sequence(theta1, theta2)print(reg_cost_function(theta_sequence, X, y, l=1))l = 10
res = neutral_network(X, y, l)
raw_y = data['y'].reshape(5000) # 降为一维方便后面进行梯度检验时的比较
a1, z2, a2, z3, h = forward_propagation(res.x, X)
y_pred = np.argmax(h, axis=1)+1 # 取最大
accrancy = np.mean(y_pred == raw_y)
print(accrancy)def hidden_layer(theta):theta1, theta2 = return_sequence(theta)hidden_layer = theta1[:, 1:]fig, ax = plt.subplots(nrows=5, ncols=5, figsize=(8, 8), sharex=True, sharey=True)for r in range(5):for c in range(5):ax[r, c].imshow(hidden_layer[5 * r + c].reshape(20, 20).T,cmap='gray_r')plt.xticks([])plt.yticks([])plt.show()hidden_layer(res.x)
输出:
[[10][10][10]...[ 9][ 9][ 9]]
(5000, 401)
[[0. 0. 0. ... 0. 0. 1.][0. 0. 0. ... 0. 0. 1.][0. 0. 0. ... 0. 0. 1.]...[0. 0. 0. ... 0. 1. 0.][0. 0. 0. ... 0. 1. 0.][0. 0. 0. ... 0. 1. 0.]]
(5000, 10)
(25, 401)
(10, 26)
0.38376985909092365
0.9394进程已结束,退出代码0
可视化隐藏层
总结:与之前相比,这次代码中数学的运算多了很多,尤其是偏导部分;注意写代码前要多推导数学运算的过程不要出现差错;有所改进的是跟之前在minimize中加flatten相比,直接添加了一个函数对参数进行序列化操作来方便调用scipy库。
作业订正参考:【作业讲解】编程作业4:神经网络(2)(上)_哔哩哔哩_bilibili