目录
题目链接:118. 杨辉三角 - 力扣(LeetCode)
题目描述
示例
提示:
解法一:利用特性构建杨辉三角
1. 结果存储结构:
2. 初始化和循环遍历每一层:
3. 构建每一层:
4. 填充中间的元素:
5. 添加最后一个元素:
6. 将当前行添加到结果集:
7. 更新 len:
8. 返回最终结果:
Java写法:
C++写法:
运行时间
时间复杂度和空间复杂度
解法二:递归
递归思路:
Java写法:
C++写法:
关键变化:
运行时间
时间复杂度和空间复杂度
解法三:不讲武德版(面向测试用例编程)
Java写法:
运行时间
总结
解法总结:
小结:

题目链接:118. 杨辉三角 - 力扣(LeetCode)
注:下述题目描述和示例均来自力扣
题目描述
给定一个非负整数 numRows,生成「杨辉三角」的前 numRows 行。
在「杨辉三角」中,每个数是它左上方和右上方的数的和。
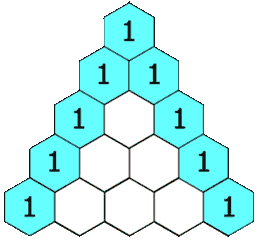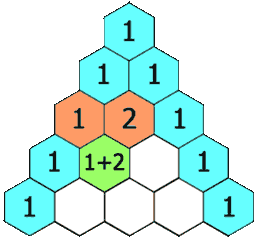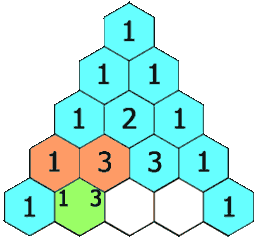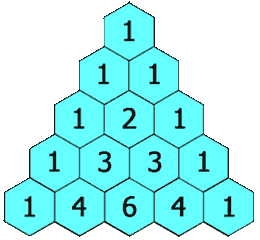
示例
示例 1:
输入: numRows = 5 输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]
示例 2:
输入: numRows = 1 输出: [[1]]
提示:
1 <= numRows <= 30

解法一:利用特性构建杨辉三角
1. 结果存储结构:
- 这里使用
List<List<Integer>>来存储杨辉三角的每一行数据。res是最终返回的结果集,它是一个二维列表,存放着每一层的数组。
2. 初始化和循环遍历每一层:
len代表当前层的元素个数。每一层的元素个数是递增的,从 1 开始。numRows是杨辉三角的行数,for循环遍历每一行,numberOfLayers代表当前的行索引(从 0 开始)。
3. 构建每一层:
- 每一行是一个
List<Integer>,并且我们首先将1加入到列表中,因为每一行的第一个元素总是1。
4. 填充中间的元素:
- 中间的元素是由上一行的相邻两个元素相加得到的。
res.get(numberOfLayers - 1)取得上一行的数据,然后get(i)取得上一行中第i个元素,get(i - 1)取得上一行中第i - 1个元素,将它们相加,并将结果添加到当前行one中。 i从1开始,到len - 2,因为第一个和最后一个元素已经加到one中了。
5. 添加最后一个元素:
- 除了第一行,所有的行最后一个元素都是
1,所以通过判断当前层是不是第一层来决定是否添加最后一个元素1。
6. 将当前行添加到结果集:
- 每次生成一行后,将它添加到
res中。
7. 更新 len:
- 每次处理完一层后,
len增加 1,因为下一行的元素个数比当前行多一个。
8. 返回最终结果:
- 最终返回
res,即生成的完整杨辉三角。
Java写法:
class Solution {public List<List<Integer>> generate(int numRows) {// 定义出返回的结果集List<List<Integer>> res = new ArrayList<>();// 1// 1 1// 1 2 1// 1 3 3 1// 1 4 6 4 1// 那么其实我们把杨辉三角抽象到我们的二维数组(链表)中// 就是边上的数都是1,中间的数,是上一个数组中=>当前索引的数+前一个索引的数// 定义出 len 表示一层的数量 1,2,3...int len = 1;// numberOfLayers表示层数for(int numberOfLayers = 0; numberOfLayers < numRows; numberOfLayers++){// 记录一层的数据List<Integer> one = new ArrayList<>();one.add(1);int i = 1;for(;i < len - 1; i++){// 将两数相加再放入列表one.add(res.get(numberOfLayers - 1).get(i) + res.get(numberOfLayers - 1).get(i - 1));}if(numberOfLayers != 0){one.add(1);}res.add(one);len++;}return res;}
}C++写法:
C++ 中没有 List 类型,通常使用 vector 来替代。同时,在 C++ 中我们也使用 vector<vector<int>> 来表示二维数组。代码结构与 Java 类似。
#include <vector>
using namespace std;class Solution {
public:vector<vector<int>> generate(int numRows) {// 定义返回的结果集vector<vector<int>> res;// numberOfLayers表示层数for (int numberOfLayers = 0; numberOfLayers < numRows; numberOfLayers++) {// 记录当前行的数据vector<int> one;one.push_back(1); // 每行的第一个元素为1// 中间元素是上一行的相邻元素之和for (int i = 1; i < numberOfLayers; i++) {one.push_back(res[numberOfLayers - 1][i - 1] + res[numberOfLayers - 1][i]);}// 每行的最后一个元素为1(除了第一行)if (numberOfLayers > 0) {one.push_back(1);}// 将当前行添加到结果集res.push_back(one);}return res;}
};
运行时间

时间复杂度和空间复杂度
-
时间复杂度:
- 外层循环遍历每一行,循环次数为
numRows,即O(n)。 - 内层循环对每一行的元素进行处理,每一行最多有
numRows个元素,最坏情况下是O(n)。 - 因此,时间复杂度是
n是杨辉三角的行数。
- 外层循环遍历每一行,循环次数为
-
空间复杂度:
- 结果
res存储了每一行的元素,空间复杂度为
- 结果
 |  |

解法二:递归
递归思路:
- 递归起始:初始时,杨辉三角的第一行
[1]被添加到list中。 - 递归生成每一行:
- 每次递归调用都会生成当前行并添加到
list中。 - 当前行通过上一行的元素计算得出,首先是第一个
1,然后是中间的元素,通过相邻两个元素之和得出,最后是尾部的1。
- 每次递归调用都会生成当前行并添加到
- 递归终止:当生成的行数等于
numRows时,停止递归。
Java写法:
class Solution {public List<List<Integer>> generate(int numRows) {// 初始化存储杨辉三角的二维列表List<List<Integer>> list = new ArrayList<>();// 初始化第一行 [1]List<Integer> arr = new ArrayList<>();arr.add(1);list.add(arr);// 如果只需要生成第一行,直接返回if(numRows == 1) return list;// 否则递归生成剩下的行method(numRows, list, arr);return list;}void method(int number, List<List<Integer>> list, List<Integer> arr){// 如果已经生成了所需的行数,则停止递归if(list.size() == number){return;}// 初始化新的一行List<Integer> newArr = new ArrayList<>();newArr.add(1); // 每一行的第一个元素是1// 计算中间的元素,通过上一行相邻元素之和填充for(int i = 0; i < arr.size() - 1; i++) {newArr.add(arr.get(i) + arr.get(i + 1));}newArr.add(1); // 每一行的最后一个元素是1list.add(newArr); // 添加当前行到结果中// 递归生成下一行method(number, list, newArr);}
}
C++写法:
关键变化:
vector替换List:C++ 中没有List类,改为使用vector,这是 C++ 标准库中最常用的动态数组类型。push_back替代add:C++ 的vector使用push_back()方法来添加元素,替代 Java 中的add()方法。- 引用传递:为了提高性能,
method函数中的list和arr都采用了引用传递(vector<int>&和vector<vector<int>>&),这样可以避免复制数据。
#include <vector>
using namespace std;class Solution {
public:vector<vector<int>> generate(int numRows) {// 初始化存储杨辉三角的二维向量vector<vector<int>> list;// 初始化第一行 [1]vector<int> arr = {1};list.push_back(arr);// 如果只需要生成第一行,直接返回if (numRows == 1) return list;// 否则递归生成剩下的行method(numRows, list, arr);return list;}private:void method(int number, vector<vector<int>>& list, vector<int>& arr) {// 如果已经生成了所需的行数,则停止递归if (list.size() == number) {return;}// 初始化新的一行vector<int> newArr = {1}; // 每一行的第一个元素是1// 计算中间的元素,通过上一行相邻元素之和填充for (int i = 0; i < arr.size() - 1; i++) {newArr.push_back(arr[i] + arr[i + 1]);}newArr.push_back(1); // 每一行的最后一个元素是1list.push_back(newArr); // 添加当前行到结果中// 递归生成下一行method(number, list, newArr);}
};
运行时间
就离谱,测试用例比较有特点导致的,多跑几次可以遇到一次0ms 的情况,这种操作在力扣不是第一次出现了,居然比下面的不讲武德版本还快无语了![]()

时间复杂度和空间复杂度
- 时间复杂度:
O(n^2),生成杨辉三角时,生成每行的元素需要遍历前一行的元素,所以总时间复杂度为二次方。 - 空间复杂度:
O(n^2),需要存储杨辉三角的所有行,每一行的元素个数是递增的,空间复杂度也是二次方。

解法三:不讲武德版(面向测试用例编程)
这么搞笑的解法,在我看见只有

这么点数据的时候我就发现了,非常抽象哈。
Java写法:
class Solution {public List<List<Integer>> generate(int numRows) {// 直接定义出来所有的数据集Integer[][] a= {{1},{1, 1},{1, 2, 1},{1, 3, 3, 1},{1, 4, 6, 4, 1},{1, 5, 10, 10, 5, 1},{1, 6, 15, 20, 15, 6, 1},{1, 7, 21, 35, 35, 21, 7, 1},{1, 8, 28, 56, 70, 56, 28, 8, 1},{1, 9, 36, 84, 126, 126, 84, 36, 9, 1},{1, 10, 45, 120, 210, 252, 210, 120, 45, 10, 1},{1, 11, 55, 165, 330, 462, 462, 330, 165, 55, 11, 1},{1, 12, 66, 220, 495, 792, 924, 792, 495, 220, 66, 12, 1},{1, 13, 78, 286, 715, 1287, 1716, 1716, 1287, 715, 286, 78, 13, 1},{1, 14, 91, 364, 1001, 2002, 3003, 3432, 3003, 2002, 1001, 364, 91, 14, 1},{1, 15, 105, 455, 1365, 3003, 5005, 6435, 6435, 5005, 3003, 1365, 455, 105, 15, 1},{1, 16, 120, 560, 1820, 4368, 8008, 11440, 12870, 11440, 8008, 4368, 1820, 560, 120, 16, 1},{1, 17, 136, 680, 2380, 6188, 12376, 19448, 24310, 24310, 19448, 12376, 6188, 2380, 680, 136, 17, 1},{1, 18, 153, 816, 3060, 8568, 18564, 31824, 43758, 48620, 43758, 31824, 18564, 8568, 3060, 816, 153, 18, 1},{1, 19, 171, 969, 3876, 11628, 27132, 50388, 75582, 92378, 92378, 75582, 50388, 27132, 11628, 3876, 969, 171, 19, 1},{1, 20, 190, 1140, 4845, 15504, 38760, 77520, 125970, 167960, 184756, 167960, 125970, 77520, 38760, 15504, 4845, 1140, 190, 20, 1},{1, 21, 210, 1330, 5985, 20349, 54264, 116280, 203490, 293930, 352716, 352716, 293930, 203490, 116280, 54264, 20349, 5985, 1330, 210, 21, 1},{1, 22, 231, 1540, 7315, 26334, 74613, 170544, 319770, 497420, 646646, 705432, 646646, 497420, 319770, 170544, 74613, 26334, 7315, 1540, 231, 22, 1},{1, 23, 253, 1771, 8855, 33649, 100947, 245157, 490314, 817190, 1144066, 1352078, 1352078, 1144066, 817190, 490314, 245157, 100947, 33649, 8855, 1771, 253, 23, 1},{1, 24, 276, 2024, 10626, 42504, 134596, 346104, 735471, 1307504, 1961256, 2496144, 2704156, 2496144, 1961256, 1307504, 735471, 346104, 134596, 42504, 10626, 2024, 276, 24, 1},{1, 25, 300, 2300, 12650, 53130, 177100, 480700, 1081575, 2042975, 3268760, 4457400, 5200300, 5200300, 4457400, 3268760, 2042975, 1081575, 480700, 177100, 53130, 12650, 2300, 300, 25, 1},{1, 26, 325, 2600, 14950, 65780, 230230, 657800, 1562275, 3124550, 5311735, 7726160, 9657700, 10400600, 9657700, 7726160, 5311735, 3124550, 1562275, 657800, 230230, 65780, 14950, 2600, 325, 26, 1},{1, 27, 351, 2925, 17550, 80730, 296010, 888030, 2220075, 4686825, 8436285, 13037895, 17383860, 20058300, 20058300, 17383860, 13037895, 8436285, 4686825, 2220075, 888030, 296010, 80730, 17550, 2925, 351, 27, 1},{1, 28, 378, 3276, 20475, 98280, 376740, 1184040, 3108105, 6906900, 13123110, 21474180, 30421755, 37442160, 40116600, 37442160, 30421755, 21474180, 13123110, 6906900, 3108105, 1184040, 376740, 98280, 20475, 3276, 378, 28, 1},{1, 29, 406, 3654, 23751, 118755, 475020, 1560780, 4292145, 10015005, 20030010, 34597290, 51895935, 67863915, 77558760, 77558760, 67863915, 51895935, 34597290, 20030010, 10015005, 4292145, 1560780, 475020, 118755, 23751, 3654, 406, 29, 1}};// 装填数据集到我们的list集合之中List<List<Integer>> list = new ArrayList<>();for (int i = 0; i < numRows; i++) {list.add((List<Integer>)Arrays.asList(a[i]));}// 直接返回即可return list;}
}运行时间

没啥提升我是没有想到的,过于离谱了还是。
总结
解法总结:
-
解法一(迭代构建):
- 使用二维数组
List<List<Integer>>存储杨辉三角。 - 从第一行
[1]开始,逐行构建,每行的首尾元素为1,中间的元素为上一行相邻两个元素之和。 - 时间复杂度:
O(n^2),空间复杂度:O(n^2)。
- 使用二维数组
-
解法二(递归构建):
- 递归地生成每一行,通过上一行的元素计算当前行的值。
- 时间复杂度:
O(n^2),空间复杂度:O(n^2)。
-
解法三(硬编码):
- 直接定义一个二维数组,包含了杨辉三角的所有行。
- 适用于测试用例数较少的情况,时间复杂度和空间复杂度均为常数级别。
小结:
- 解法一和解法二通过动态计算逐行生成杨辉三角,适合处理较大的
numRows值。 - 解法三虽然效率较高,但不具通用性,只适用于有限的
numRows值。