机器学习4_支持向量机_核函数—

机器学习4_支持向量机_核函数——MOOC

核函数的定义

引入了映射 $\varphi \left ( X \right )$ 后

最小化： $\frac{1}{2}\left \| \omega \right \|^2+C\displaystyle\Sigma_{i=1}^N\delta _i$ 或 $\frac{1}{2}\left \| \omega \right \|^2+C\Sigma _{i=1}^N\delta _i^2$

限制条件：

（1） $\delta _i\geq 0,\left ( i=1,2,..., N \right )$

（2） $y_i\left [\omega ^T\varphi (X_i)+b \right ]\geq 1-\delta _i,\left ( i=1\sim N \right )$

具体研究 $\varphi \left ( X_i \right )\Rightarrow$ 引入 核函数（Kernel Function）

Vladimir Naumovich Vapnik 指出，可以不用知道 $\varphi \left ( X \right )$ 的具体形式。

对任意两个向量 $X_1,X_2$ ，有 $K(X_1,X_2)=\varphi (X_1)^T\varphi (X_2)$

定义 $K(X_1,X_2)$ 为核函数，这是一个实数

维度相同的列向量 $\varphi (X_1)^T\varphi (X_2)$ ， $\varphi (X_1),\varphi (X_2)$ 是维度相同的列向量， $\varphi (X_1)$ 的转置是一个行向量。行向量乘以一个列向量就得到了一个实数。

核函数以及低维到高维的映射 $\varphi \left ( X \right )$ 的相互关系

例1：已知 $\varphi \left ( X \right )$ 求 K

假设：

$\varphi \left ( X \right )$ 是一个将二维向量映射为三维向量的映射

$X=[x_1,x_2]^T$

$\varphi \left ( X \right )=\varphi ([x_1,x_2]^T)=[x_1^2,x_1x_2,x_2^2]$

假设有两个二维向量

$X_1=[x_{11},x_{12}]^T$ ， $X_2=[x_{21},x_{22}]^T$

根据前面的定义， $\varphi (X_1)=[x_{11}^2,x_{11}x_{12},x_{12}^2]$ ， $\varphi (X_2)=[x_{21}^2,x_{21}x_{22},x_{22}^2]$

那么

$K(X_1,X_2)=\varphi (X_1)\varphi (X_2)$

 $=[x_{11}^2,x_{11}x_{12},x_{12}^2][x_{21}^2,x_{21}x_{22},x_{22}^2]^T$

 $=x_{11}^2x_{21}^2+x_{11}x_{12}x_{21}x_{22}+x_{12}^2x_{22}^2$

例2：已知核函数 K 求映射 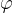$\varphi$ 的例子

假设：

$X$ 是一个二维向量

这里有两个分量

$X_1=[x_{11},x_{12}]^T$ ， $X_2=[x_{21},x_{22}]^T$

假设：

$K(X_1,X_2) =(x_{11}x_{12}+x_{21}x_{22}+1)^2$

 $=x_{11}^2x_{21}^2+x_{12}^2x_{22}^2+1+2x_{11}x_{12}x_{21}x_{22}+2x_{11}x_{12}+2x_{21}x_{22}$

$=\varphi (X_1)^T\varphi (X_2)$

假设：

$X=[x_1,x_2]^T$

$\varphi \left ( X \right )=\varphi ([x_1,x_2]^T)=[x_1^2,x_2^2,1,\sqrt{2}x_1x_2,\sqrt{2}x_1,\sqrt{2}x_2]$

核函数 K 求映射 $\varphi$ 是一一对应的关系

核函数的形式不能随意的取

$\Downarrow$ 满足一定的条件

两个 $\varphi$ 内积的形式

支持向量机优化问题

$K(X_1,X_2)$ 能写成 $\varphi (X_1)^T\varphi (X_2)$ 的充要条件

（1） $K(X_1,X_2)=K(X_2,X_1)$ （交换性）

（2） $\forall C_i(i=i\sim N),\forall N$ 有 $\sum^{N}_{i=1}\sum^{N}_{j=1}C_iC_jK(X_iX_j)\geq 0$ （半正定性）

K 满足交换性和半正定性 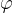$\Rightarrow$ $\varphi$ 内积的形式

例如：可以证明

高斯核函数： $K(X_1,X_2)=e^{-\frac{\left \| X_1-X_2\right \|^2}{2\sigma ^2}}$

这是满足：Mercer's Theorem 定理

$K(X_1,X_2)$ 可以被写为 $\varphi (X_1)^T\varphi (X_2)$ 的形式。

但我们不能知道 $\varphi \left ( X \right )$ 的显式，但可以通过一些方法知道 $\omega ^T\varphi \left ( X \right )+b$ 的值。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.xdnf.cn/news/7303.html

如若内容造成侵权/违法违规/事实不符，请联系一条长河网进行投诉反馈，一经查实，立即删除！

机器学习4_支持向量机_核函数——MOOC

核函数的定义