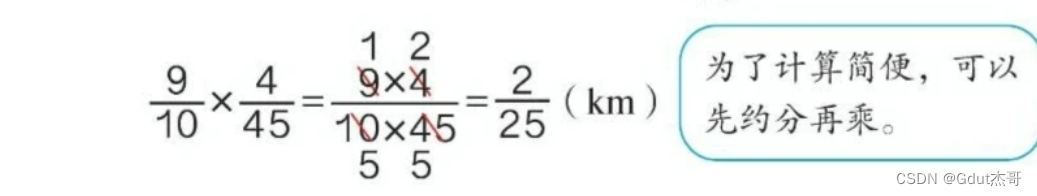一、
很久很久以前,在一个只认识整数和小数的国度,有一个很残暴的国王提了一个要求:要是不能表示出把一段1米的绳子三等分后的大小,就要把所有的大臣杀掉。
1➗3 = 0.333······,怎么办呀?怎么办呀?
袁qy大臣在收到圣旨后慌得上串下跳,没日没夜地算,头都快秃了。
(秃头~~~)
二、
“听说在广工山可以找到阿拉丁神灯,念三遍“袁qy爱数学,袁qy真爱数学,袁qy真的很爱数学”,就会从神灯里冒出一位神仙,名叫杰哥,他或许能化解这场危机”,人们议论纷纷。
三、
“袁壮士,祝你一路平安”,人们纷纷来给袁庆茵大臣送行。
“风萧萧兮易水寒,这一去,不知何时能归,各位,就此别过吧”,袁qy拱手别过。
一路上,袁壮士看到了许多未解谜题?
比如:0.9999······=1;
比如:约分与通分(数学的统一美)
比如:配凑(大千世界,分分合合)
比如:对分数的深刻理解
比如:如何速算0.875×0.8+0.75×0.4+0.5×0.2
比如:工程问题
比如:还有各种复杂的计算难题······
袁qy越觉自己使命重大,或许将会颠覆一整个国度的认知。
四、
“袁qy爱数学,袁qy真爱数学,袁qy真的很爱数学”,袁qy找到了神灯,并默念咒语。“呼呼呼······”,忽然一阵烟飘过,杰哥浮现在袁qy面前。
没有看错,就是眼前这一位。😄
杰哥大手一挥,直接把1÷3写成了三分之一,“既然除不尽,那就把除号留着吧,但是为了方便,我们把除号用一根横线表示”。
袁:“先生真乃造物主也,我再也不用写好多个3,写到头秃了。在我们的国度都没有这样的数,只有整数和小数,那怎么理解这样的数呢?”
五、
杰:
从除法的角度理解,是1÷3,根据同乘同除商不变,所以等于2÷6,这就是约分和通分的本质。
从占比的角度理解,是三份中的一份。
袁:
“厉害呀,先生,这样我们国家的人民也将拥有改造数字的能力,如1÷3×6=2÷6×6”,
又如2÷9×99=22÷99×99。
同理,“22÷99×9=2÷9×9”。
把👆的写成分数的形式,能更明显感受到它的神奇。(数学统一美)
杰:
哈哈,是的,约分的本质是分子和分母有共同的因数(拆砖块);通分的本质是同乘一个因数(补砖块)。
所以化简49分之119也是去找他们共同的因数。(记不记得辗转相除法)
杰:
另外从占比的角度,或许能深刻理解200-⅔,就像200个蛋糕,你吃了其中一个的⅔,那不就剩199和⅓吗?
所以,可以用带分数199⅓表示199+⅓。
六、
袁:
先生,这么棒的东西有没有像小数和整数那样的运算性质?
杰:
那是当然的啦。像那些什么乘法分配律什么的都适用。另外,当你算⅓+½时,对于这种分母不同的,应该先通分,使其基数一样,也就是说分母一样。
形象理解:
与其拿两个蛋糕,一个切⅓,另外一个切½,然后拼起来。
还不如直接把一个蛋糕切成6份,取其中5份,即⅓+½=六分之二+六分之三
减法也一样,1-⅓其实就是一分之一减三分之一,也就是三分之三减三分之一,或者从蛋糕只剩下⅔来理解。
七、
“先生……”,忽然眼前出现一阵烟雾,神仙回到了神灯中,袁qy大臣认为是不是自己诚意不够,又念了几遍咒语,“……爱数学…爱数学…”。
这时神灯变成了一幅幅画卷。
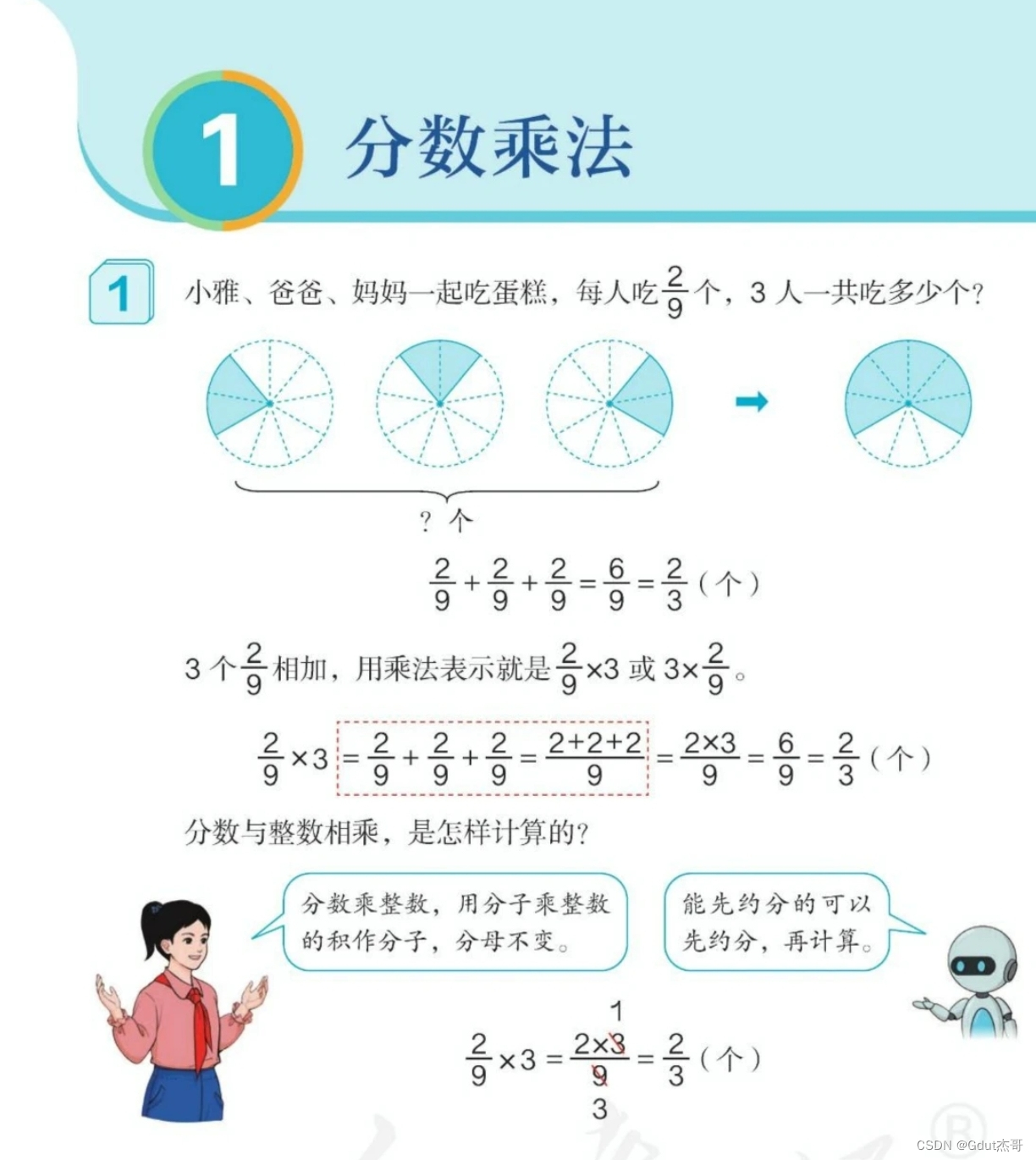
“噢,怪不得分数乘整数的时候要把整数乘到分子上去”,袁大臣捋了捋胡子说。
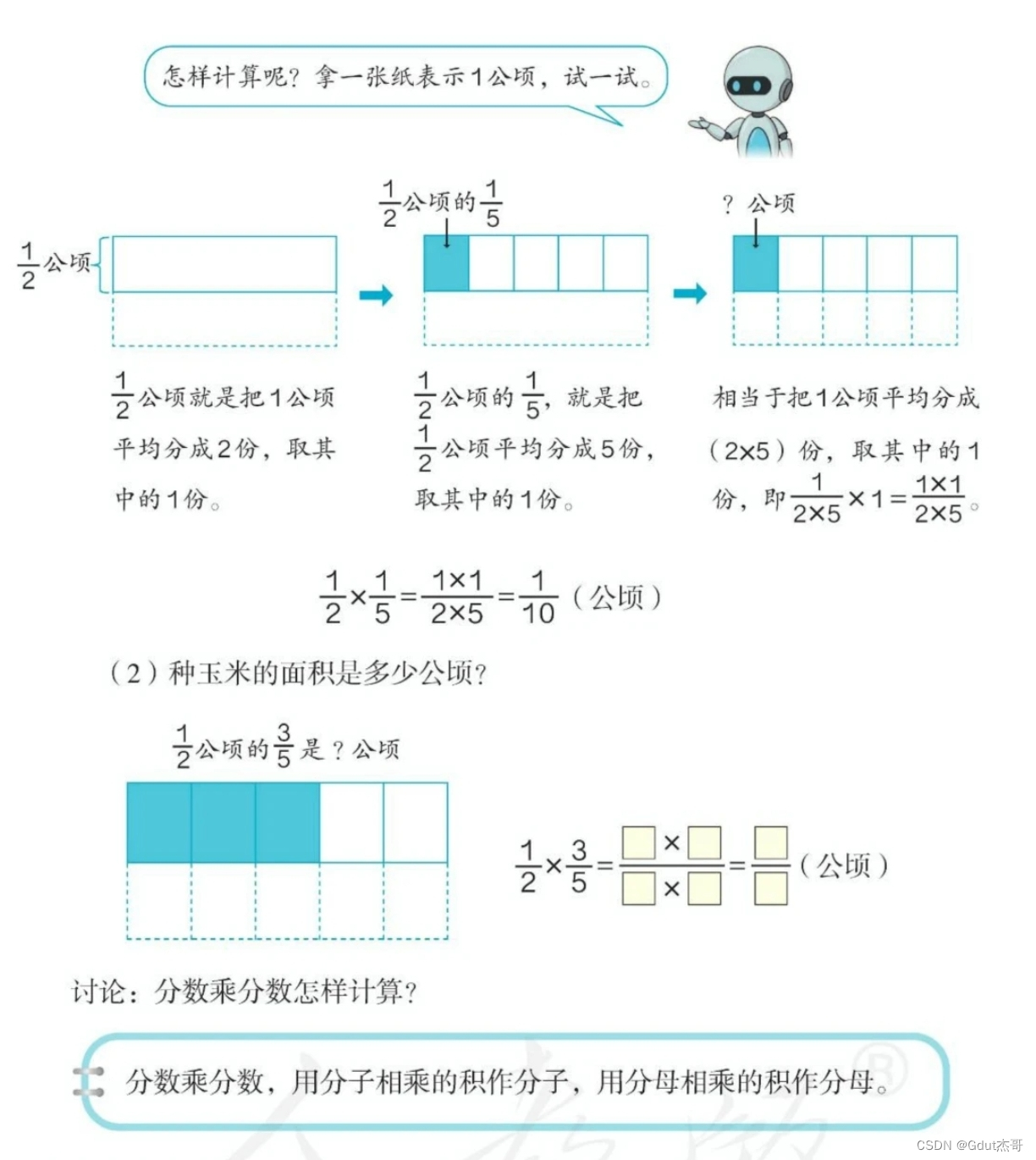
“好一个分子乘分子,分母乘分母”,袁大臣拍手叫好。
“年轻人,请记住,我预言到你是拯救世界的人,在你的冒险中,我将赋予你几个绝招……”,一阵回声响彻天际。
“谁……是你吗?先生。”袁qy四处张望。
“是的,爱数学,将是你冒险中的最大的武器,去吧,世界需要你。”
绝招一第一式:(遇到带分数,可以整数和分数分离)
如:23⅓×3=(23+⅓)×3
(不要浮躁,年轻人,这个例子看似简单,但其蕴含的数学思想是需要你好好体会的)
绝招一第二式:
直接对过程约分,不用算出结果再约分(约分的本质就是有公因数)
绝招二:(对立相生)
“世界是对立统一的,黑白相生、大小相对……”。
如:
1、99⅓除了拆成99+⅓,还可以是100-⅔
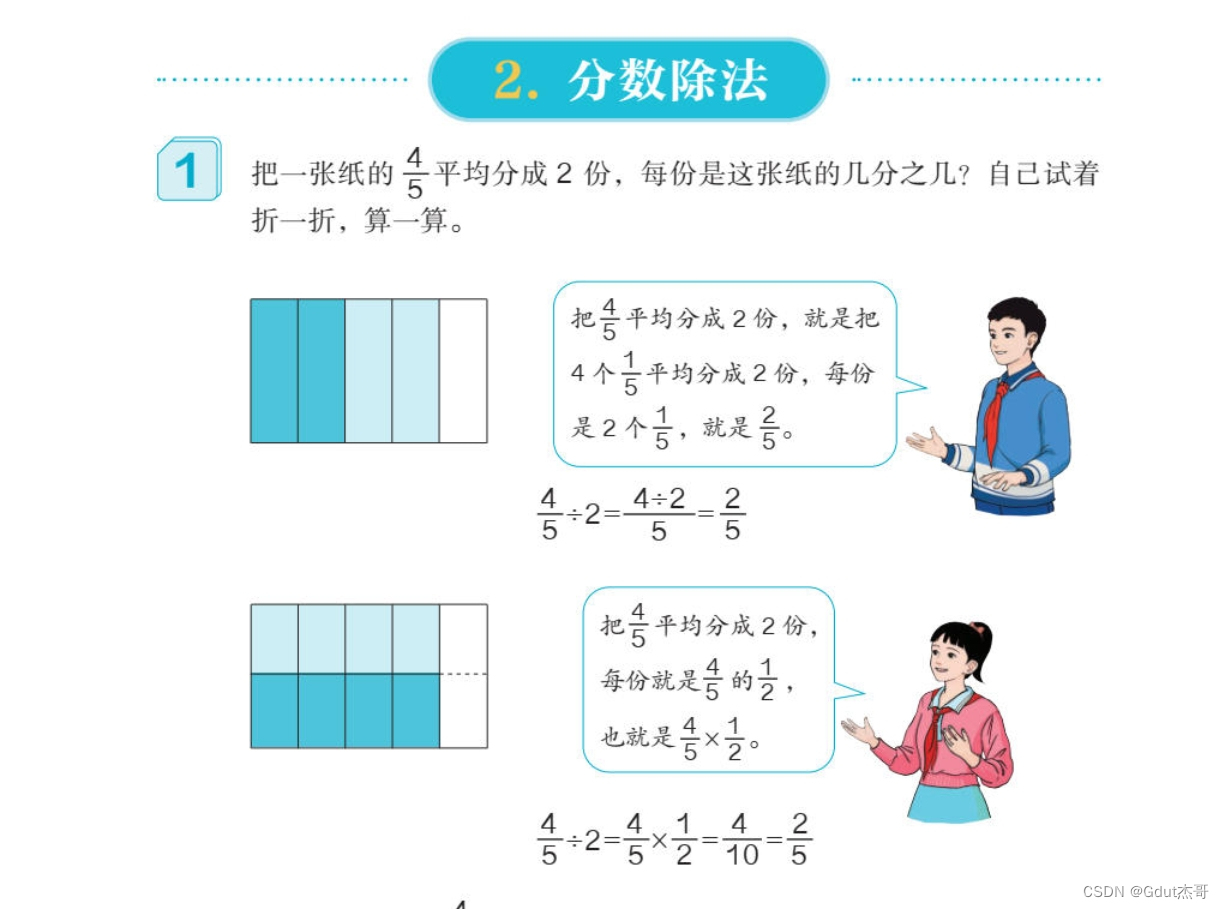
2、既然有乘法,那么除法是怎么样的呢?
噢,原来,除以一个分数等于乘上这个分数的倒数。