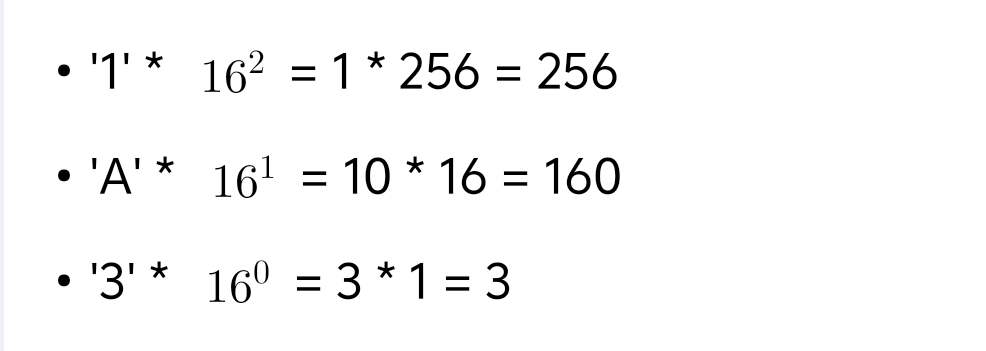目录
1 信息与编码
1.1 什么是信息?
1.2 什么是编码?
2 数制和码制
2.1 数制
3 一些基本概念
3.1 位(bit)
3.2 字节(byte)
3.3 数据量的大小表示符号
4 二进制
4.1 二进制简介
4.2 二进制的转换
4.2.1 二进制转换为十进制
4.2.2 十进制转换为二进制
4.2.3 二进制转换为八进制
4.2.4 二进制转换为十六进制
4.2.5 八进制转换十六进制
4.2.6 八进制和十六进制转换为十进制
4.2.7 十进制转换为八进制和十六进制
1 信息与编码
1.1 什么是信息?
信息是为通过数据表示和传递且具有一定含义的内容。信息一般通过文字、数字、图片、视频等方式来进行表达。
1.2 什么是编码?
编码是将信息以一种格式转换为另一种格式的方式。
在编码时,需要注意以下几个要点:
- 编码的方式
- 效率
- 安全性
- 可靠性
2 数制和码制
数制:表示数量的规律。
码制:表示事物的规律。
2.1 数制
数制重要的的两:(1)每一位的构成(2)相加时从低到高向前进位的方式(减法借位同理)。
例如对于一个普通的二进制数:

对于上面这种二进制数,二进制数由0和1组成,在相加的时低位相加若等于2则本位清0后高一位的数位加1,可以简称为“逢二进一”(二进制的减法同理)。
3 一些基本概念
3.1 位(bit)
位是信息量的基本单位,在十进制中,每个位可以由0~9来表示,而在二进制中,每一个位数只能由0或1来表示。位是所有数字信息中在计算机内部表示和处理的最基本方式。
3.2 字节(byte)
在二进制中,8个bit组成一个字节,一共可以表示256中状态,字节一般使用B来表示,例如4B表示4个字节。
3.3 数据量的大小表示符号
K(千):表示2的10次方,
M(兆):表示2的20次方,
G(吉):表示2的30次方,
T(太):表示2的40次方,
4 二进制
4.1 二进制简介
二进制是一种数字的表示方法,0和1,用来表示数值。
例如对于这个二进制数:

很明显上面是一个8位二进制数,由0和1组成。可以通过写成提示这是个二进制数。
4.2 二进制的转换
4.2.1 二进制转换为十进制
(1)整数
将二进制数转换为十进制数,从右往左数第n位数,该位的数乘以2的(n-1)次方,即该位为1,为1×2^(n-1),该位为0,则0×2^(n-1)。

将其转换为10进制的数的公式如下所示

因此我们可以得到上面那一串数字的十进制数值为:
(2)小数
小数也能将其转换为二进制数,小数点后从左向右数第n位,则乘以2的(-n)次方。如下图所示:

对于上图中的小数,对其进行计算:
再例如二进制小数,将其转换为十进制
再例如二进制小数,将其转换为十进制
通过对于整数和小数的学习,那么对于正的二进制数,均能用十进制来表示它,例,将其转换为十进制数为:
4.2.2 十进制转换为二进制
(1)整数
将十进制转换为二进制,可以由整数的转换得:

由上图可以看到,将十进制数除以2所得的余数;若上面所得的商不为0,再将所得的商再除以2得到
,这样依次类推下去,最终得到一个
,一系列的数,再将其从
到
依次从左往右进行排列,得到一个最终的二进制数
。
例如,有一个十进制数
214除以2得到商107,余数0,记为;
107除以2得到商53,余数1,记为;
53除以2得到商26,余数1,记为;
26除以2得到商13,余数0,记为;
13除以2得到商6,余数1,,记为;
6除以2得到商3,余数0,记为;
3除以2得到商1,余数1,记为;
1除以2得到商0,余数1,记为;
用图片来表示为:

再将上面的内容按照,进行排列得到二进制数11010110,再将其进行验算:
(2)小数
与整数一样,小数也可以由十进制转换为二进制。将十进制小数乘以2所得的数进行取整,得到;如果上面结果不为1,取小数部分乘以2所得的数进行取整,记为
;...若第n位数乘以2所得结果为1,那么第n位记为
,且
。这是将
从左到右依次排列,最终该数的小数部分为:
。
例如十进制数0.65625,将其转换为二进制数的过程为:
0.65625乘以2得到1.3125,取整得到1,记作,取小数部分0.3125不为0;
0.3125乘以2得到0.625,取整得到0,记作,取小数部分0.625不为0;
0.625乘以2得到1.25,取整得到1,记作,取小数部分0.25不为0;
0.25乘以2得到0.5,取整得到0,记作,取小数部分0.5不为0;
0.5乘以2得到1,取整得到1,记作,小数部分为0,结束。
因此0.65625转换为二进制数为0.10101,进行验算得:
上面过程的示意图如下所示:

将二进制小数转换为整数时会出现两种情况,首先第一种是能够处理完全的,例如十进制数0.25,0.625。将转换为二进制数为:,
。但是同时也会出现另一种情况,即不能完全表示这个十进制整数。例如十进制的数0.3,将0.3转换为二进制数的过程如下所示:
0.3乘以2得到0.6,取整得到0,记作,取小数部分0.6不为0;
0.6乘以2得到1.2,取整得到1,记作,取小数部分0.2不为0;
0.2乘以2得到0.4,取整得到0,记作,取小数部分0..4不为0;
0.4乘以2得到0.8,取整得到0,记作,取小数部分0.8不为0;
0.8乘以2得到1.6,取整得到1,记作,取小数部分0.6不为0;
......
通过上面计算过程可以看到,对于十进制数0.3,可以看到不能完全将其表示,即十进制转换为二进制时会转换为一个无线循环二进制小数(有的数转换为二进制时无限不循环小数,例如Π),这种小数不能把它完全表示出来,因此可以精确到某一位。例如将将其转换为二进制小数,精确到小数点后五位,是
。
4.2.3 二进制转换为八进制
同样,二进制也可以转换为八进制和十六进制的数。对于二进制转化为八进制的数可以看到二进制中每三位的转换为一位的八进制数,例如:,
同理,二进制转可以为十六进制,每4位转换为一个十六进制数,,
,
,需要注意的是在一些编程语言(Java、C++、C、Shell等等)可以在十六进制数前面加上0X表示十六进制,例如0X4D,0X3F。
对于四位二进制数,其二进制、八进制和十六进制相互转换表如下所示:
| 二进制 | 八进制 | 十六进制 | 二进制 | 八进制 | 十六进制 |
| 0000 | 00 | 0 | 1000 | 10 | 8 |
| 0001 | 01 | 1 | 1001 | 11 | 9 |
| 0010 | 02 | 2 | 1010 | 12 | A |
| 0011 | 03 | 3 | 1011 | 13 | B |
| 0100 | 04 | 4 | 1100 | 14 | C |
| 0101 | 05 | 5 | 1101 | 15 | D |
| 0110 | 06 | 6 | 1110 | 16 | E |
| 0111 | 07 | 7 | 1111 | 17 | F |
根据上面的表格,我们可以对较长的二进制的数对其进行进行转换。
例如对于二进制数转换为八进制,例如二进制数:,将其从右向左每三位转换为八进制的数,转换过程如下所示:

由上图可知,最低三位的二进制数111转换为八进制的7,中间三位的101转换为八进制的5,最高三位100转换为八进制的4.。
如果二进制位数不是3的倍数,例如,将其转换为八进制数为:

对于最高两位,可以将其在前面补0的操作,例如二进制数10可以在前面补以为变为010,即,因此结果为
。
八进制转换为二进制只需上述相反过程即可。
4.2.4 二进制转换为十六进制
与上面二进制转换为十六进制的规律同理,二进制数同样可以转换为十六进制的数。每四位二进制数转换为一位十六进制的数。例如:

可以看到将上述二进制数转换为十六进制之后,结果如下所示:
同理如下遇到该二进制数所有的数位之和不是4的倍数时,可以在高位补0使该数的位数为4的倍数,例如:,可以数出这个二进制数一共有14位,将其补充到位数为4的倍数时,即16位的数
转换为16进制的数为:
十六进制转换为二进制只需上述相反过程即可。
4.2.5 八进制转换十六进制
对于八进制数来说,一般先将其转换为相对应的二进制数,再将其转换为对应的十六进制数。即:八进制->二进制->十六进制。八进制转换为二进制即一位的八进制转换为三位的二进制数,再将每四位二进制转换为一位十六进制数。例如转换为
,再将该二进制数转换为十六进制为
。因此可以得到
。
十六进制转换为八进制只需上述过程相反过程即可。
4.2.6 八进制和十六进制转换为十进制
八进制和十六进制转换为十进制的原理与二进制转换为十进制类似,例如有这样的八进制数,将其转换为十进制数为:
。
同样对于一个十六进制的数,例如,将其转换为
。
4.2.7 十进制转换为八进制和十六进制
将十进制转换为八进制和十六进制时,可以先将其转换为二进制,再将二进制数转换为八进制或者十六进制数。
或者将十进制转换为二进制中的“除2取余,逆序排列"(小数部分是"乘2取整,正序排列”)变为“除8取余,逆序排列”和“除16取整,逆序排列”。