进制转换的基本概念

进制转换是将一个数从一种基数（进制）转换为另一种基数的过程。例如，将十进制数转换为二进制、八进制或十六进制。

转换过程

以十进制数转换为其他进制为例，转换的基本步骤如下：

• 除以目标进制的基数：将十进制数除以目标进制的基数（例如，二进制的基数是2，八进制的基数是8，十六进制的基数是16）。

• 取余数：获取上一步除法的余数。这个余数将是转换后进制中的最低位（最右边的位）。

• 更新数值：将上一步的商再次除以目标进制的基数，重复这个过程。

• 重复直到商为0：继续这个过程，直到商为0。每次得到的余数将构成转换后的数的每一位，从最低位到最高位。

• 组合余数：将所有得到的余数从最后一个开始向前组合，形成最终的转换结果。

示例

假设我们要将十进制数13转换为二进制：

现在，我们将余数从下到上（从最后一个到第一个）组合起来，得到二进制数1101。

C++代码实现

string convertToBase(int x, int y) {// 初始化一个空字符串，用于存储转换后的结果string result = "";// 定义一个字符串，包含所有可能用到的数字字符，从0到9和A到Fconst string digits = "0123456789ABCDEF";// 当x大于0时，循环继续while (x > 0) {// 计算x除以y的余数，这个余数将是转换后进制的最低位int remainder = x % y;// 将余数转换为对应的字符，并加到结果字符串的前面// 这里使用digits[remainder]来获取余数对应的字符result = digits[remainder] + result;// 更新x的值为商，为下一次循环做准备x /= y;}// 如果结果字符串为空，说明原始的x为0，返回"0"if (result.empty()) {result = "0";}// 返回转换后的字符串结果return result;}

这个函数的工作原理是：

convertToBase 函数接受两个参数： x （十进制数）和 y （目标进制），并返回转换后的字符串。

1. 初始化一个空字符串 result 来存储最终的转换结果。

2. 定义一个常量字符串 digits ，它包含了所有可能用到的数字字符，从'0'到'9'和'A'到'F'，用于将数字转换为对应的字符。

3. 使用 while 循环，只要 x 大于0就继续执行循环体。

4. 在循环体内，首先计算 x 除以 y 的余数，这个余数将用于构建转换后的数字。

5. 然后，使用 digits[remainder] 获取余数对应的字符，并将其添加到 result 字符串的前面。

6. 更新 x 的值为 x 除以 y 的商，为下一次循环做准备。

7. 循环结束后，如果 result 为空，说明原始的 x 为0，因此将 result 设置为"0"。

8. 最后，返回 result 字符串，它是 x 转换为 y 进制后的结果。

这段代码中，x % y计算余数，x /= y更新商，然后将余数转换为字符并添加到结果字符串的前面。这个过程重复进行，直到x变为0。最后，如果结果为空（即输入的数为0），则返回"0"。

注意

在进制转换中，使用字符'A'到'F'是为了表示超过十进制数字'9'的数值。这是因为在二进制、八进制或十六进制等系统中，数值的表示不仅仅局限于0到9这十个数字。

为什么需要'A'到'F'？

• 二进制（Binary）:只使用0和1，不需要'A'到'F'。

• 八进制（Octal）:使用0到7，同样不需要'A'到'F'。

• 十六进制（Hexadecimal）:使用0到9和A到F。在十六进制中，'A'代表10，'B'代表11，依此类推，直到'F'代表15。

十六进制的表示

十六进制是一种基数为16的数制，这意味着每一位可以表示16个不同的值。在十六进制中：

• 0-9 直接对应十进制的0到9。

• A-F 对应十进制的10到15。

例如，十六进制数"1A3"转换为十进制的计算方式如下：

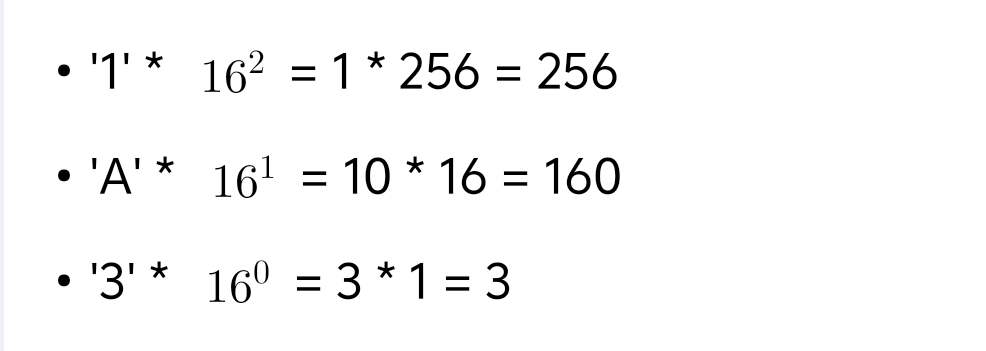
将这些值相加得到：256+160+3=419。

为什么在进制转换函数中包含'A'到'F'？

在编写一个通用的进制转换函数时，我们通常希望这个函数能够处理所有可能的进制，包括十六进制。因此，我们在函数中包含一个字符串digits = "0123456789ABCDEF"，这样无论转换到哪个进制（至少到16进制），我们都能从这个字符串中获取正确的字符来表示每一位的数值。

这种设计使得函数更加灵活和通用，能够适应不同的进制转换需求，而不仅仅是局限于十进制或八进制。