MoE
在讲这篇论文前先来说说什么是MoE
MoE是什么?
MoE,全称Mixture of Experts,混合专家模型。MoE是大模型架构的一种,其核心工作设计思路是“术业有专攻”,即将任务分门别类,然后分给多个“专家”进行解决。与MoE相对应的概念是稠密(Dense)模型,可以理解为它是一个“通才”模型。一个通才能够处理多个不同的任务,但一群专家能够更高效、更专业地解决多个问题。
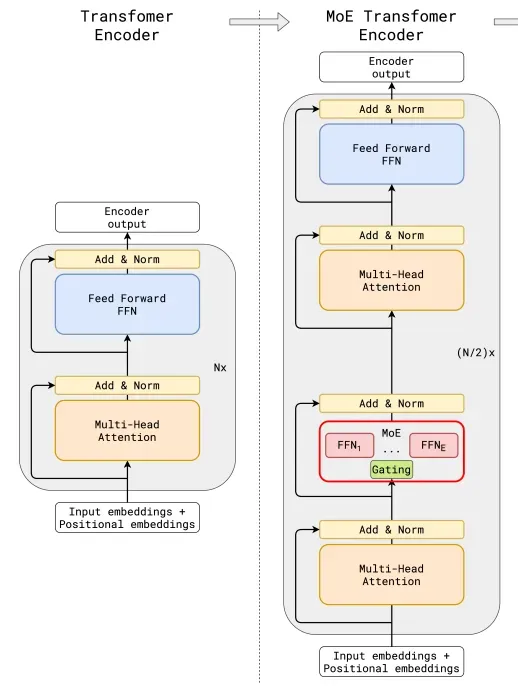
上图中,左侧图为传统大模型架构,右图为MoE大模型架构。两图对比可以看到,与传统大模型架构相比,MoE架构在数据流转过程中集成了一个专家网络层(红框部分)。下图为红框内容的放大展示:
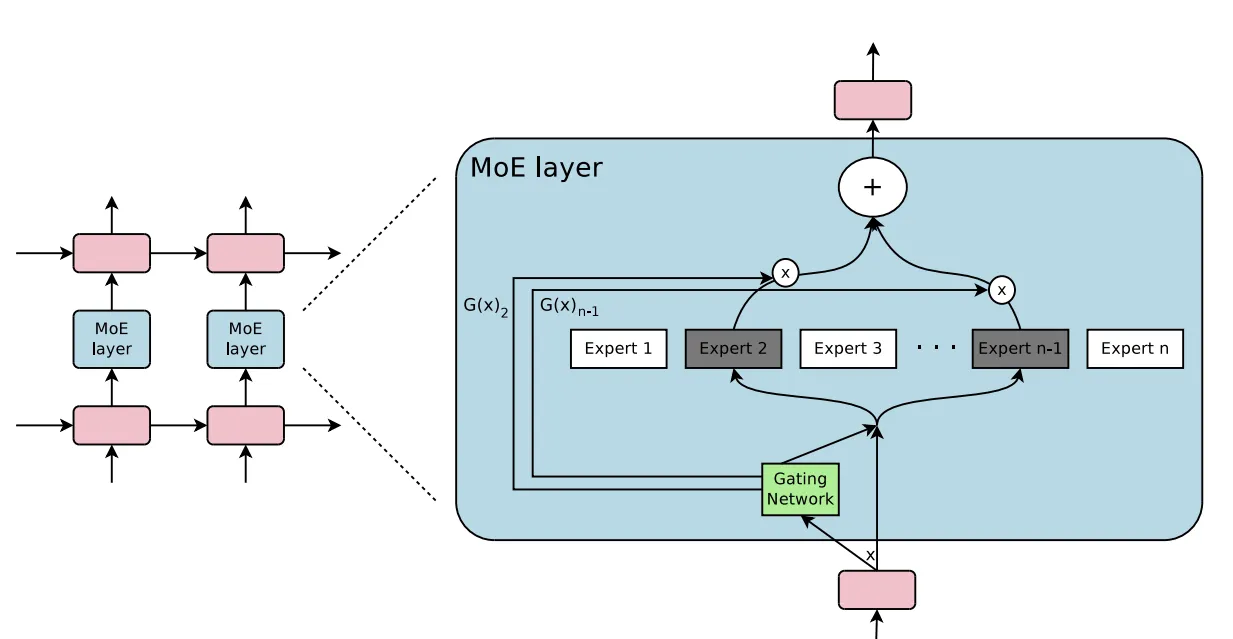
MoE如何设计的?
MoE架构的核心思想是将一个复杂的问题分解成多个更小、更易于管理的子问题,并由不同的专家网络分别处理。这些专家网络专注于解决特定类型的问题,通过组合各自的输出来提供最终的解决方案,提高模型的整体性能和效率。
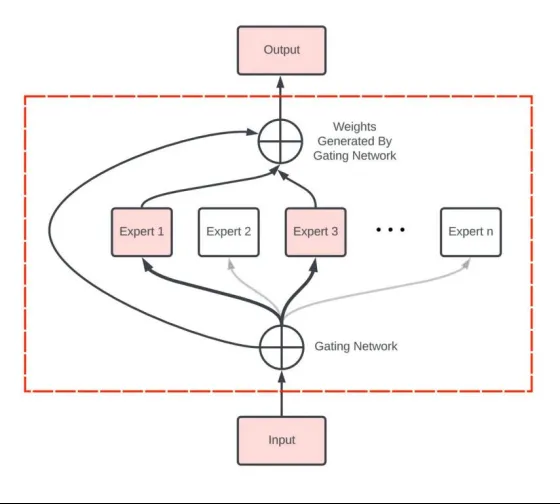
- 专家模型的选择与训练:
每个专家模型通常是针对特定任务或特定数据进行训练的。这些专家模型可以是不同的神经网络,分别在不同的数据集上进行优化,以便在特定领域内具有更好的性能。
在训练过程中,专家模型的选择可以基于特定的任务需求或数据特征。例如,可以有专门处理代码数据的专家模型,或者有处理科学论文的专家模型。
2. 门控机制(Gating Mechanism):
混合专家模型的核心在于门控机制,它负责在推理过程中动态选择和组合不同的专家模型。门控机制根据输入数据的特征,决定哪些专家模型对当前任务最有效。
常见的门控机制包括软门控(Soft Gating)和硬门控(Hard Gating)。软门控会为每个专家分配一个概率权重,所有专家的输出按照这些权重进行加权平均;硬门控则直接选择一个或几个专家进行输出。
3. 专家模型的组合与输出:
在推理阶段,混合专家模型会根据门控机制的选择,将多个专家模型的输出进行组合,以生成最终的结果。
这种组合可以是简单的加权求和,也可以是更复杂的融合策略,具体取决于任务的要求和门控机制的设计。
4. 优化与训练策略:
为了有效训练混合专家模型,通常需要设计特定的优化策略。例如,可以使用分阶段训练的方法,先分别训练每个专家模型,然后在整体框架中进行联合优化。
训练过程中还需要考虑专家模型之间的协同和竞争关系,确保每个专家模型能够在其擅长的领域内充分发挥作用,同时避免不必要的冗余和冲突。
MOE vs. Dense
MoE(专家混合模型)和Dense(稠密)模型在多个方面存在差异,以下是一些关键点:
| 指标 | MOE | Dense |
|---|---|---|
| 模型结构 | 模型由多个专家组成,每次计算时只有一部分专家被激活,从而减少了计算量。 | 所有参数和激活单元都参与每一次前向和后向传播计算。 |
| 计算效率 | 由于只激活部分专家,计算量和内存需求较少,因此在处理并发查询时具有更高的吞吐量。 | 计算量和内存需求随参数规模线性增长。 |
| 性能 | 可以在保持高效计算的同时,达到与大型Dense模型相似的性能。例如,50B的MoE模型理论性能接近34B的Dense模型。 | 性能稳定,但需要大量计算资源。 |
| 时延 | 由于只需加载和激活的专家,时延较低,尤其是在并发性较低的情况下。 | 由于需要加载所有参数,时延较高。 |
| 应用场景 | 适用于需要高效处理并发查询的任务,如大规模在线服务。 | 适用于需要稳定性能且计算资源充足的任务。 |
综上,MoE相对于Dense模型有以下几个优势:
吞吐量更高:MoE模型的激活单元少于密集层,因此在处理许多并发查询时,MoE模型具有更高的吞吐量。
时延更低:当并发性较低时,大部分时间用于将两个激活的专家模型加载到内存中,这比密集层需要的内存访问时间更少,从而降低了时延。
更高效的计算:对于单个查询,MoE需要从内存中读取的参数更少,因此在计算效率上优于密集层。
性能优越:MoE模型可以在保持小型模型的计算效率的同时,提供接近大型密集模型的强大性能。例如,Mistral MoE模型展示了在降低成本的同时,取得与更大模型相当的性能。
灵活性:可以将一个已经训练好的大型密集模型转换为MoE模型,使其具有小型模型的高效计算和大型密集模型的强大性能。
Mixtral of Experts
Mixtral of Experts 论文是由Mistral AI开源的,主要提出了一种新的专家模型(MoE)结构,该模型通过引入一种混合机制来改进当前MoE模型在性能、效率和适应性方面的不足。这种新的结构在处理并行任务和大规模模型时具有更高的灵活性和计算效率。
摘要
我们介绍了 Mixtral 8x7B,一种稀疏专家混合模型(Sparse Mixture of Experts,SMoE)语言模型。Mixtral 的架构与 Mistral 7B 相同,不同之处在于每一层由 8 个前馈块(即专家)组成。对于每个 token,在每一层中,路由网络会选择两个专家来处理当前状态并结合它们的输出。尽管每个 token 仅会接触到两个专家,但每个时间步选择的专家可以不同。因此,每个 token 可以访问到 470 亿个参数,但在推理过程中仅使用了 130 亿个活跃参数。Mixtral 的训练上下文长度为 32k tokens,并且在所有评估基准中表现优于或相当于 Llama 2 70B 和 GPT-3.5。特别是在数学、代码生成和多语言基准上,Mixtral 远超 Llama 2 70B。我们还提供了一个微调以便于指令跟随的模型 Mixtral 8x7B – Instruct,在人类基准测试中超越了 GPT-3.5 Turbo、Claude-2.1、Gemini Pro 和 Llama 2 70B – chat 模型。基础模型和指令微调模型都在 Apache 2.0 许可下发布。
可以看出,Mixtral 8x7B模型使用的是硬门控机制
介绍
在本文中,我们提出了 Mixtral 8x7B,一种具有开源权重的稀疏专家混合模型(Sparse Mixture of Experts,SMoE),并基于 Apache 2.0 许可发布。Mixtral 在大多数基准测试中优于 Llama 2 70B 和 GPT-3.5。由于它对每个 token 仅使用一部分参数,Mixtral 能够在小批量推理中实现更快的速度,并在大批量推理中提高吞吐量。
Mixtral 是一个稀疏的专家混合网络,是一种仅解码器模型,其中前馈块从 8 个不同的参数组中进行选择。在每一层,对于每个 token,路由网络会选择其中的两个组(即“专家”)来处理该 token,并通过加法结合它们的输出。这一技术增加了模型的参数数量,同时控制了计算成本和延迟,因为模型在每个 token 上仅使用了总参数的一部分。
Mixtral 使用多语言数据进行预训练,支持最大 32k tokens 的上下文长度。在多个基准测试中,它的表现达到或超越了 Llama 2 70B 和 GPT-3.5。特别是在数学、代码生成以及需要多语言理解的任务中,Mixtral 显著优于 Llama 2 70B。实验表明,Mixtral 能够从 32k tokens 的上下文窗口中成功检索信息,无论信息在序列中的长度或位置如何。
我们还介绍了 Mixtral 8x7B – Instruct,一个通过监督微调和直接偏好优化(Direct Preference Optimization)来微调的聊天模型,专门用于跟随指令。该模型在人类评估基准测试中显著超越了 GPT-3.5 Turbo、Claude-2.1、Gemini Pro 和 Llama 2 70B – chat 模型。此外,Mixtral – Instruct 在 BBQ 和 BOLD 等基准测试中展现出更低的偏见和更均衡的情感表现。
我们将 Mixtral 8x7B 和 Mixtral 8x7B – Instruct 在 Apache 2.0 许可下发布,可供学术和商业用途,确保广泛的可访问性和多样化应用的潜力。为了让社区能够使用完全开源的技术栈运行 Mixtral,我们向 vLLM 项目提交了更改,整合了用于高效推理的 Megablocks CUDA 内核。Skypilot 还支持在任何云实例上部署 vLLM 端点。
架构细节
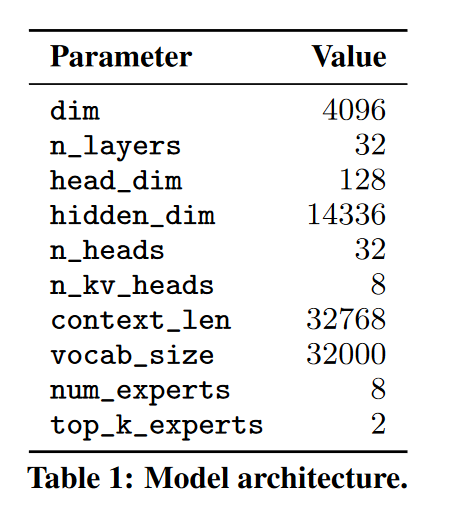
Mixtral 基于 Transformer 架构,并使用了相同的修改,主要区别在于 Mixtral 支持 32k tokens 的全稠密上下文长度,并将前馈块替换为专家混合层(第 2.1 节)。模型架构的参数总结见表 1。
稀疏专家混合模型
我们简要概述一下专家混合层(见图1)。对于给定的输入 x x x,MoE 模块的输出由各专家网络输出的加权和决定,其中权重由门控网络的输出提供。即,给定 n n n 个专家网络 { E 0 , E i , … , E n − 1 } \{E_0, E_i, \dots, E_{n-1}\} {E0,Ei,…,En−1},专家层的输出表示为:
Output = ∑ i = 0 n − 1 G ( x ) i ⋅ E i ( x ) \text{Output} = \sum_{i=0}^{n-1} G(x)_i \cdot E_i(x) Output=i=0∑n−1G(x)i⋅Ei(x)
这里, G ( x ) i G(x)_i G(x)i 表示第 i i i 个专家的门控网络的 n n n 维输出,而 E i ( x ) E_i(x) Ei(x) 是第 i i i 个专家网络的输出。如果门控向量是稀疏的,我们可以避免计算那些门值为零的专家的输出。实现 G ( x ) G(x) G(x) 有多种方式,一种简单且高效的方法是对线性层的 Top-K logits 取 softmax。我们使用以下公式:
G ( x ) : = Softmax ( TopK ( x ⋅ W g ) ) , G(x) := \text{Softmax}(\text{TopK}(x \cdot W_g)), G(x):=Softmax(TopK(x⋅Wg)),
其中, ( TopK ( ℓ ) ) i : = ℓ i (\text{TopK}(\ell))_i := \ell_i (TopK(ℓ))i:=ℓi 如果 ℓ i \ell_i ℓi 属于 logits ℓ ∈ R n \ell \in \mathbb{R}^n ℓ∈Rn 的前 K 个坐标,否则 ( TopK ( ℓ ) ) i : = − ∞ (\text{TopK}(\ell))_i := -\infty (TopK(ℓ))i:=−∞。
参数 K(即每个 token 使用的专家数量)是一个超参数,调节了每个 token 的计算量。如果在保持 K 不变的情况下增加 n n n,则可以增加模型的参数数量,同时有效地保持计算成本不变。
这引出了模型的总参数量(通常称为稀疏参数量)和用于处理单个 token 的参数数量(称为活跃参数量)之间的区别。稀疏参数量随 n n n 增长,而活跃参数量随 K K K 增长,最大可达 n n n。
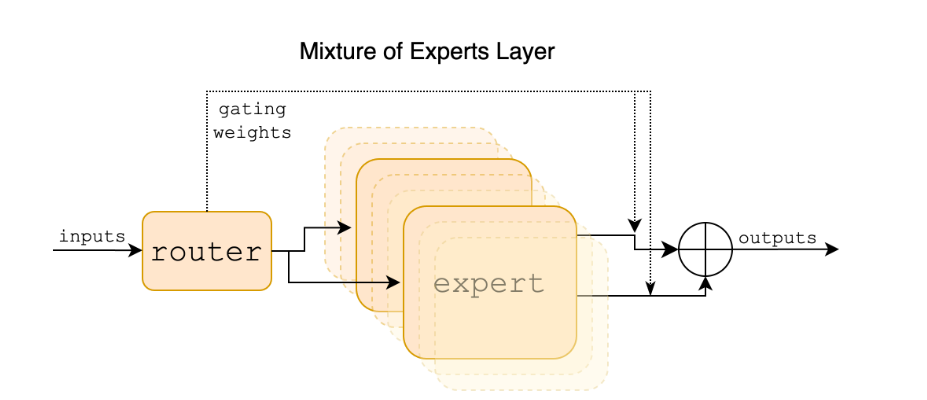
图 1:专家层混合。每个输入向量由路由器分配给 8 个专家中的 2 个。该层的输出是两个选定专家输出的加权和。在 Mixtral 中,专家是标准前馈块,就像普通Transformers架构中一样。
MoE 层可以通过高性能的专用内核在单个 GPU 上高效运行。例如,Megablocks 将 MoE 层的前馈网络(FFN)操作转换为大型稀疏矩阵乘法,显著提升了执行速度,并且可以自然地处理不同专家分配不同数量 token 的情况。此外,MoE 层可以通过标准的模型并行技术分布到多个 GPU 上,并通过一种称为专家并行(Expert Parallelism, EP)的特定分区策略实现。在 MoE 层的执行过程中,需要由特定专家处理的 token 被路由到相应的 GPU 进行处理,随后该专家的输出返回到原始 token 的位置。需要注意的是,EP 引入了负载均衡的挑战,因为将工作负载均匀分配到各 GPU 上是至关重要的,以防止个别 GPU 过载或出现计算瓶颈。
在 Transformer 模型中,MoE 层是针对每个 token 独立应用的,并替代了 Transformer 块中的前馈(FFN)子块。对于 Mixtral,我们使用相同的 SwiGLU 架构作为专家函数 E i ( x ) E_i(x) Ei(x),并设定 K = 2 K = 2 K=2。 这意味着每个 token 被路由到两个具有不同权重的 SwiGLU 子块。结合以上所有内容,对于输入 token x x x 的输出 y y y 计算如下:
y = ∑ i = 0 n − 1 Softmax ( Top2 ( x ⋅ W g ) ) i ⋅ SwiGLU i ( x ) 。 y = \sum_{i=0}^{n-1} \text{Softmax}(\text{Top2}(x \cdot W_g))_i \cdot \text{SwiGLU}_i(x)。 y=i=0∑n−1Softmax(Top2(x⋅Wg))i⋅SwiGLUi(x)。
SwiGLU(Swish-Gated Linear Units)是一种激活函数,用于改进深度学习模型中的前馈网络(FFN)结构。它最初是在 Google 的 Switch Transformer 论文中提出的,旨在提高模型的非线性表达能力,从而提升模型的性能和效率。
其计算公式如下:
SwiGLU ( x ) = ( swish ( x 1 ) ⊙ x 2 ) = ( sigmoid ( x 1 ) ⋅ x 1 ) ⊙ x 2 \text{SwiGLU}(x) = (\text{swish}(x_1) \odot x_2) = (\text{sigmoid}(x_1) \cdot x_1) \odot x_2 SwiGLU(x)=(swish(x1)⊙x2)=(sigmoid(x1)⋅x1)⊙x2
其中:
x 1 x_1 x1和 x 2 x_2 x2是通过不同的线性变换获得的输入张量。在 SwiGLU 中,输入 x x x经过两个不同的线性变换生成 x 1 x_1 x1和 x 2 x_2 x2。首先进行线性变换:对输入 x x x 进行两个不同的线性投影,生成 x 1 x_1 x1 和 x 2 x_2 x2。这可以表示为:
x 1 = W 1 ⋅ x + b 1 x_1 = W_1 \cdot x + b_1 x1=W1⋅x+b1
x 2 = W 2 ⋅ x + b 2 x_2 = W_2 \cdot x + b_2 x2=W2⋅x+b2
其中 W 1 W_1 W1 和 W 2 W_2 W2 是两个不同的权重矩阵, b 1 b_1 b1 和 b 2 b_2 b2 是对应的偏置向量。
⊙ \odot ⊙表示元素级别的乘法操作。Swish 激活函数的公式是 swish ( x ) = x ⋅ sigmoid ( x ) \text{swish}(x) = x \cdot \text{sigmoid}(x) swish(x)=x⋅sigmoid(x),其中 sigmoid ( x ) = 1 1 + e − x \text{sigmoid}(x) = \frac{1}{1 + e^{-x}} sigmoid(x)=1+e−x1。
结果
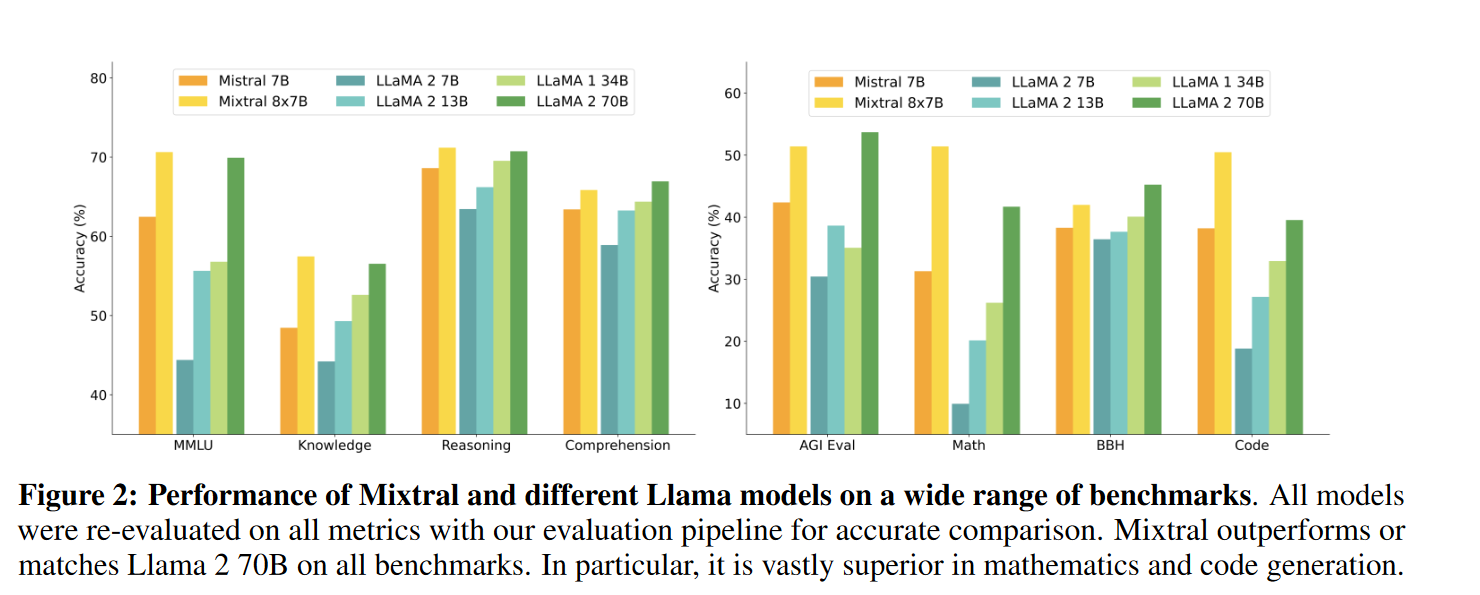
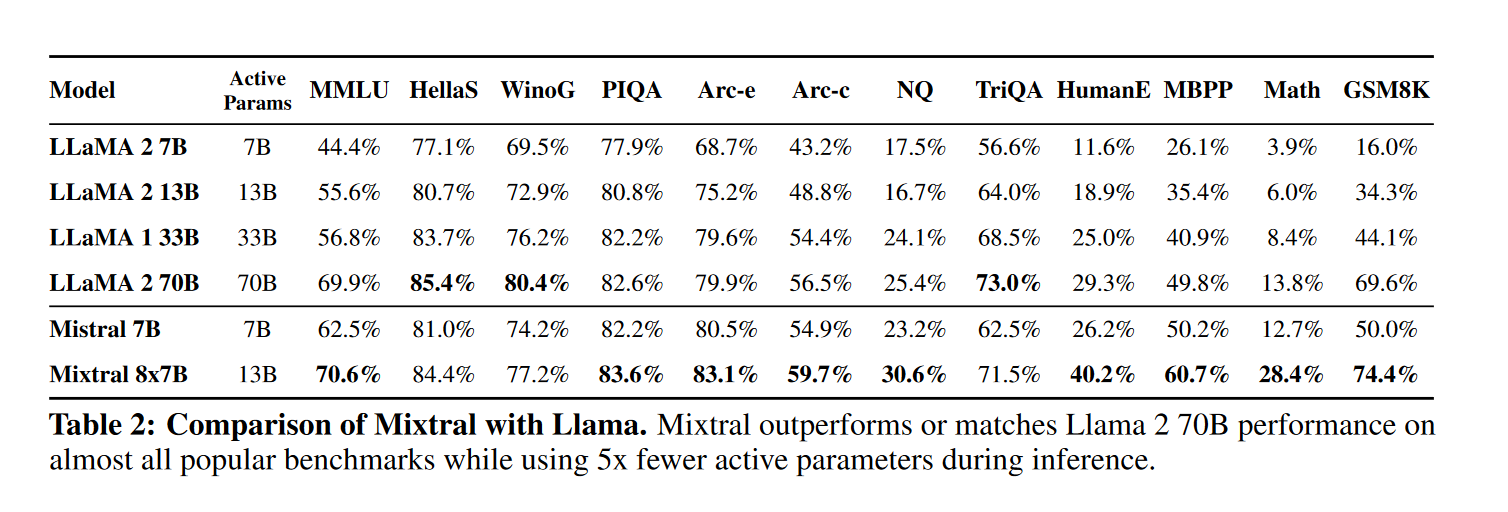
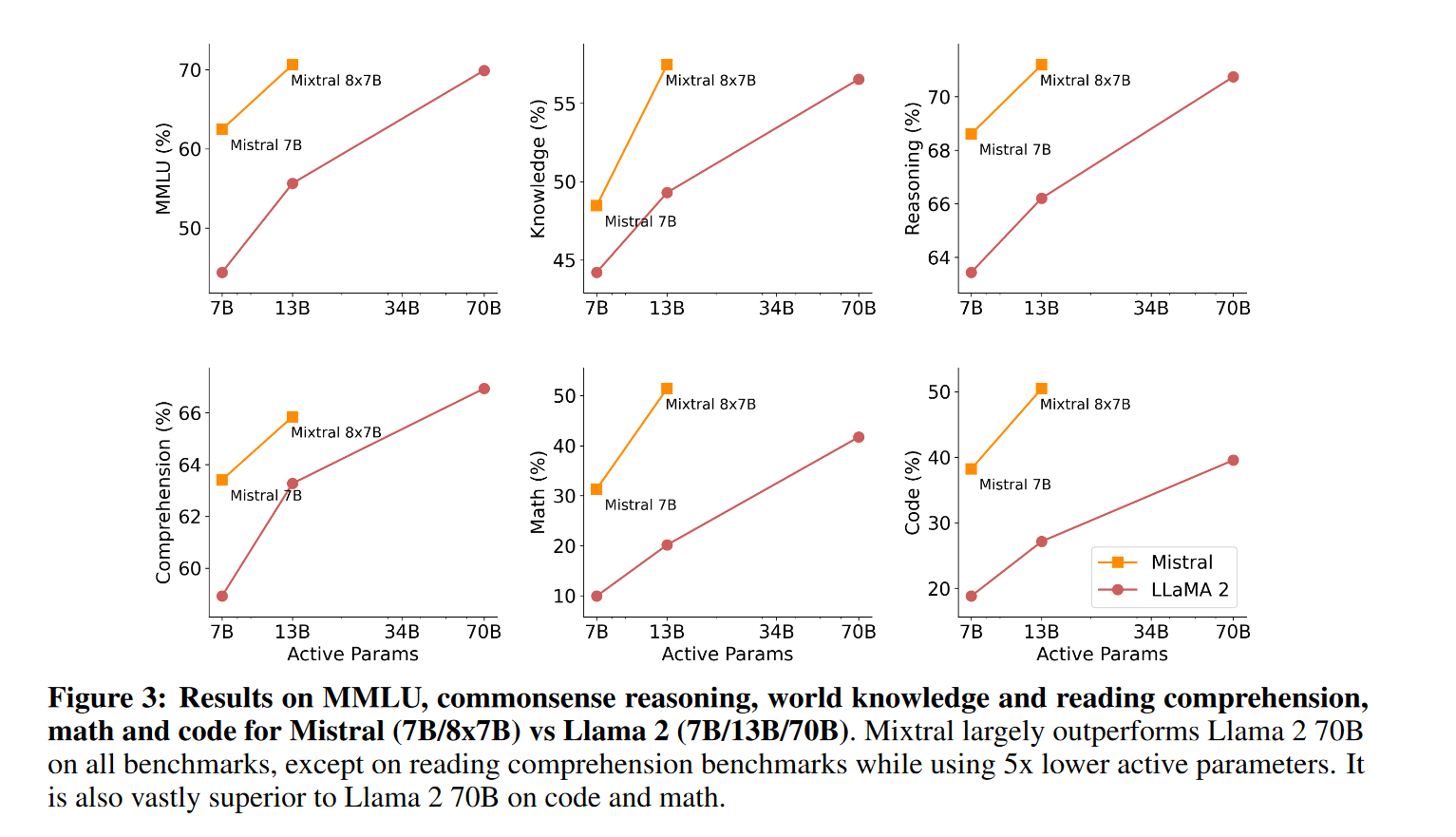
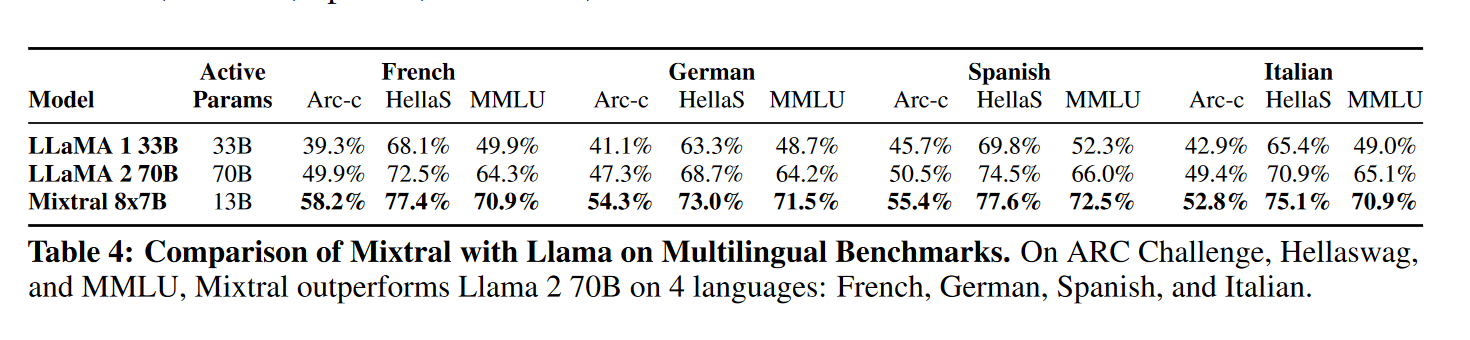
我将论文中的一些结果放在这里,展示了Mistral 8*7B的效果比LLaMA2好
- 常识推理(0-shot):Hellaswag、Winogrande、PIQA、SIQA、OpenbookQA、ARC-Easy、ARC-Challenge、CommonsenseQA
- 世界知识(5-shot):NaturalQuestions、TriviaQA
- 阅读理解(0-shot):BoolQ、QuAC
- 数学:GSM8K(8-shot,使用 maj@8)和 MATH(4-shot,使用 maj@4)
- 代码:Humaneval(0-shot)和 MBPP(3-shot)
- 流行的综合结果:MMLU(5-shot)、BBH(3-shot)、AGI Eval(3-5-shot,仅限英语选择题)
指令微调
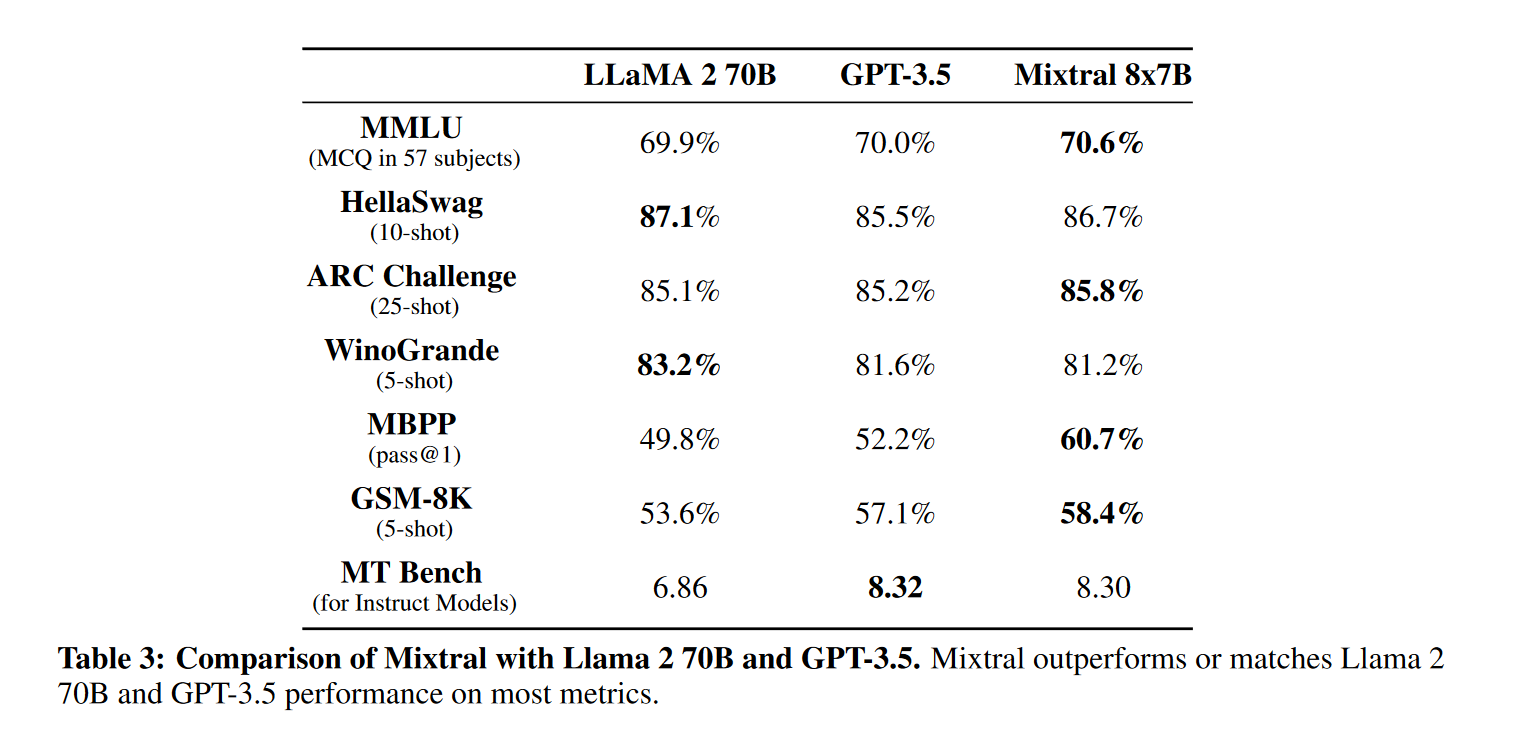
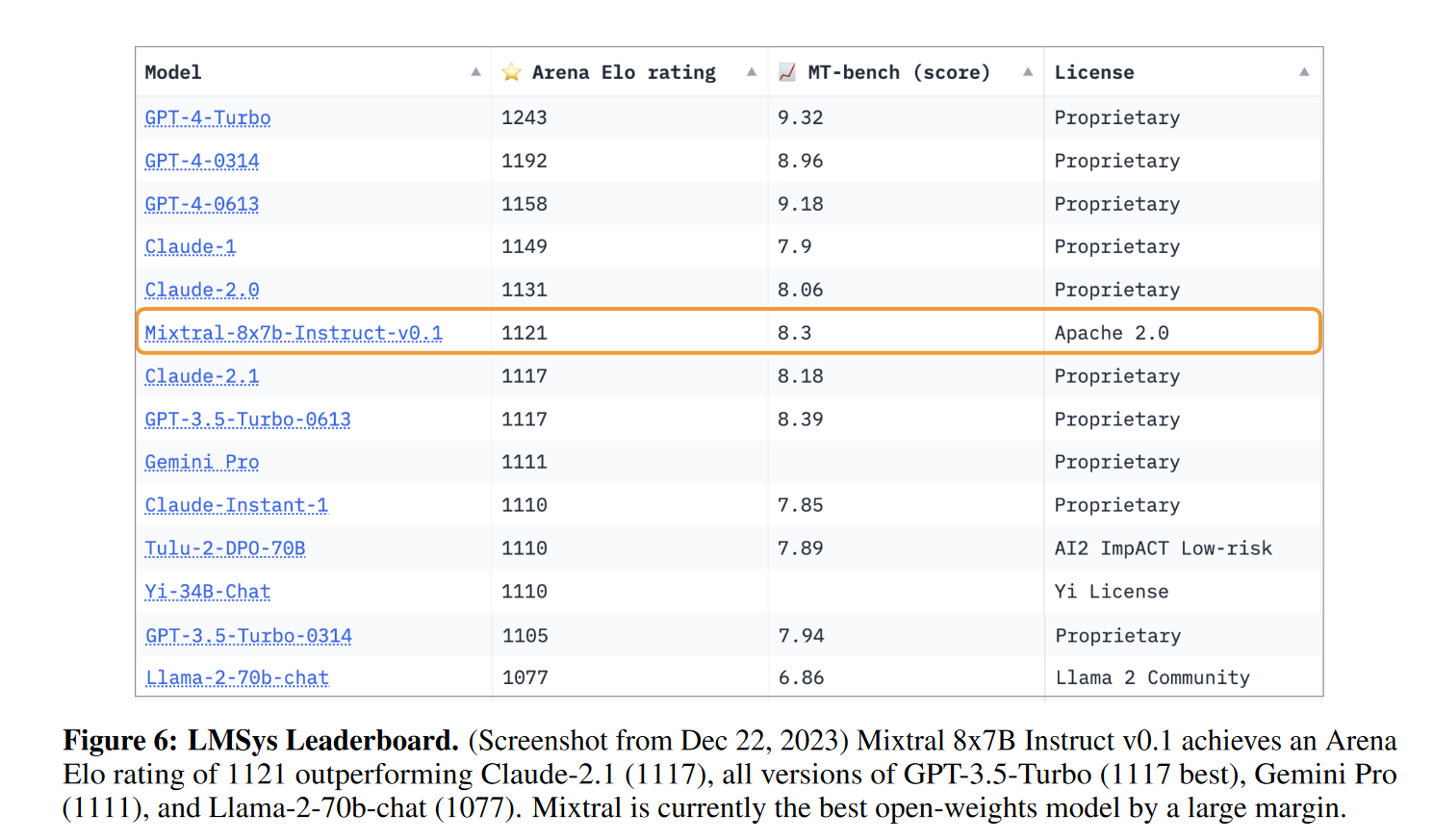
通过在指令数据集上进行监督微调(SFT),然后在配对反馈数据集上进行直接偏好优化(DPO)来训练 Mixtral – Instruct。Mixtral – Instruct 在 MT-Bench 上达到了 8.30 分(见表 2),使其成为截至 2023 年 12 月最佳的开源权重模型。由 LMSys 进行的独立人工评估结果显示,Mixtral – Instruct 的表现优于 GPT-3.5-Turbo、Gemini Pro、Claude-2.1 和 Llama 2 70B chat。
路由分析
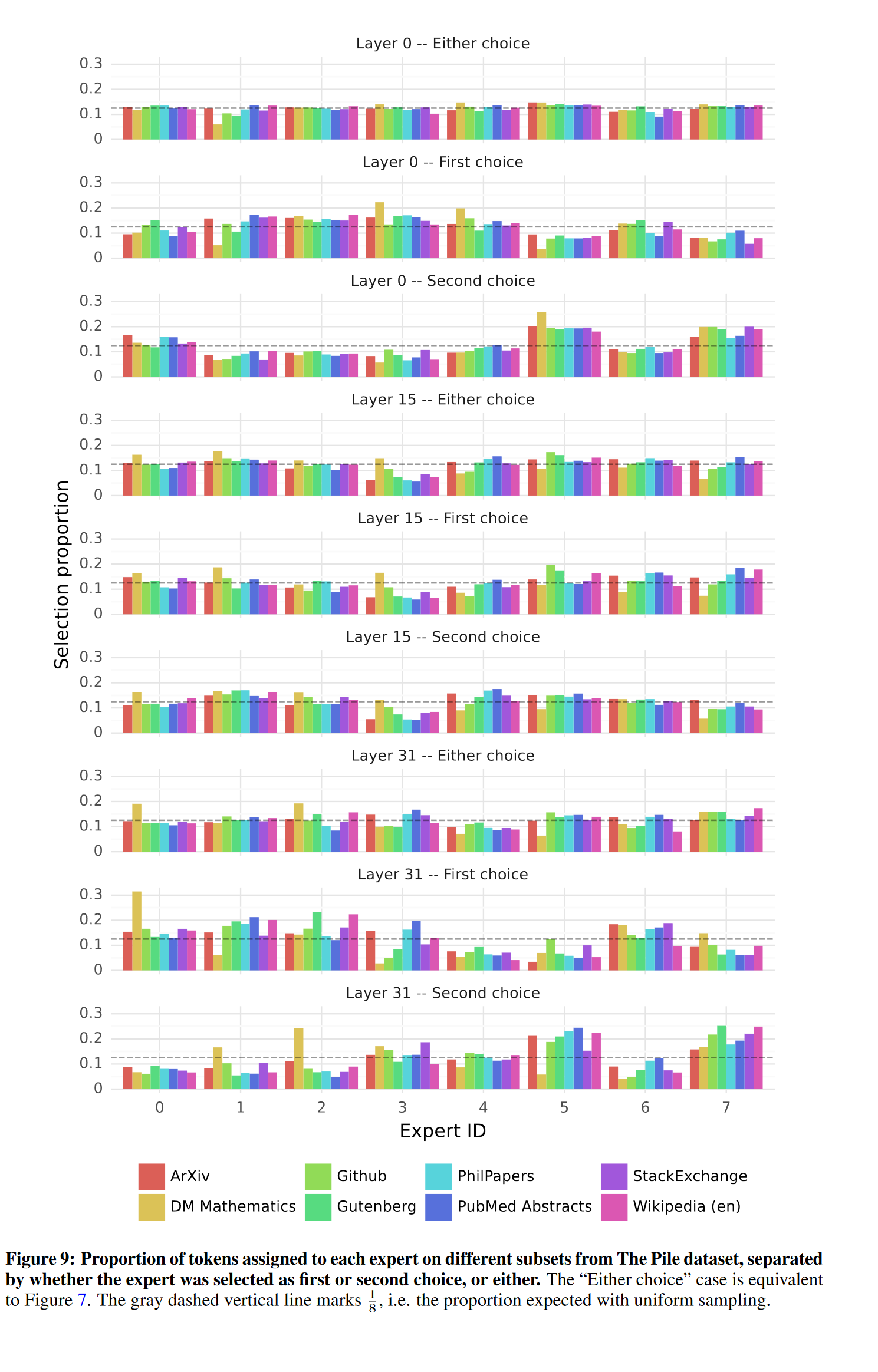
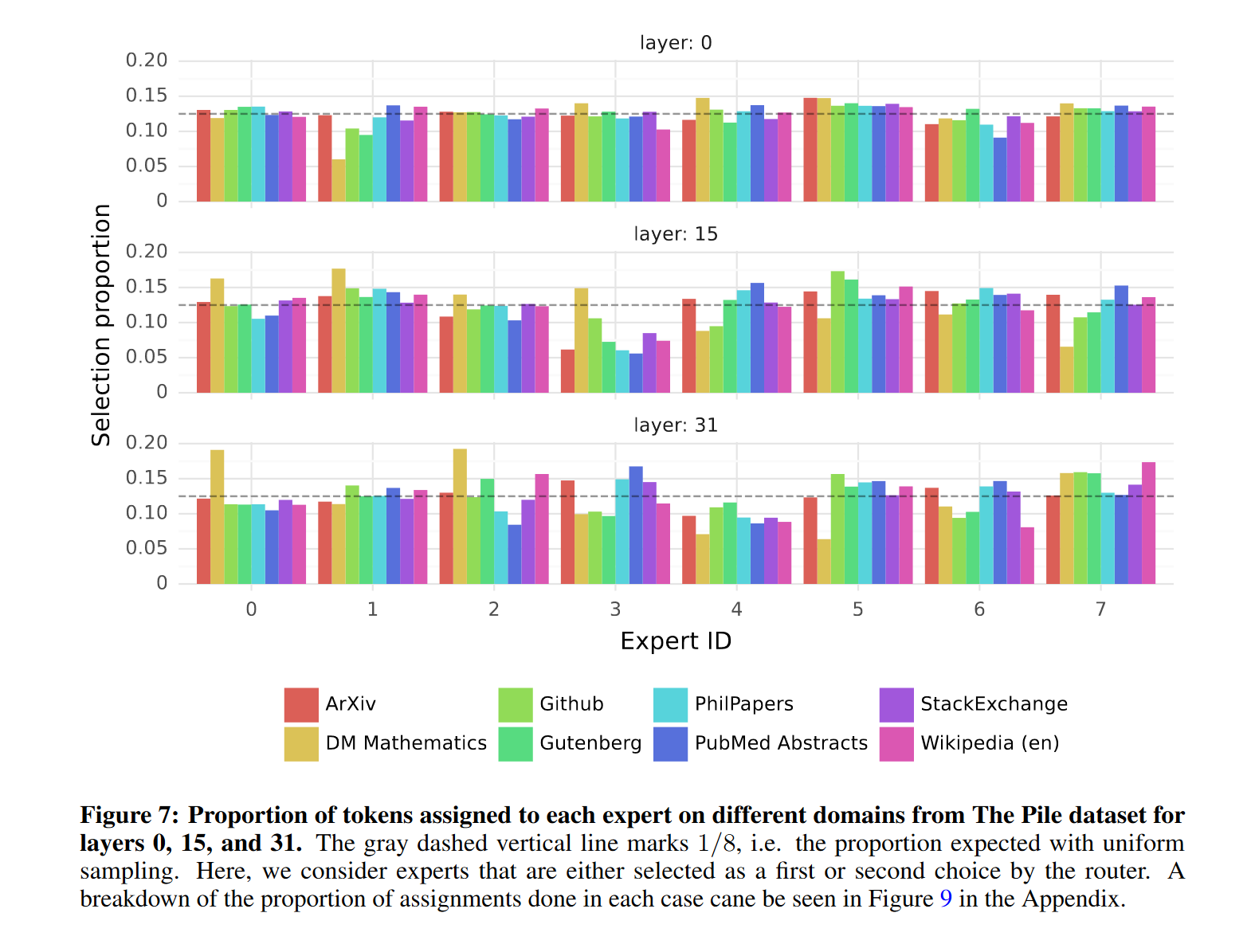
在本节中,我们对路由器选择专家的情况进行了一些小规模分析。特别地,我们希望了解在训练过程中,某些专家是否专门化于特定领域(例如数学、生物学、哲学等)。为此,我们测量了不同子集上选定专家的分布情况,这些子集来自 The Pile 验证数据集。图 7 展示了第 0 层、第 15 层和第 31 层的结果(第 0 层和第 31 层分别是模型的第一层和最后一层)。令人惊讶的是,我们没有观察到基于主题的专家分配的明显模式。例如,在所有层中,对于 ArXiv 论文(用 LaTeX 编写)、生物学(PubMed 摘要)和哲学(PhilPapers)文档,专家分配的分布非常相似。只有在 DM 数学数据集中,我们观察到略有不同的专家分布。这种差异可能是由于数据集的合成性质以及它对自然语言覆盖范围有限,尤其在模型的第一层和最后一层更加明显,因为这些层的隐藏状态分别与输入和输出嵌入高度相关。这表明路由器确实表现出某种结构化的句法行为。
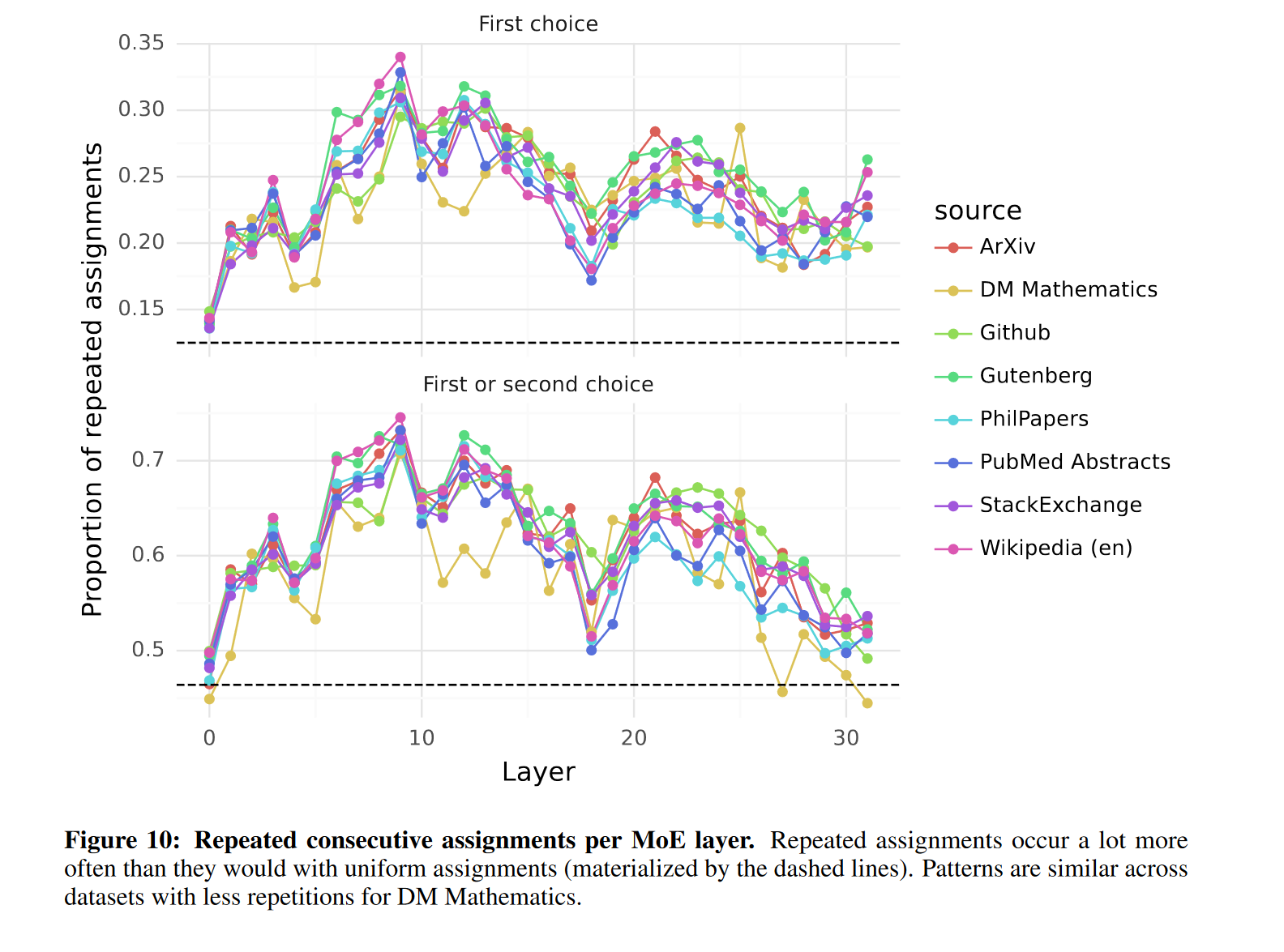
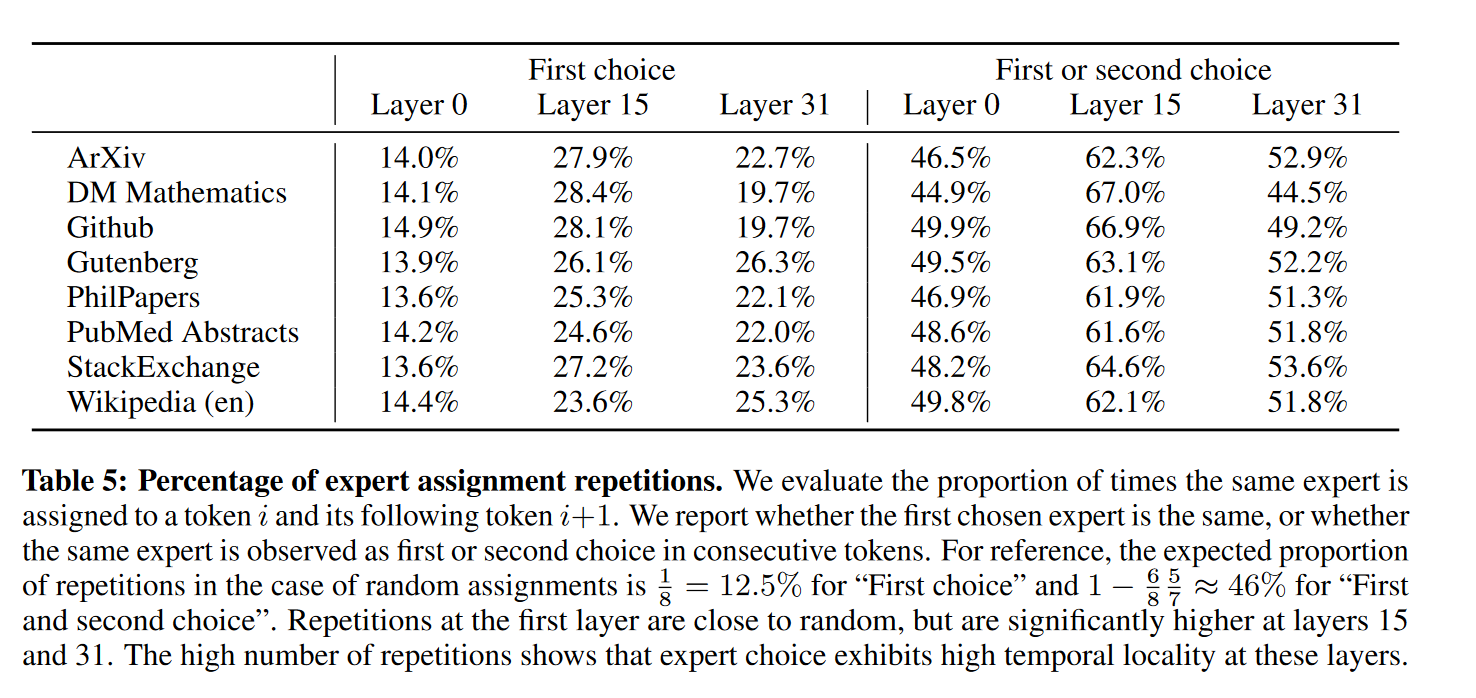
图 8 显示了来自不同领域的文本示例(Python 代码、数学和英语),其中每个 token 根据其选定的专家被标记为不同的背景颜色。该图表明,即使涉及多个 token,像 Python 中的 “self” 和英语中的 “Question” 这样的词汇也常常通过相同的专家进行路由。类似地,在代码中,缩进 token 在第一层和最后一层始终被分配给相同的专家,因为这些层的隐藏状态与模型的输入和输出更相关。此外,我们还从图 8 中注意到,连续的 token 通常会被分配给相同的专家。事实上,我们在 The Pile 数据集中观察到了一定程度的位置局部性。表 5 显示了每个领域和层中连续 token 获得相同专家分配的比例。在较高层中,连续分配相同专家的比例显著高于随机分配。这对模型的快速训练和推理优化有一定影响。例如,在进行专家并行时,高局部性的情况更可能导致某些专家的过度订阅。相反,这种局部性可以用于缓存,如某些技术所实现的那样。
附录图 10 提供了所有层和各数据集上相同专家频率的更完整视图。

附录