7.链表
7.1相交链表(简单)
题目描述:leetcode链接 160.相交链表
给你两个单链表的头节点
headA和headB,请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点,返回null。图示两个链表在节点
c1开始相交:
题目数据 保证 整个链式结构中不存在环。
注意,函数返回结果后,链表必须 保持其原始结构 。
自定义评测:
评测系统 的输入如下(你设计的程序 不适用 此输入):
intersectVal- 相交的起始节点的值。如果不存在相交节点,这一值为0listA- 第一个链表listB- 第二个链表skipA- 在listA中(从头节点开始)跳到交叉节点的节点数skipB- 在listB中(从头节点开始)跳到交叉节点的节点数评测系统将根据这些输入创建链式数据结构,并将两个头节点
headA和headB传递给你的程序。如果程序能够正确返回相交节点,那么你的解决方案将被 视作正确答案 。
示例 1:
输入:intersectVal = 8, listA = [4,1,8,4,5], listB = [5,6,1,8,4,5], skipA = 2, skipB = 3 输出:Intersected at '8' 解释:相交节点的值为 8 (注意,如果两个链表相交则不能为 0)。 从各自的表头开始算起,链表 A 为 [4,1,8,4,5],链表 B 为 [5,6,1,8,4,5]。 在 A 中,相交节点前有 2 个节点;在 B 中,相交节点前有 3 个节点。 — 请注意相交节点的值不为 1,因为在链表 A 和链表 B 之中值为 1 的节点 (A 中第二个节点和 B 中第三个节点) 是不同的节点。换句话说,它们在内存中指向两个不同的位置,而链表 A 和链表 B 中值为 8 的节点 (A 中第三个节点,B 中第四个节点) 在内存中指向相同的位置。
示例 2:
输入:intersectVal = 2, listA = [1,9,1,2,4], listB = [3,2,4], skipA = 3, skipB = 1 输出:Intersected at '2' 解释:相交节点的值为 2 (注意,如果两个链表相交则不能为 0)。 从各自的表头开始算起,链表 A 为 [1,9,1,2,4],链表 B 为 [3,2,4]。 在 A 中,相交节点前有 3 个节点;在 B 中,相交节点前有 1 个节点。示例 3:
输入:intersectVal = 0, listA = [2,6,4], listB = [1,5], skipA = 3, skipB = 2 输出:No intersection 解释:从各自的表头开始算起,链表 A 为 [2,6,4],链表 B 为 [1,5]。 由于这两个链表不相交,所以 intersectVal 必须为 0,而 skipA 和 skipB 可以是任意值。 这两个链表不相交,因此返回 null 。
思路:
1.两个链表的头节点分别为headA和headB
2.令ListNode* A = headA,ListNode* B = headB
3.判断A、B是否相等
如果A != nullptr,则A = A -> next,否则A = headB;
如果B != nullptr,则B = B -> next,否则B = headA;
4.具体的遍历顺序如图所示,其中粉红色箭头是A的遍历顺序,绿色箭头是B的遍历顺序

举例说明:
见上图
若两链表不相交,则遍历完成后,A、B均为nullptr,return A即可
代码:
class Solution {
public:ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {ListNode* A = headA;ListNode* B = headB;while (A != B) {A = A != nullptr ? A -> next : headB;B = B != nullptr ? B -> next : headA;}return A;}
};7.2反转链表(简单)
题目描述:leetcode链接 206. 反转链表
给你单链表的头节点
head,请你反转链表,并返回反转后的链表。示例 1:
输入:head = [1,2,3,4,5] 输出:[5,4,3,2,1]示例 2:
输入:head = [1,2] 输出:[2,1]示例 3:
输入:head = [] 输出:[]
思路:


举例说明:
以上图为例,最后返回pre即可
代码:
class Solution {
public:ListNode* reverseList(ListNode* head) {ListNode* cur = head;ListNode* pre = nullptr;while (cur) {ListNode* temp = cur -> next;cur -> next = pre;pre = cur;cur = temp;}return pre;}
};7.3回文链表(简单)
题目描述:leetcode链接 234. 回文链表
给你一个单链表的头节点
head,请你判断该链表是否为回文链表
。如果是,返回true;否则,返回false。示例 1:
输入:head = [1,2,2,1] 输出:true示例 2:
输入:head = [1,2] 输出:false
思路:
将链表内每个节点的值存储到vectot<int> res中,从res的两端向中间遍历,比较它们的值

举例说明:
如上图所示
代码:
class Solution {
public:bool isPalindrome(ListNode* head) {vector<int> res;ListNode* cur = head;while (cur) {res.push_back(cur -> val);cur = cur -> next;}for (int i = 0, j = res.size() - 1; i < j; i++, j--) {if (res[i] != res[j]) return false;}return true;}
};7.4环形链表(简单)
题目描述:leetcode链接 141. 环形链表
给你一个链表的头节点
head,判断链表中是否有环。如果链表中有某个节点,可以通过连续跟踪
next指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数pos来表示链表尾连接到链表中的位置(索引从 0 开始)。注意:pos不作为参数进行传递 。仅仅是为了标识链表的实际情况。如果链表中存在环 ,则返回
true。 否则,返回false。示例 1:
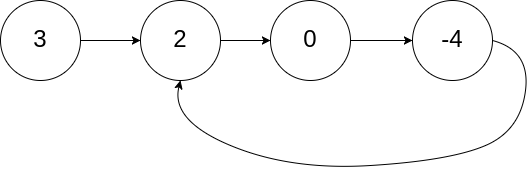
输入:head = [3,2,0,-4], pos = 1 输出:true 解释:链表中有一个环,其尾部连接到第二个节点。示例 2:
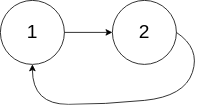
输入:head = [1,2], pos = 0 输出:true 解释:链表中有一个环,其尾部连接到第一个节点。示例 3:
输入:head = [1], pos = -1 输出:false 解释:链表中没有环。
思路:
1.使用快慢指针fast和slow,都从头指针head出发,fast每次走2步,slow每次走1步
2.由于fast相对于slow的相对速度为1,这意味着只要链表存在环,fast和slow最后一定会相遇
举例说明:

代码:
class Solution {
public:bool hasCycle(ListNode *head) {ListNode* fast = head;ListNode* slow = head;while (fast && fast -> next) {fast = fast -> next -> next;slow = slow -> next;if (fast == slow) return true;}return false;}
};7.5环形链表II(中等)
题目描述:leetcode链接 142. 环形链表 II
给定一个链表的头节点
head,返回链表开始入环的第一个节点。 如果链表无环,则返回null。如果链表中有某个节点,可以通过连续跟踪
next指针再次到达,则链表中存在环。 为了表示给定链表中的环,评测系统内部使用整数pos来表示链表尾连接到链表中的位置(索引从 0 开始)。如果pos是-1,则在该链表中没有环。注意:pos不作为参数进行传递,仅仅是为了标识链表的实际情况。不允许修改 链表。
示例 1:
输入:head = [3,2,0,-4], pos = 1 输出:返回索引为 1 的链表节点 解释:链表中有一个环,其尾部连接到第二个节点。示例 2:
输入:head = [1,2], pos = 0 输出:返回索引为 0 的链表节点 解释:链表中有一个环,其尾部连接到第一个节点。示例 3:
输入:head = [1], pos = -1 输出:返回 null 解释:链表中没有环。
思路:
leetcode l41.环形链表是判断链表是否存在环,本题则是需要寻找链表入环的第一个节点,相比leetcode l41.环形链表会需要多一些步骤才能实现。

假设fast和slow在相遇时分别走过的步数分别为f和s
s = a + b + m * (b + c)
f = a + b + (n + 2 * m) * (b + c)
可以看到,如果m>0,那么意味着在s = a + b 和 f = a + b + n * (b + c)时fast和slow就已经相遇了,所以m=0。即:
s = a + b
f = a + b + n * (b + c),其中n>=1
又由于f = 2 * s,所以 a + b + n * (b + c) = 2 * (a + b),a = c + (n - 1) * (b + c),也即当fast和slow相遇时,令ListNode* index1= head,ListNode* index2 = slow,当index1和index2走过a步之后,会相遇在环形链表的入口节点

举例说明:
见上图
代码:
class Solution {
public:ListNode *detectCycle(ListNode *head) {ListNode* fast = head;ListNode* slow = head;while (fast && fast -> next) {fast = fast -> next -> next;slow = slow -> next;if (fast == slow) {ListNode* index1 = head;ListNode* index2 = slow;while (index1 != index2) {index1 = index1 -> next;index2 = index2 -> next;}return index1;}}return nullptr;}
};