一、引入
“在一棵树上进行路径的修改、求极值、求和”乍一看只要线段树就能轻松解决,实际上,仅凭线段树是不能搞定它的。我们需要用到一种貌似高级的复杂算法——「树链剖分」。
树链剖分(简称树剖),顾名思义,将一棵树划分成若干条进行处理,分为「重链剖分」和「长链剖分」,通常会搭配数据结构使用(如树状数组、线段树、主席树等)。
因为重链剖分的应用多,所以树链剖分一般默认为重链剖分。
二、重链剖分
2.1 概念
-
重儿子 / 轻儿子:定义 s i z u siz_u sizu 表示以 u u u 为根的子树的大小。对于节点 u u u 而言,它的儿子中 s i z siz siz 最大的为重儿子,其余为轻儿子。(特别地,这里定义节点 u u u 的重儿子 / 轻儿子,前提是节点 u u u 为非叶子节点)
-
重边 / 轻边:令节点 u u u 的重儿子为 v v v,则 ( u , v ) (u,v) (u,v) 称作为重边,其余称作为轻边。
-
重链:由重边相连组成的链。
-
链首:每条链中深度最小的点(起点)。
-
对于叶子节点,若其为轻儿子,则有一条以自己为起点长度为 1 1 1 的链。
-
每一条重链以轻儿子为链首(起点)。
如下图所示(转载自洛谷日报「树链剖分」),较粗的为重边,较细的为轻边。节点编号旁边有个红色点的表明该节点是其所在链的链首。边旁的蓝色数字表示该边在线段树中的位置。
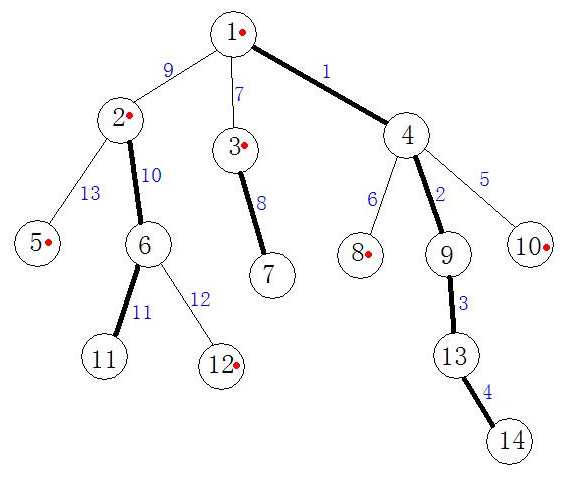
例如,图中 1 − 4 − 9 − 13 − 14 1-4-9-13-14 1−4−9−13−14 为一条重链。
2.2 算法实现
共需要做两次 dfs,先列出需要维护的信息:
-
fa[u],节点 u u u 的父亲,通常默认根节点为 1 1 1,且其父亲为 0 0 0。 -
dep[u],节点u的深度,通常默认根节点的深度为 1 1 1。 -
siz[u],以节点u为根的子树的大小。 -
hs[u],节点u的重儿子,若为叶子节点则赋值为-1。 -
top[u],节点u所在的重链的链首。 -
w[u],节点u在剖分完后的编号(DFS序)。 -
pos[u],节点u在线段树上的位置。
第一次 dfs 维护 fa[],dep[],siz[],hs[],注意初始化。
vector<int> g[N];//存边
void dfs1(int u,int fath)
{fa[u]=fath;dep[u]=dep[fath]+1;siz[u]=1;hs[u]=-1;for(auto v:g[u]){if(v==fath) continue;dfs1(v,u);siz[u]+=siz[v];if(hs[u]==-1||siz[v]>siz[hs[u]]) hs[u]=v;}
}
第二次 dfs 维护 top[],w[],pos[]。
void dfs2(int u,int t)
{top[u]=t;w[u]=++cnt;pos[cnt]=u;if(hs[u]!=-1) dfs2(hs[u],t);for(auto v:g[u])if(v!=fa[u]&&hs[u]!=v)dfs2(v,v);
}
顺带一提如果要套用线段树等,记得建树时加上pos[],如下:
#define ls u<<1
#define rs u<<1|1
void build(int u,int l,int r)
{if(l==r){t[u]=a[pos[l]];return;}int mid=(l+r)>>1;build(ls,l,mid);build(rs,mid+1,r);push_up(u);
}
主函数这么打就好了:
//前面读入存图略
dfs1(1,0);//这里默认 1 为根节点,根据题目不同可以改为不同的根节点(两次 dfs 所有的 1 都要改)
dfs2(1,1);
build(1,1,n);
2.3 性质
- 性质 1 1 1:若 v v v 是 u u u 的轻儿子,即轻边 ( u , v ) (u,v) (u,v),则一定有 s i z v ≤ s i z u 2 siz_v \leq \frac{siz_u}{2} sizv≤2sizu。
证明:显然,用反证法,假设 s i z v > s i z u 2 siz_v > \frac{siz_u}{2} sizv>2sizu,那么 v v v 就是 u u u 的重儿子,与 v v v 是 u u u 的轻儿子矛盾,故 s i z v ≤ s i z u 2 siz_v \leq \frac{siz_u}{2} sizv≤2sizu。
- 性质 2 2 2:节点 u u u 与节点 f a t o p u fa_{top_u} fatopu 一定不在同一条重链上。
证明:显然,用反证法,令 v = t o p [ u ] v=top[u] v=top[u],假设节点 v v v 与节点 f a v fa_v fav 在同一条链上,由于 v v v 是 u u u 所在重链的链首,故 ( f a v , v ) (fa_v,v) (fav,v) 是轻边,所以 v v v 与 f a v fa_v fav 不在同一条重链上,矛盾。
- 性质 3 3 3:从根节点到树上任意一点的路径上的轻边数不超过 log n \log{n} logn。
证明:由上一性质可知,从根节点向下走,每经过一条轻边,以到达的节点为根的子树的节点个数至少比以上一个节点为根的子树减少一半,因此从根节点到树上任意一点的路径上的轻边数不超过 log n \log{n} logn。
- 性质 4 4 4:从根节点到树上任意一点的路径上的重链数不超过 log n \log{n} logn。
证明:由上一性质可以,从根节点到树上任意一点的路径上的轻边数不超过 log n \log{n} logn。显然每一条重链的两端都是轻边,因此从根节点到树上任意一点的路径上的重链数不超过 log n \log{n} logn。
2.4 时间复杂度 & 应用
-
从根到任何一条链只需要经过 O ( log n ) O(\log{n}) O(logn) 条链,故每次操作的时间复杂度为 O ( log n ) O(\log{n}) O(logn)。
-
重链剖分使得每一条链上的 DFS 序是有序且连续的,这个特殊的性质对于解决一下树上问题十分的有利,也提供了一种新的方式求 LCA(最近公共祖先)。
树剖求 LCA:
不断向上跳重链,当跳到同一条重链上时,深度较小的结点即为 LCA。
int LCA(int u,int v)
{while(top[u]^top[v]){if(dep[top[u]]<dep[top[v]]) swap(u,v);//深度大的先往上跳u=fa[top[u]];}if(dep[u]<dep[v]) swap(u,v);return v;
}
2.5 例题讲解
例1. P3384 【模板】重链剖分/树链剖分
一道比较典型的树剖模板,也涵盖了一些操作的打法。
-
1 x y z,表示将树从 x x x 到 y y y 结点最短路径上所有节点的值都加上 z z z。 -
2 x y,表示求树从 x x x 到 y y y 结点最短路径上所有节点的值之和。 -
3 x z,表示将以 x x x 为根节点的子树内所有节点值都加上 z z z。 -
4 x,表示求以 x x x 为根节点的子树内所有节点值之和。
显然前两个操作属于路径上操作 / 询问,后两个操作属于以某一节点为根的子树上操作 /询问。
操作 1 1 1 与求 LCA 差不多,只不过多几步 update 罢了,对最短路 ( x , y ) (x,y) (x,y) 的操作,显然可以转换成 ( x , l c a ) (x,lca) (x,lca) 和 ( y , l c a ) (y,lca) (y,lca) 操作,这里用树剖的话直接跳重链即可:
void modify(int u,int v,ll k)
{while(top[u]^top[v]){if(dep[top[u]]<dep[top[v]]) swap(u,v);update(1,1,n,w[top[u]],w[u],k);u=fa[top[u]];}if(dep[u]<dep[v]) swap(u,v);update(1,1,n,w[v],w[u],k);
}
操作 2 2 2 改为求和即可:
ll query(int u,int v)
{ll ans=0;while(top[u]^top[v]){if(dep[top[u]]<dep[top[v]]) swap(u,v);ans=(ans+query(1,1,n,w[top[u]],w[u]))%p;u=fa[top[u]];}if(dep[u]<dep[v]) swap(u,v);ans=(ans+query(1,1,n,w[v],w[u]))%p;return ans;
}
因为树剖后树上的 DFS 序在一条链上有序且连续的,并且以某一节点为根的子树内也是一样的,故对于操作 3 3 3、 4 4 4,直接修改 / 询问 w [ u ] w[u] w[u] 到 w [ u ] + s i z [ u ] − 1 w[u]+siz[u]-1 w[u]+siz[u]−1 即可。
if(opt==3)
{scanf("%lld",&k);update(1,1,n,w[x],w[x]+siz[x]-1,k);
}
if(opt==4)printf("%lld\n",query(1,1,n,w[x],w[x]+siz[x]-1));
「完整代码」
#include<bits/stdc++.h>
#define ls u<<1
#define rs u<<1|1
#define ll long long
using namespace std;
const int N=1e5+5;
int n,m,r;
int cnt,dep[N],siz[N],hs[N],fa[N],w[N],top[N],pos[N];
ll p,rt[N],a[N],t[N<<2],tag[N<<2];
vector<int> g[N];
void dfs1(int u,int fath)
{fa[u]=fath;dep[u]=dep[fath]+1;siz[u]=1;hs[u]=-1;for(auto v:g[u]){if(v==fath) continue;dfs1(v,u);siz[u]+=siz[v];if(hs[u]==-1||siz[v]>siz[hs[u]]) hs[u]=v;}
}
void dfs2(int u,int t)
{top[u]=t;w[u]=++cnt;pos[cnt]=u;if(hs[u]!=-1) dfs2(hs[u],t);for(auto v:g[u])if(v!=fa[u]&&hs[u]!=v)dfs2(v,v);
}
void push_up(int u)
{t[u]=(t[ls]+t[rs])%p;
}
void build(int u,int l,int r)
{if(l==r){t[u]=a[pos[l]];return;}int mid=(l+r)>>1;build(ls,l,mid);build(rs,mid+1,r);push_up(u);
}
void push_down(int u,int l,int r)
{if(!tag[u]) return;tag[ls]=(tag[ls]+tag[u])%p;tag[rs]=(tag[rs]+tag[u])%p;int mid=(l+r)>>1;t[ls]=(t[ls]+tag[u]*(mid-l+1))%p;t[rs]=(t[rs]+tag[u]*(r-mid))%p;tag[u]=0;
}
void update(int u,int l,int r,int x,int y,ll k)
{if(y<l||r<x) return;if(x<=l&&r<=y){tag[u]=(tag[u]+k)%p;t[u]=(t[u]+k*(r-l+1))%p;return;}push_down(u,l,r);int mid=(l+r)>>1;if(x<=mid) update(ls,l,mid,x,y,k);if(y>mid) update(rs,mid+1,r,x,y,k);push_up(u);
}
ll query(int u,int l,int r,int x,int y)
{if(y<l||r<x) return 0;if(x<=l&&r<=y) return t[u]%p;push_down(u,l,r);int mid=(l+r)>>1;ll res=0;if(x<=mid) res=(res+query(ls,l,mid,x,y))%p;if(y>mid) res=(res+query(rs,mid+1,r,x,y))%p;return res;
}
void modify(int u,int v,ll k)
{while(top[u]^top[v]){if(dep[top[u]]<dep[top[v]]) swap(u,v);update(1,1,n,w[top[u]],w[u],k);u=fa[top[u]];}if(dep[u]<dep[v]) swap(u,v);update(1,1,n,w[v],w[u],k);
}
ll query(int u,int v)
{ll ans=0;while(top[u]^top[v]){if(dep[top[u]]<dep[top[v]]) swap(u,v);ans=(ans+query(1,1,n,w[top[u]],w[u]))%p;u=fa[top[u]];}if(dep[u]<dep[v]) swap(u,v);ans=(ans+query(1,1,n,w[v],w[u]))%p;return ans;
}
int LCA(int u,int v)
{while(top[u]^top[v]){if(dep[top[u]]<dep[top[v]]) swap(u,v);u=fa[top[u]];}if(dep[u]<dep[v]) swap(u,v);return v;
}
signed main()
{scanf("%d%d%d%lld",&n,&m,&r,&p);for(int i=1;i<=n;i++) scanf("%lld",&rt[i]);for(int i=1;i<n;i++){int u,v;scanf("%d%d",&u,&v);g[u].emplace_back(v);g[v].emplace_back(u);}dfs1(r,0);dfs2(r,r);build(1,1,n);while(m--){int opt,x,y;ll k;scanf("%d%d",&opt,&x);if(opt==1){scanf("%d%lld",&y,&k);modify(x,y,k); }if(opt==2){scanf("%d",&y);printf("%lld\n",query(x,y)); }if(opt==3){scanf("%lld",&k);update(1,1,n,w[x],w[x]+siz[x]-1,k);}if(opt==4)printf("%lld\n",query(1,1,n,w[x],w[x]+siz[x]-1));}return 0;
}
例2. P4315 月下“毛景树”
该题需要将边权下放,转换为点权,只需在 dfs1 加多一句即可。
至于为什么要把边权转向深度更深的节点,是因为对于每一条边 ( u , v ) (u,v) (u,v),节点 v v v 有且仅会出现一次,而一个节点可能会是多个儿子的父亲,将边权下放可以有效防止信息重复导致丢失。
void dfs1(int u,int fath)
{fa[u]=fath;dep[u]=dep[fath]+1;siz[u]=1;hs[u]=-1;for(auto [v,w]:g[u])//c++17 特性 auto []{if(v==fath) continue;dfs1(v,u);siz[u]+=siz[v];a[v]=w;//边权下放为点权if(hs[u]==-1||siz[v]>siz[hs[u]]) hs[u]=v;}
}
相应的,对于询问和操作,只需要访问再最后改成 w [ v ] + 1 w[v]+1 w[v]+1 和 w [ u ] w[u] w[u] 即可,比,避免了将 LCA计算进去。
例如:
void modify_cha(int u,int v,int k)
{while(top[u]^top[v]){if(dep[top[u]]<dep[top[v]]) swap(u,v);change(1,1,n,w[top[u]],w[u],k);u=fa[top[u]];}if(dep[u]<dep[v]) swap(u,v);change(1,1,n,w[v]+1,w[u],k);//这里需要 w[v]+1 有效防止更新了 lca
}
其他操作没有什么改变,注意需要将初始的边存一下,对于操作 Change k w 而言,需要判断一下哪个深度深或者谁是谁的父亲再去修改较深的点即可。
if(opt[1]=='h')
{int u=U[x],v=V[x];if(fa[v]==u) swap(u,v);//等价于if(dep[v]>dep[u]) swap(u,v);change(1,1,n,w[u],w[u],y);
}
「完整代码」
#include<bits/stdc++.h>
#define ls u<<1
#define rs u<<1|1
using namespace std;
const int N=1e5+5,INF=(1<<30);
int n,U[N],V[N],pos[N],a[N],t[N<<2],tag[N<<2],lazy[N<<2];
int cnt,fa[N],dep[N],siz[N],hs[N],w[N],top[N];
char opt[15];
struct Edge
{int v,w;
};
vector<Edge> g[N];
void dfs1(int u,int fath)
{fa[u]=fath;dep[u]=dep[fath]+1;siz[u]=1;hs[u]=-1;for(auto [v,w]:g[u]){if(v==fath) continue;dfs1(v,u);siz[u]+=siz[v];a[v]=w;if(hs[u]==-1||siz[v]>siz[hs[u]]) hs[u]=v;}
}
void dfs2(int u,int t)
{top[u]=t;w[u]=++cnt;pos[cnt]=u;if(hs[u]!=-1) dfs2(hs[u],t);for(auto [v,w]:g[u])if(v!=fa[u]&&hs[u]!=v)dfs2(v,v);
}
void push_up(int u)
{t[u]=max(t[ls],t[rs]);
}
void build(int u,int l,int r)
{lazy[u]=-1;if(l==r){t[u]=a[pos[l]];return;}int mid=(l+r)>>1;build(ls,l,mid);build(rs,mid+1,r);push_up(u);
}
void push_down(int u,int l,int r)
{if(lazy[u]!=-1){tag[ls]=tag[rs]=0;t[ls]=t[rs]=lazy[ls]=lazy[rs]=lazy[u];lazy[u]=-1;}if(tag[u]){tag[ls]+=tag[u];tag[rs]+=tag[u];t[ls]+=tag[u];t[rs]+=tag[u];tag[u]=0;}
}
void change(int u,int l,int r,int x,int y,int k)
{if(y<l||r<x) return;if(x<=l&&r<=y){tag[u]=0;t[u]=lazy[u]=k;return;}push_down(u,l,r);int mid=(l+r)>>1;if(x<=mid) change(ls,l,mid,x,y,k);if(y>mid) change(rs,mid+1,r,x,y,k);push_up(u);
}
void update(int u,int l,int r,int x,int y,int k)
{if(y<l||r<x) return;if(x<=l&&r<=y){tag[u]+=k;t[u]+=k;return;}push_down(u,l,r);int mid=(l+r)>>1;if(x<=mid) update(ls,l,mid,x,y,k);if(y>mid) update(rs,mid+1,r,x,y,k);push_up(u);
}
int qmax(int u,int l,int r,int x,int y)
{if(y<l||r<x) return -INF;if(x<=l&&r<=y) return t[u];push_down(u,l,r);int mid=(l+r)>>1,res=-INF;if(x<=mid) res=max(res,qmax(ls,l,mid,x,y));if(y>mid) res=max(res,qmax(rs,mid+1,r,x,y));return res;
}
void modify_cha(int u,int v,int k)
{while(top[u]^top[v]){if(dep[top[u]]<dep[top[v]]) swap(u,v);change(1,1,n,w[top[u]],w[u],k);u=fa[top[u]];}if(dep[u]<dep[v]) swap(u,v);change(1,1,n,w[v]+1,w[u],k);
}
void modify_upd(int u,int v,int k)
{while(top[u]^top[v]){if(dep[top[u]]<dep[top[v]]) swap(u,v);update(1,1,n,w[top[u]],w[u],k);u=fa[top[u]];}if(dep[u]<dep[v]) swap(u,v);update(1,1,n,w[v]+1,w[u],k);
}
int modify_qmax(int u,int v)
{int ans=-INF;while(top[u]^top[v]){if(dep[top[u]]<dep[top[v]]) swap(u,v);ans=max(ans,qmax(1,1,n,w[top[u]],w[u]));u=fa[top[u]];}if(dep[u]<dep[v]) swap(u,v);ans=max(ans,qmax(1,1,n,w[v]+1,w[u]));return ans;
}
signed main()
{scanf("%d",&n);for(int i=1;i<n;i++){int u,v,w;scanf("%d%d%d",&u,&v,&w);g[u].emplace_back((Edge){v,w});g[v].emplace_back((Edge){u,w});U[i]=u,V[i]=v;}dfs1(1,0);dfs2(1,1);build(1,1,n);while(scanf("%s",opt)&&opt[0]!='S'){int x,y,z;scanf("%d%d",&x,&y);if(opt[1]=='h'){int u=U[x],v=V[x];if(fa[v]==u) swap(u,v);change(1,1,n,w[u],w[u],y);}if(opt[1]=='o'){scanf("%d",&z);modify_cha(x,y,z);}if(opt[1]=='d'){scanf("%d",&z);modify_upd(x,y,z);}if(opt[1]=='a') printf("%d\n",modify_qmax(x,y));}return 0;
}
例3. P2146 [NOI2015] 软件包管理器
树链剖分后,用线段树维护区间1的信息,记上一次查询线段树根节点的值为 x 1 x1 x1,本次查询线段树根节点的值为 x 2 x2 x2,那么:
a n s = ∣ x 1 − x 2 ∣ ans=|x1-x2| ans=∣x1−x2∣
单条链网上不断修改,比较的好写。
「完整代码」
#include<bits/stdc++.h>
#define ls u<<1
#define rs u<<1|1
using namespace std;
const int N=1e5+5;
int n,Q,t[N<<2],tag[N<<2];
int cnt,fa[N],dep[N],hs[N],siz[N],w[N],top[N];
vector <int> g[N];
char opt[15];
void dfs1(int u,int fath)
{fa[u]=fath;dep[u]=dep[fath]+1;siz[u]=1;hs[u]=-1;for(auto v:g[u]){if(v==fath) continue;dfs1(v,u);siz[u]+=siz[v];if(hs[u]==-1||siz[v]>siz[hs[u]]) hs[u]=v;}
}
void dfs2(int u,int t)
{top[u]=t;w[u]=++cnt;if(hs[u]!=-1) dfs2(hs[u],t);for(auto v:g[u])if(v!=hs[u]&&fa[u]!=v)dfs2(v,v);
}
void push_up(int u)
{t[u]=t[ls]+t[rs];
}
void build(int u,int l,int r)
{tag[u]=-1;if(l==r){return;}int mid=(l+r)>>1;build(ls,l,mid);build(rs,mid+1,r);push_up(u);
}
void push_down(int u,int l,int r)
{if(tag[u]==-1) return;tag[ls]=tag[rs]=tag[u];int mid=(l+r)>>1;t[ls]=(mid-l+1)*tag[u];t[rs]=(r-mid)*tag[u];tag[u]=-1;
}
void update(int u,int l,int r,int x,int y,int k)
{if(y<l||r<x) return;if(x<=l&&r<=y){tag[u]=k;t[u]=(r-l+1)*k;return;}push_down(u,l,r);int mid=(l+r)>>1;if(x<=mid) update(ls,l,mid,x,y,k);if(y>mid) update(rs,mid+1,r,x,y,k);push_up(u);
}
void modify(int u,int v,int k)
{while(top[u]^top[v]){if(dep[top[u]]<dep[top[v]]) swap(u,v);update(1,1,n,w[top[u]],w[u],k);u=fa[top[u]];}if(dep[u]<dep[v]) swap(u,v);update(1,1,n,w[v],w[u],k);
}
signed main()
{scanf("%d",&n);for(int i=2;i<=n;i++){int u;scanf("%d",&u);++u;g[u].push_back(i);g[i].push_back(u);}dfs1(1,0);dfs2(1,1);build(1,1,n);scanf("%d",&Q);while(Q--){int x,pre;scanf("%s%d",opt,&x);++x;pre=t[1];if(opt[0]=='i'){modify(1,x,1);printf("%d\n",abs(t[1]-pre));}if(opt[0]=='u'){update(1,1,n,w[x],w[x]+siz[x]-1,0);printf("%d\n",abs(t[1]-pre));}}return 0;
}
例4. P2486 [SDOI2011] 染色
有一些思维含量的题。
统计颜色段数量时不能简单地区间加法,线段树还应维护区间最左颜色和区间最右颜色。
合并时,如果 S ( l , k ) S(l,k) S(l,k) 的右端与 S ( k + 1 , r ) S(k+1,r) S(k+1,r) 的左端颜色相同,那么 S ( l , r ) = S ( l , k ) + S ( k + 1 , r ) − 1 S(l,r)=S(l,k)+S(k+1,r)-1 S(l,r)=S(l,k)+S(k+1,r)−1(减去重复的那一个);
否则 S ( l , r ) = S ( l , k ) + S ( k + 1 , r ) S(l,r)=S(l,k)+S(k+1,r) S(l,r)=S(l,k)+S(k+1,r) 正常合并。
核心代码:
void push_up(int u,int mid)
{t[u]=t[ls]+t[rs]-(c[mid]==c[mid+1]);
}
void build(int u,int l,int r)
{if(l==r){t[u]=1;return;}int mid=(l+r)>>1;build(ls,l,mid);build(rs,mid+1,r);push_up(u,mid);
}
void push_down(int u,int mid)
{if(!tag[u]) return;tag[ls]=tag[rs]=c[mid]=c[mid+1]=tag[u];t[ls]=t[rs]=1;tag[u]=0;
}
void update(int u,int l,int r,int x,int y,int k)
{if(y<l||r<x) return;if(x<=l&&r<=y){tag[u]=c[l]=c[r]=k;t[u]=1;return;}int mid=(l+r)>>1;push_down(u,mid);if(x<=mid) update(ls,l,mid,x,y,k);if(y>mid) update(rs,mid+1,r,x,y,k);push_up(u,mid);
}
int query(int u,int l,int r,int x,int y)
{if(y<l||r<x) return 0;if(x<=l&&r<=y) return t[u];int mid=(l+r)>>1,res=0;push_down(u,mid);if(x<=mid) res+=query(ls,l,mid,x,y);if(y>mid) res+=query(rs,mid+1,r,x,y);if(x<=mid&&y>mid&&c[mid]==c[mid+1]) --res;return res;
}
void modify(int u,int v,int k)
{while(top[u]^top[v]){if(dep[top[u]]<dep[top[v]]) swap(u,v);update(1,1,n,w[top[u]],w[u],k);u=fa[top[u]];}if(dep[u]<dep[v]) swap(u,v);update(1,1,n,w[v],w[u],k);
}
int query(int u,int v)
{int ans=0,x=u,y=v;while(top[u]^top[v]){if(dep[top[u]]<dep[top[v]]) swap(u,v);ans+=query(1,1,n,w[top[u]],w[u]);u=fa[top[u]];}if(dep[u]<dep[v]) swap(u,v);ans+=query(1,1,n,w[v],w[u]);u=x,v=y;while(top[u]^top[v]){if(dep[top[u]]<dep[top[v]]) swap(u,v);if(c[w[top[u]]]==c[w[fa[top[u]]]]) --ans;u=fa[top[u]];}return ans;
}
(完整代码就不贴了咕咕咕)
例5. P3979 遥远的国度
本题操作 3 3 3 看似需要换根,但是对于树剖来说换根就需要重新 dfs,不如在原先预处理出的数据上进行询问。
(此处引用了 Farkas_W 的 blog 关于树链剖分"换根操作"笔记的部分内容)
考虑分类讨论:
- 情况 1 1 1:当 x = r o o t x=root x=root 时, x x x 就是此时整棵树的根,那么就是全局修改(查询)。
- 情况 2 2 2:当 r o o t root root 在 x x x 子树中时,就需要特别判断了,我们可以发现此时 x x x 的真正子树是包括除了 r o o t root root 方向上的子树之外其他所有节点。
- 情况 3 3 3 :其他情况下 x x x 的子树以 r o o t root root 为根和以 1 1 1 为根是一样的。
int query(int u)
{if(u==root) return query(1,1,n,1,n);if(w[root]>=w[u]&&w[root]<=w[u]+siz[u]-1){int v=find(u,root);return negation_query(1,1,n,w[v],w[v]+siz[v]-1);}return query(1,1,n,w[u],w[u]+siz[u]-1);
}
「完整代码」
#include<bits/stdc++.h>
#define ls u<<1
#define rs u<<1|1
using namespace std;
const int N=1e5+5,INF=2147483647;
int n,m,root,a[N],b[N],t[N<<2],tag[N<<2];
int cnt,fa[N],dep[N],siz[N],hs[N],w[N],top[N];
vector <int> g[N];
void dfs1(int u,int fath)
{fa[u]=fath;dep[u]=dep[fath]+1;siz[u]=1;hs[u]=-1;for(auto v:g[u]){if(v==fath) continue;dfs1(v,u);siz[u]+=siz[v];if(hs[u]==-1||siz[v]>siz[hs[u]]) hs[u]=v;}
}
void dfs2(int u,int t)
{top[u]=t;w[u]=++cnt;b[cnt]=a[u];if(hs[u]!=-1) dfs2(hs[u],t);for(auto v:g[u])if(v!=hs[u]&&fa[u]!=v)dfs2(v,v);
}
void push_up(int u)
{t[u]=min(t[ls],t[rs]);
}
void build(int u,int l,int r)
{if(l==r){t[u]=b[l];return;}int mid=(l+r)>>1;build(ls,l,mid);build(rs,mid+1,r);push_up(u);
}
void push_down(int u,int l,int r)
{if(!tag[u]) return;tag[ls]=tag[rs]=tag[u];t[ls]=t[rs]=tag[u];tag[u]=0;
}
void update(int u,int l,int r,int x,int y,int k)
{if(y<l||r<x) return;if(x<=l&&r<=y){tag[u]=t[u]=k;return;}push_down(u,l,r);int mid=(l+r)>>1;if(x<=mid) update(ls,l,mid,x,y,k);if(y>mid) update(rs,mid+1,r,x,y,k);push_up(u);
}
int query(int u,int l,int r,int x,int y)
{if(y<l||r<x) return INF;if(x<=l&&r<=y) return t[u];push_down(u,l,r);int mid=(l+r)>>1,res=INF;if(x<=mid) res=min(res,query(ls,l,mid,x,y));if(y>mid) res=min(res,query(rs,mid+1,r,x,y));return res;
}
int negation_query(int u,int l,int r,int x,int y)
{if(y<l||r<x) return t[u];if(x<=l&&r<=y) return INF;push_down(u,l,r);int mid=(l+r)>>1,res=INF;res=min(res,negation_query(ls,l,mid,x,y));res=min(res,negation_query(rs,mid+1,r,x,y));return res;
}
void modify(int u,int v,int k)
{while(top[u]^top[v]){if(dep[top[u]]<dep[top[v]]) swap(u,v);update(1,1,n,w[top[u]],w[u],k);u=fa[top[u]];}if(dep[u]<dep[v]) swap(u,v);update(1,1,n,w[v],w[u],k);
}
int find(int u,int v)
{while(top[u]^top[v]){if(dep[top[u]]<dep[top[v]]) swap(u,v);if(fa[top[u]]==v) return top[u];u=fa[top[u]];}if(dep[u]<dep[v]) swap(u,v);return hs[v];
}
int query(int u)
{if(u==root) return query(1,1,n,1,n);if(w[root]>=w[u]&&w[root]<=w[u]+siz[u]-1){int v=find(u,root);return negation_query(1,1,n,w[v],w[v]+siz[v]-1);}return query(1,1,n,w[u],w[u]+siz[u]-1);
}
signed main()
{scanf("%d%d",&n,&m);for(int i=1;i<n;i++){int u,v;scanf("%d%d",&u,&v);g[u].push_back(v);g[v].push_back(u);}for(int i=1;i<=n;i++)scanf("%d",a+i);scanf("%d",&root);dfs1(root,0);dfs2(root,root);build(1,1,n);while(m--){int opt,x,y,k;scanf("%d",&opt);if(opt==1) scanf("%d",&root);if(opt==2) scanf("%d%d%d",&x,&y,&k),modify(x,y,k);if(opt==3) scanf("%d",&x),printf("%d\n",query(x));}return 0;
}
三、长链剖分
(Tip:由于长链剖分比较少用,所以这部分的篇幅会稍微短一些,绝对不是因为笔者没学长链剖分,快速带过)
3.1 概念
与重链剖分类似,我们设一个节点中深度最深的子节点为长节点,设该节点到长节点的边为重边,其他边为轻边。
然后我们把首尾相连的重边组成长链,落单的一个节点也被视作一条长链。
我们就把树分成了若干条互不相交的长链。
3.2 性质
- 性质 1 1 1:节点 u u u 与节点 f a t o p u fa_{top_u} fatopu 一定不在同一条长链上。
证明:略。与重链剖分性质 2 2 2 的证明一样。
- 性质 2 2 2:从根节点到树上任意一点的路径上的轻边数不超过 n \sqrt n n。
证明:如果一个点 u u u,从一条长链跳到另一条长链上,那么跳跃到这条长链的长度不会小于之前的长链的长度。那么在最坏的情况下,长链长度分别为: 1 , 2 , 3 , . . . , n 1,2,3,...,\sqrt n 1,2,3,...,n,也就是最多跳跃 n \sqrt n n 次,比重链剖分的 log n \log n logn 稍劣一些。
3.3 时间复杂度 & 应用
- 从根到任意一条链最劣需要经过 O ( n ) O(\sqrt n) O(n) 条链,复杂度不会证(逃)。
长链剖分求树上 k k k 级祖先:
n log n n \log n nlogn 倍增预处理求出每个节点 u u u 的 2 k 2^k 2k 级祖先,以及对于每条长链,从长链顶端向上 / 向下
i i i 步分别能走到哪个节点,其中 i i i 不大于长链深度。此外,预处理每个数在二进制下的最高位,记为 h i h_i hi。
查询 ( u , k ) (u,k) (u,k) ( u u u 的 k k k 级祖先)
首先跳到 u u u 的 2 h k 2^{h_k} 2hk 级祖先 v v v,由于我们预处理了从 v v v 所在长链顶端 t o p top top 向上 / 下走不超过链长步分别到哪个节点,故不难直接查询。综上,时间复杂度为 O ( n log n ) O(n \log n) O(nlogn)。
四、习题
以下为「重链剖分」习题(没有将例题讲解算在这里):
- P4315 月下“毛景树”
- P4092 [HEOI2016/TJOI2016] 树
- P4216 [SCOI2015] 情报传递
- P4069 [SDOI2016] 游戏 【前置:李超线段树】
- CF916E Jamie and Tree
以下为「长链剖分」习题:
- P5903 【模板】树上 K 级祖先
- CF1009F Dominant Indices
五、结语
咕咕咕,终于写完了,咕了都快一个月了(),Markdown 都快卡死了。
以后学了长链剖分再来补吧咕咕咕。
( 1 k 1k 1k 行不卡才怪)









![[OS] mmap() 函数的参数及其作用](https://i-blog.csdnimg.cn/direct/0d2b9eeb46084a5689fa3934f9d93aee.png)