随机游走之 个人的简单理解

随机游动（Random Walk）是指一个质点（或粒子）在某个空间中按照一定的概率规则随机地移动。最基本的模型是一维简单随机游动（1D Simple Random Walk）。

图1-1

对于一维随机游走问题，初始位置x=n,单位时间每次向左或向右移动一个单位长度，p=12  设边界为0和w，0≤n≤w，质点到达边界后便停止运动。

若用Sn表示初始位置为x=n时最终落入边界x=0的概率，Tn表示初始位置为x=n最终落入边界x=w的概率。显然我们会有so=1，sw=0，即初始位置为边界的情况. 

证明：

由全概率公式得到              sn=12sn-1+12sn+1

变形得                       sn+1=2sn-sn-1

移项得                    Sn+1-Sn=Sn-Sn-1

递推得                sn-sn-1=…=s1-s0=k

累加                             sn=kn+s0

将s0=1,sw=0代入后s0=1，c=1，kw+1=0 所以说

Sn=1-1wn=w-nw

因此可以得出结论w→∞，没有右侧的边界， sn=1，也就是说（落入0的概率趋近于1）。如果同时消除左右边界的话，无穷次经过原点。

如果对简单的一维模型升级成二维，Polya已经证明了必然会回到原点，个人的理解是一维到二维的延伸，只不过概率改变成 p=14，如果延伸到三维p=16，我想只要时间足够长，应该就能够回来。然而数学还是要写出来，关键大概是调和级数不收敛吧

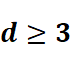求证下：随机游动在Rd上对称，d=1,2时是常返的，d≥3是暂留的。

返回到原点的话可以理解成左右走的数目相等，所以必然是偶数次

U2n=2nn122n

引入一下Stirling 公式：n!≈2πnnⅇn

二项式的系数                  2nn≈4nπn

即u2n=4nπn14n≈1πn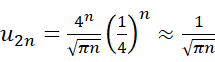

计算所有回到0时候的概率只需要将所有的情况汇总f=n=1∞u2n

下面推广到n维，n很大的时候，随机游走的位置趋近于正态分布，使用局部极限定理做一个近似，

Und=Cdnd2

就是原点处的概率密度。

 Cd为常数不影响敛散性，同理还是将所有可能的概率累加，

n=1∞und=n=1∞1nd2

对于这个幂级数d≥3收敛。

换一个角度来理解，上升到三维的时候，回到原点的可能性随着每一步都在减小，而回不到原始点的可能性不断增大，类似于走回原点需要一个门限的步数，加入发散就一定会使得概率超过门槛下限（至少一次），可是如果是收敛的有可能达不到门槛。