DataWhale—PumpkinBook（TASK03对数几率回归）

一、课程组成及结构

课程开源地址及相关视频链接：（当然这里也希望大家支持一下正版西瓜书和南瓜书图书，支持文睿、秦州等等致力于开源生态建设的大佬✿✿ヽ(°▽°)ノ✿）

Datawhale-学用 AI,从此开始

【吃瓜教程】《机器学习公式详解》（南瓜书）与西瓜书公式推导_哔哩哔哩_bilibili

具体学习安排如下：

二、课程的正文部分

对数几率回归

首先先学习一下概念（来源百度）：
对数几率回归，简称对率回归，又称逻辑回归，是使用Sigmoid函数作为联系函数时的广义线性模型，是广义线性模型的一个特例。也是利用广义线性模型解决二分类任务的一种方法。

logistic回归是一种广义线性回归（generalized linear model），也是是拟合分类数据（尤其是二元响应数据）的模型的最常用方法之一，与多重线性回归分析有很多相同之处。它们的模型形式基本上相同，都具有 w‘x+b，其中w和b是待求参数，其区别在于他们的因变量不同，多重线性回归直接将w‘x+b作为因变量，即y =w‘x+b，而logistic回归则通过函数L将w‘x+b对应一个隐状态p，p =L(w‘x+b),然后根据p 与1-p的大小决定因变量的值。如果L是logistic函数，就是logistic回归，如果L是多项式函数就是多项式回归。logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释，多类可以使用softmax方法进行处理。实际中最为常用的就是二分类的logistic回归。与线性回归不同，逻辑回归可以直接预测概率（限制为（0,1）区间的值）;此外，与其他一些分类器（如 Naive Bayes）预测的概率相比，这些概率经过了很好的校准。Logistic 回归保留训练数据的边际概率。模型的系数还提供了每个输入变量的相对重要性的一些提示。

熟悉推导过程的朋友可以直接跳过》》》》》》QAQ

Logistic 回归模型假定观测 y值的对数几率可以表示为 K 输入变量 x的线性函数

使用逻辑回归进行分类，就是要找到绿色这样的分界线，使其能够尽可能地对样本进行正确分类，也就是能够尽可能地将两种样本分隔开来。因此我们可以构造这样一个函数，来对样本集进行分隔：

其中 i=1,2,...m，表示第 i个样本, n 表示特征数,当 z(x(i))>0z(x(i))>0 时，对应着样本点位于分界线上方，可将其分为"1"类；当 z(x(i))<0z(x(i))<0 时，样本点位于分界线下方，将其分为“0”类。

逻辑回归作为分类算法，它的输出是0/1。那么如何将输出值转换成0/1呢？

这就需要一个新的函数——sigmoid 函数

sigmoid 函数定义如下，为了实现根据所有输入预测出类别，为此引入了sigmoid函数,sigmoid函数刚好也有二分类的功能。

与南瓜书公式推导可以相互对照参考

其函数图像为：

由函数图像可以看出， sigmoid函数可以很好地将 (−∞,∞) 内的数映射到 (0,1) 上。

为什么要使用sigmoid函数作为假设？

因为线性回归模型的预测值为一般为大于1的实数，而样本的类标签为（0,1），我们需要将分类任务的真实标记y与线性回归模型的预测值联系起来，也就是找到广义线性模型中的联系函数。如果选择单位阶跃函数的话，它是不连续的不可微。而如果选择sigmoid函数，它是连续的，而且能够将z转化为一个接近0或1的值。

当z=0时，p=0.5
当z>0时，p>0.5  归为1类
当z<0时，p<0.5  归为0类

因此我们可以认为g（z）>= 0.5时为“1”类，反之为“0”类

二项逻辑斯蒂回归模型是一种分类模型，由条件概率分布 p(Y|X)表示，形式为参数化的逻辑斯谛分布。这里，随机变量 X 取值为实数，随机变量 Y 取值为 1或0。可通过监督学习的方法来估计模型参数。二项逻辑斯谛回归模型是如下的条件概率分布为

这里补充给出《统计学习方法》一点书本上的内容，以供大家参考学习。

其中， x∈Rn 是输入， Y∈{0,1} 是输出， θ 是参数。

对于 Y=1 有

而上式分子不等于0，则有

最终逻辑回归模型函数为，此为分类结果为1的概率

一下分别为则Sigmoid函数和逻辑回归模型函数

#导入库
import math
import csv
import numpy as np#读取数据集之后操作def sigmoid(x):return 1.0/(1 + np.exp(-x))

代价函数

使用 sigmoid 函数求解出来的值为类1的后验估计 p(y=1|x,θ),故我们可以得到：

其中 p(y=1|x,θ)表示样本分类为 y=1 的概率，而 p(y=0|x,θ) 表示样本分类为 y=0的概率。

得到其似然函数为：

对数似然函数为：

所得的代价函数，对求 logL(θ)的最大值来求得参数θ的值。将代价函数做了以下改变：

此时只需对 J(θ)求最小值，便得可以得到参数 θ。


import math
import csv
import numpy as npdef J(theta, X, Y, theLambda=0):m, n = X.shapeh = sigmoid(np.dot(X, theta))J = (-1.0/m)*(np.dot(np.log(h).T, Y)+np.dot(np.log(1-h).T, 1-Y)) + (theLambda/(2.0*m))*np.sum(np.square(theta[1:]))return J.flatten()[0]

梯度下降

梯度下降法过程为

求解梯度:


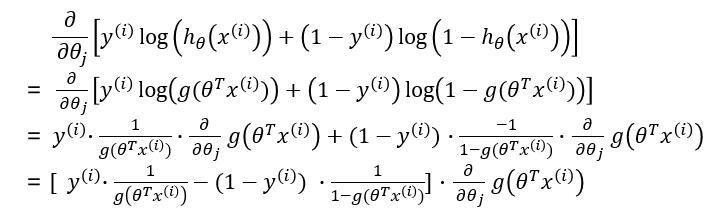
import math
import csv
import numpy as npdef gradient_sgd(X, Y, alpha=0.01, epsilon=0.00001, maxloop=1000, theLambda=0.0):m, n = X.shapetheta = np.zeros((n, 1))cost = J(theta, X, Y)costs = [cost]thetas = [theta]# 随机梯度下降count = 0flag = Falsewhile count < maxloop:if flag:breakfor i in range(m):h = sigmoid(np.dot(X[i].reshape((1, n)), theta))theta = theta - alpha * ((1.0 / m) * X[i].reshape((n, 1)) * (h - Y[i]) + (theLambda / m) * np.r_[[[0]], theta[1:]])thetas.append(theta)cost = J(theta, X, Y, theLambda)costs.append(cost)if abs(costs[-1] - costs[-2]) < epsilon:flag = Truebreakcount += 1if count % 100 == 0:print("cost:", cost)return thetas, costs, count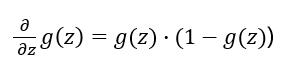

因此有：

综上：

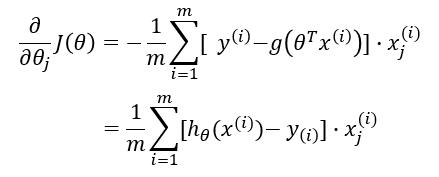
牛顿法

牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f (x) = 0的根。牛顿法最大的特点就在于它的收敛速度很快。

首先，选择一个接近函数 f (x)零点的 x0，计算相应的 f (x0) 和切线斜率f ' (x0)（这里f ' 表示函数 f 的导数）。然后我们计算穿过点(x0, f (x0)) 并且斜率为f '(x0)的直线和 x 轴的交点的x坐标，也就是求如下方程的解：

我们将新求得的点的 x 坐标命名为x1，通常x1会比x0更接近方程f (x) = 0的解。因此我们现在可以利用x1开始下一轮迭代。迭代公式可化简为如下所示：

已经证明，如果f ' 是连续的，并且待求的零点x是孤立的，那么在零点x周围存在一个区域，只要初始值x0位于这个邻近区域内，那么牛顿法必定收敛。并且，如果f ' (x)不为0, 那么牛顿法将具有平方收敛的性能. 粗略的说，这意味着每迭代一次，牛顿法结果的有效数字将增加一倍。下图为一个牛顿法执行过程的例子。

而在逻辑回归中牛顿法更新方式为：

本质上去看，牛顿法是二阶收敛，梯度下降是一阶收敛，所以牛顿法就更快。如果更通俗地说的话，比如你想找一条最短的路径走到一个盆地的最底部，梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步，牛顿法在选择方向时，不仅会考虑坡度是否够大，还会考虑你走了一步之后，坡度是否会变得更大。所以，可以说牛顿法比梯度下降法看得更远一点，能更快地走到最底部。（牛顿法目光更加长远，所以少走弯路；相对而言，梯度下降法只考虑了局部的最优，没有全局思想。）

#导入库
import math
import csv
import numpy as npdef gradient_newton(X, Y, epsilon=0.00001, maxloop=1000, theLambda=0.0):m, n = X.shapetheta = np.zeros((n, 1))cost = J(theta, X, Y)costs = [cost]thetas = [theta]count = 0while count < maxloop:delta_J = 0.0H = 0.0for i in range(m):h = sigmoid(np.dot(X[i].reshape((1, n)), theta))delta_J += X[i] * (h - Y[i])H += h.T * (1 - h) * X[i] * X[i].Tdelta_J /= mH /= mprint(H, delta_J)theta = theta - 1.0 / H * delta_Jthetas.append(theta)cost = J(theta, X, Y, theLambda)costs.append(cost)if abs(costs[-1] - costs[-2]) < epsilon:breakcount += 1if count % 100 == 0:print("cost:", cost)return thetas, costs, count