题目链接
Problem Statement
Takahashi and Aoki will play a game using cards with numbers written on them.
Initially, Takahashi has N N N cards with numbers A 1 , … , A N A_1, \ldots, A_N A1,…,AN in his hand, Aoki has M M M cards with numbers B 1 , … , B M B_1, \ldots, B_M B1,…,BM in his hand, and there are L L L cards with numbers C 1 , … , C L C_1, \ldots, C_L C1,…,CL on the table.
Throughout the game, both Takahashi and Aoki know all the numbers on all the cards, including the opponent’s hand.
Starting with Takahashi, they take turns performing the following action:
- Choose one card from his hand and put it on the table. Then, if there is a card on the table with a number less than the number on the card he just played, he may take one such card from the table into his hand.
The player who cannot make a move first loses, and the other player wins. Determine who wins if both players play optimally.
It can be proved that the game always ends in a finite number of moves.
中文题意
问题陈述
高桥和青木将用写有数字的卡片玩一个游戏。
最初,高桥手中有 N N N 张写有数字 A 1 , … , A N A_1, \ldots, A_N A1,…,AN 的纸牌,青木手中有 M M M 张写有数字 B 1 , … , B M B_1, \ldots, B_M B1,…,BM 的纸牌,桌上有 L L L 张写有数字 C 1 , … , C L C_1, \ldots, C_L C1,…,CL 的纸牌。
在整个游戏过程中,高桥和青木都知道所有牌上的所有数字,包括对手手中的牌。
从高桥开始,他们轮流进行以下操作:
- 从自己手中选择一张牌放在桌上。然后,如果桌上有一张牌的数字小于他刚刚打出的牌上的数字,他可以从桌上拿一张这样的牌放入自己的手牌中。
不能先出牌的一方输,另一方赢。如果双方都以最佳方式出牌,谁会赢?
可以证明游戏总是在有限步数内结束。
Constraints
- 1 ≤ N , M , L 1 \leq N, M, L 1≤N,M,L
- N + M + L ≤ 12 N + M + L \leq 12 N+M+L≤12
- 1 ≤ A i , B i , C i ≤ 1 0 9 1 \leq A_i, B_i, C_i \leq 10^9 1≤Ai,Bi,Ci≤109
- All input values are integers.
Input
The input is given from Standard Input in the following format:
N N N M M M L L L
A 1 A_1 A1 … \ldots … A N A_N AN
B 1 B_1 B1 … \ldots … B M B_M BM
C 1 C_1 C1 … \ldots … C L C_L CL
Output
Print Takahashi if Takahashi wins, and Aoki if Aoki wins.
Sample Input 1
1 1 2
2
4
1 3
Sample Output 1
Aoki
The game may proceed as follows (not necessarily optimal moves):
- Takahashi plays 2 2 2 from his hand to the table, and takes 1 1 1 from the table into his hand. Now, Takahashi’s hand is ( 1 ) (1) (1), Aoki’s hand is ( 4 ) (4) (4), and the table cards are ( 2 , 3 ) (2,3) (2,3).
- Aoki plays 4 4 4 from his hand to the table, and takes 2 2 2 into his hand. Now, Takahashi’s hand is ( 1 ) (1) (1), Aoki’s hand is ( 2 ) (2) (2), and the table cards are ( 3 , 4 ) (3,4) (3,4).
- Takahashi plays 1 1 1 from his hand to the table. Now, Takahashi’s hand is ( ) () (), Aoki’s hand is ( 2 ) (2) (2), and the table cards are ( 1 , 3 , 4 ) (1,3,4) (1,3,4).
- Aoki plays 2 2 2 from his hand to the table. Now, Takahashi’s hand is ( ) () (), Aoki’s hand is ( ) () (), and the table cards are ( 1 , 2 , 3 , 4 ) (1,2,3,4) (1,2,3,4).
- Takahashi cannot make a move and loses; Aoki wins.
Sample Input 2
4 4 4
98 98765 987654 987654321
987 9876 9876543 98765432
123 12345 1234567 123456789
Sample Output 2
Takahashi
Sample Input 3
1 1 8
10
10
1 2 3 4 5 6 7 8
Sample Output 3
Aoki
解法
游戏的状态可以由当前玩家和每张牌的所有者(高桥的、青木的或桌上的)来表示,总共有 2 × 3 N + M + L 2\times 3^{N+M+L} 2×3N+M+L 种状态。
每走一步,两个人手中的牌上的数字之和就会减少,意味着我们永远不会两次回到相同的状态。因此,我们可以通过记忆递归法找到答案,即检查哪位棋手总是在每个状态下获胜。
更具体地说,如果一个点是必败的点,那么无论下一步怎么走,只能走到对方的必胜点;如果一个点是必胜点,无论怎么走,只能走到对方的必败点。这可以自然地表达为一个递归函数,并且可以记忆。
在 S = N + M + L S=N+M+L S=N+M+L 中,有 O ( 3 S ) O(3^S) O(3S) 个状态和 O ( S 2 ) O(S^2) O(S2) 个转换,因此总共用了 O ( 3 S S 2 ) O(3^S S^2) O(3SS2) 个时间来解决这个问题。
#include <bits/stdc++.h>
using namespace std;
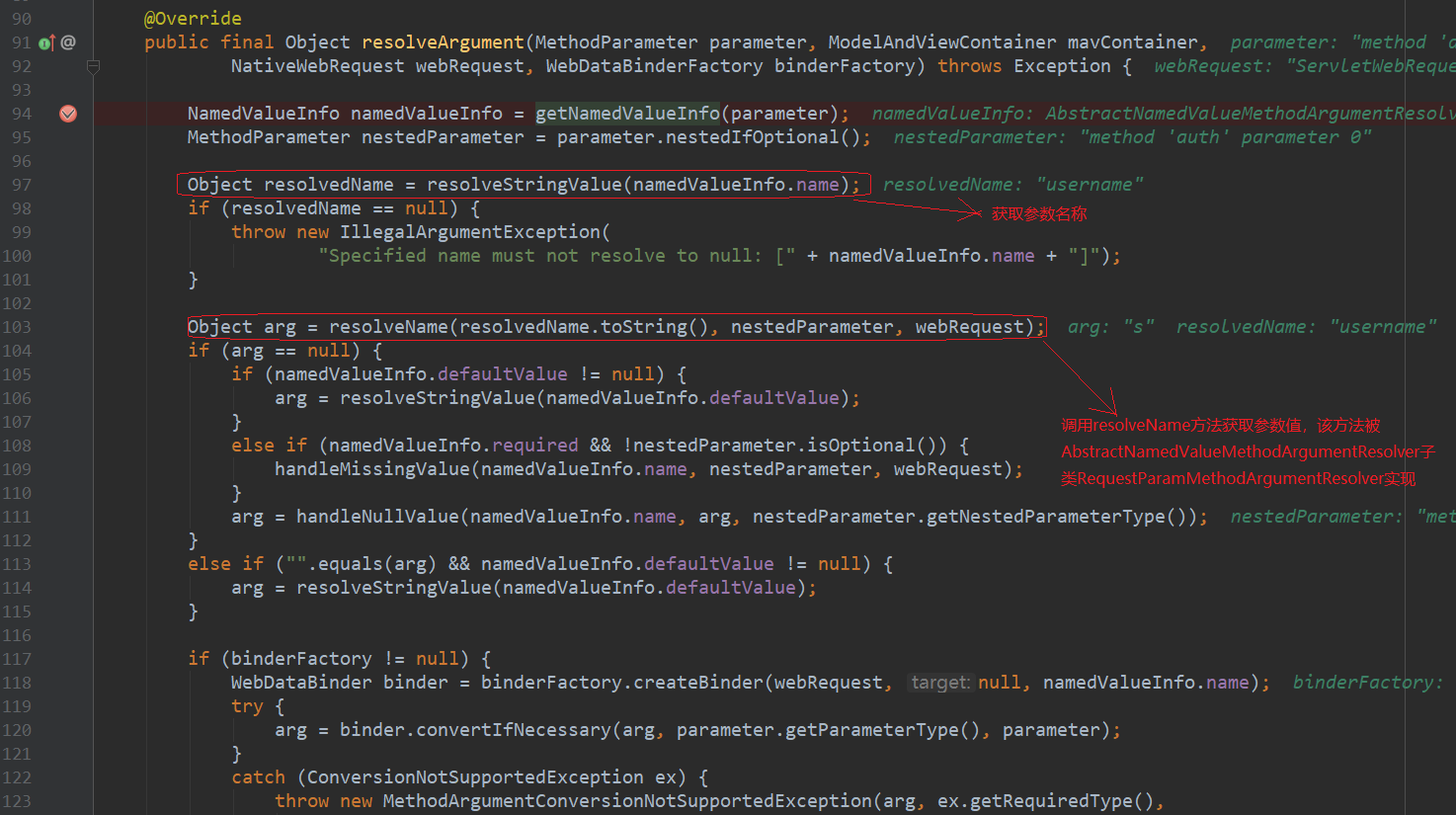
int main(){int N, M, L;cin >> N >> M >> L;vector<int> A(N + M + L);for (int i = 0; i < N + M + L; i++){cin >> A[i];}int S = N + M + L;vector<int> T(S + 1);T[0] = 1;for (int i = 0; i < S; i++){T[i + 1] = T[i] * 3;}auto get = [&](int x, int i){return x / T[i] % 3;};vector<vector<bool>> used(2, vector<bool>(T[S], false));vector<vector<bool>> dp(2, vector<bool>(T[S], false));auto dfs = [&](auto dfs, int t, int s) -> bool {if (!used[t][s]){for (int i = 0; i < S; i++){if (get(s, i) == t){int s2 = s - T[i] * t + T[i] * 2;if (!dfs(dfs, t ^ 1, s2)){dp[t][s] = true;}for (int j = 0; j < S; j++){if (A[j] < A[i] && get(s, j) == 2){int s3 = s2 - T[j] * 2 + T[j] * t;if (!dfs(dfs, t ^ 1, s3)){dp[t][s] = true;}}}}}used[t][s] = true;}return dp[t][s];};int C = 0;for (int i = N; i < N + M; i++){C += T[i];}for (int i = N + M; i < S; i++){C += T[i] * 2;}if (dfs(dfs, 0, C)){cout << "Takahashi" << endl;} else {cout << "Aoki" << endl;}
}