1. 第 N 个泰波那契数（easy）

1. 题目链接：1137. 第 N 个泰波那契数

2. 题目描述

3.题目分析

这题我们要求第n个泰波那契Tn的值，很明显的使用动态规划算法。

4.动态规划算法流程

1. 状态表示：

根据题目的要求及公式直接定义出状态表示：我们以第i个位置为结尾，dp表第i个位置的值表示第i个泰波那契的值。
 

2. 状态转移方程：

根据公式我们确定dp[i]的值或者状态通过状态表示方程表示是dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3]

3. dp表初始化：

 从我们的递推公式可以看出， dp[i] 在i = 0 以及 i = 1 的时候是没有办法进行推导的，因
为 dp[-2] 或 dp[-1] 不是一个有效的数据。因此我们需要在填表之前，将 0, 1, 2 位置的值初始化。题目中已经告诉我们 dp[0] = 0, dp[1] = dp[2] = 1 ，我们按照题目的值初始化

4. 填表顺序：

要求dp[i]的值就要先确定dp[i - 1]、 dp[i - 2]、dp[i - 3]的值，因此dp表的填表顺序就是从左往右

5. 返回值：

题目要求第n个数的值，我们就应该返回 dp[n] 的值。

5.算法代码

class Solution {
public:int tribonacci(int n) {vector<int> dp(n + 1);if(n == 0) return 0;//对于n为0,1,2的特殊情况，我们需要处理一下防止越界if(n == 1 || n == 2) return 1;dp[0] = 0,dp[1] = 1,dp[2] = 1;for(int i = 3;i <= n;i++){dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3];}return dp[n];}
};

6.滚动数组优化：

我们发现在求解上述问题的过程中，我们只需要知道该位置前三的位置的值相加就行，因此开辟O(n)的空间消耗完全没有必要，我们使用滚动数组来进行优化（滚动数组只是一种形象的说法，并不一定是数组）

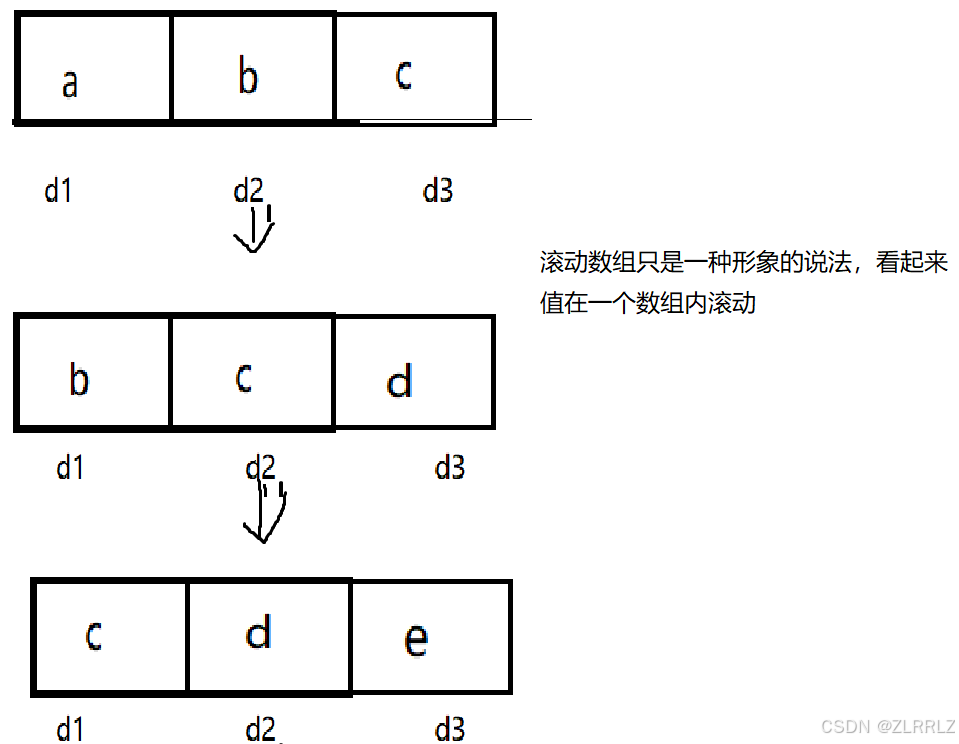
算法代码展示

class Solution {
public:int tribonacci(int n) {int a = 0,b = 1,c = 1,d = 0;if(n == 0) return 0;if(n == 1 || n == 2) return 1;for(int i = 3;i <= n;i++){d = a + b + c;a = b;b = c;c = d;}return d;}
};