摘要
本文基于MATLAB/Simulink环境,对四旋翼无人机进行了PID双闭环控制设计与仿真研究。通过分析四旋翼无人机的动力学模型与运动学模型,建立了姿态和位置双闭环控制系统,以实现无人机的稳定飞行与精确轨迹跟踪。仿真实验验证了该控制策略的有效性,表明系统具有良好的动态性能和稳态精度。
理论
1. 四旋翼无人机模型
四旋翼无人机模型由以下两部分组成:
-
动力学模型: 描述了无人机的力和力矩方程:

-
运动学模型: 描述无人机的位姿变化:
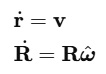
2. PID双闭环控制
为了实现姿态和位置的精确控制,采用双闭环PID控制:
-
内环控制(姿态控制):用于控制无人机的俯仰、横滚和偏航角。
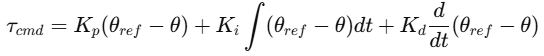
-
外环控制(位置控制):用于控制无人机的三维空间位置。
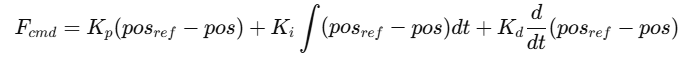
实验结果
-
姿态控制 仿真结果显示,在给定姿态变化指令后,系统能够快速响应,姿态误差迅速收敛,且无明显超调。
-
位置控制 在位置轨迹跟踪仿真中,无人机能够精确跟随参考轨迹,系统位置误差在稳态时接近零。
-
抗扰性能 加入外界扰动后,控制系统仍能维持稳定,无人机姿态和位置能够迅速恢复到平衡状态。
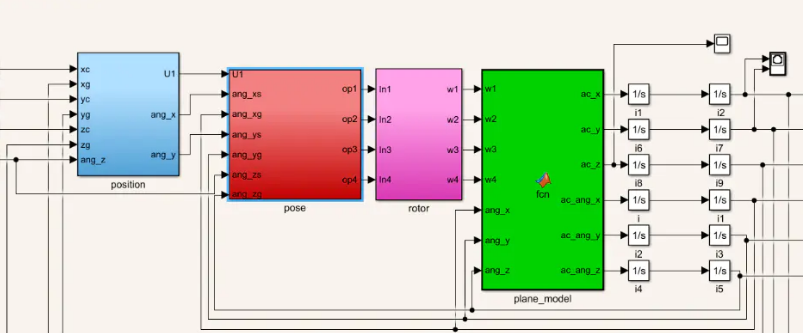
部分代码
% 初始化参数
Kp_pos = 1.2; Ki_pos = 0.5; Kd_pos = 0.8; % 位置控制器参数
Kp_att = 1.5; Ki_att = 0.7; Kd_att = 1.0; % 姿态控制器参数% 时间步长
Ts = 0.01;
time = 0:Ts:10;% 初始状态
pos_ref = [0; 0; -5]; % 期望位置
att_ref = [0; 0; 0]; % 期望姿态pos = [0; 0; 0];
att = [0; 0; 0];
error_int_pos = [0; 0; 0];
error_int_att = [0; 0; 0];for k = 1:length(time)% 计算位置误差error_pos = pos_ref - pos;error_int_pos = error_int_pos + error_pos * Ts;pos_cmd = Kp_pos * error_pos + Ki_pos * error_int_pos + Kd_pos * (error_pos / Ts);% 姿态控制error_att = att_ref - att;error_int_att = error_int_att + error_att * Ts;att_cmd = Kp_att * error_att + Ki_att * error_int_att + Kd_att * (error_att / Ts);% 更新无人机动态模型[pos, att] = quadcopter_dynamics(pos_cmd, att_cmd);
end% 动态模型
function [pos, att] = quadcopter_dynamics(pos_cmd, att_cmd)% 简化的动力学模型更新pos = pos + 0.1 * pos_cmd; % 更新位置att = att + 0.1 * att_cmd; % 更新姿态
end
参考文献
❝
Bouabdallah, S., Murrieri, P., & Siegwart, R. (2004). Design and Control of an Indoor Micro Quadrotor. IEEE International Conference on Robotics and Automation, 4393-4398.
Castillo, P., Lozano, R., & Dzul, A. (2005). Modelling and Control of Mini-Flying Machines. Springer Tracts in Advanced Robotics.
Hoffmann, G. M., Huang, H., & Waslander, S. L. (2008). Quadrotor Helicopter Flight Dynamics and Control: Theory and Experiment. Proceedings of the AIAA Guidance, Navigation, and Control Conference.
(文章内容仅供参考,具体效果以图片为准)