给你一个二叉树的根节点 root ， 检查它是否轴对称。

示例 1：

输入：root = [1,2,2,3,4,4,3]
输出：true

示例 2：

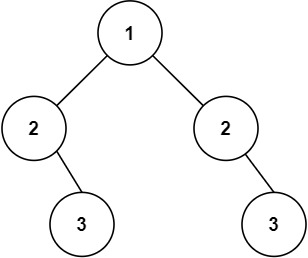
输入：root = [1,2,2,null,3,null,3]
输出：false

提示：

• 树中节点数目在范围 [1, 1000] 内
• -100 <= Node.val <= 100

进阶：你可以运用递归和迭代两种方法解决这个问题吗？

步骤1：分析问题性质

问题定义：

我们需要检查一个二叉树是否是轴对称的（即镜像对称）。

• 二叉树被称为轴对称，如果它的左子树是右子树的镜像。
• 输入：二叉树的根节点 root。
• 输出：布尔值，true 表示轴对称，false 表示不对称。

输入输出条件：

• 输入条件：
  • root 是一个二叉树的根节点，节点数目范围是 [1, 1000]。
  • 节点的值范围是 [-100, 100]。
• 输出条件：
  • 返回一个布尔值，true 或 false。

边界条件：

1. 空树：如果树为空（root == nullptr），它是对称的。
2. 只有一个节点：显然是对称的。
3. 不完全树：树中某些节点为 null，需要特殊处理。

---

步骤2：算法设计与分解

我们可以用 递归 和 迭代 两种方式检查二叉树是否对称。

递归方法

递归法本质上是一个深度优先搜索（DFS），比较两棵子树是否镜像对称。

• 对两棵子树 t1 和 t2：
  • 它们的值必须相等；
  • t1 的左子树和 t2 的右子树必须镜像；
  • t1 的右子树和 t2 的左子树必须镜像。
• 递归的基准条件：
  • 如果两棵子树都为空，返回 true。
  • 如果只有一棵子树为空，返回 false。
  • 如果两棵子树的值不相等，返回 false。

时间复杂度：O(n)，需要遍历每个节点一次。
空间复杂度：O(h)，递归调用栈的深度，h 是树的高度。

迭代方法

通过队列实现广度优先搜索（BFS）。

• 每次比较两个节点：
  • 如果它们的值不相等，返回 false。
  • 将它们的子节点按照对称顺序（t1.left 和 t2.right, t1.right 和 t2.left）加入队列。
• 如果队列为空且没有返回 false，说明树是对称的。

时间复杂度：O(n)，需要遍历每个节点一次。
空间复杂度：O(n)，队列中最多存储树的每一层节点。

---

步骤3：C++代码实现

递归法

迭代法

步骤4：解题启发

1. 递归与迭代的比较：

   • 递归代码更简洁，但需要注意栈溢出的风险，尤其是当树非常深时。
   • 迭代方法虽然稍显复杂，但更适合用于大规模树结构。

2. 树结构的对称性：

   • 检查树的对称性可以用于二叉树的多种特性验证，如镜像生成、对称剪枝等。

3. 边界条件的重要性：

   • 空树与单节点树的情况需要特别处理，以避免逻辑错误。

---

步骤5：实际应用分析

实际应用场景： 对称性检测在以下场景中非常重要：

1. 图像处理：

   • 在计算机视觉中，图像对称性检测可以用于模式识别、对称性补全。
   • 实现方式：将图像数据用树结构表示，然后检查镜像对称性。

2. 数据完整性验证：

   • 在文件系统、分布式存储中，可以使用对称性检查来验证数据块的完整性。

实际示例： 例如，医疗图像中的大脑扫描往往需要验证左右两侧的对称性以发现异常。

• 实现方式：将图像分成两部分，构建树状结构，使用上述算法检查两部分是否对称，从而检测异常区域。