给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

示例 1：

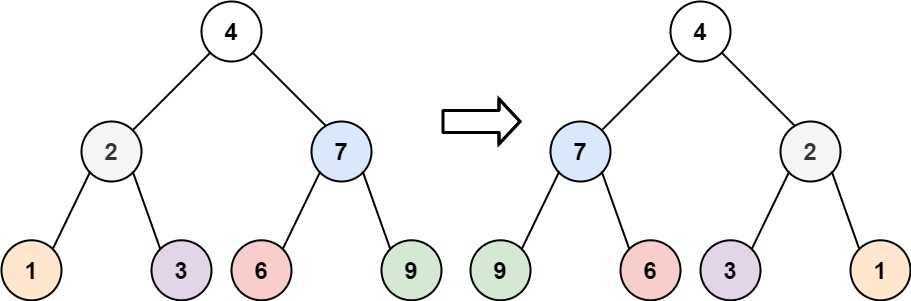
输入：root = [4,2,7,1,3,6,9]
输出：[4,7,2,9,6,3,1]

示例 2：

输入：root = [2,1,3]
输出：[2,3,1]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目范围在 [0, 100] 内
• -100 <= Node.val <= 100

步骤1：问题定义与分析

问题性质

该问题要求翻转一棵二叉树，翻转的定义是将二叉树的左右子树交换。最终返回翻转后的二叉树。

输入输出

1. 输入：
   • 一棵二叉树的根节点 root。
   • 树中节点数目范围在 [0, 100]。
   • 节点值范围在 [-100, 100]。
2. 输出：
   • 翻转后的二叉树的根节点。

边界条件

1. 空树：如果输入的树是空树（root == nullptr），直接返回空树。
2. 单节点树：如果树只有一个节点，无需翻转，直接返回原树。

---

步骤2：解题思路与算法设计

翻转二叉树的核心操作是将每个节点的左子树和右子树交换，可以采用递归或迭代的方式来实现。

递归法

1. 基本思路：
   • 从根节点开始，递归地对左右子树进行翻转。
   • 在每个节点，将其左右子树交换。
2. 递归终止条件：
   • 如果当前节点为 nullptr，直接返回。
3. 处理逻辑：
   • 递归处理当前节点的左子树和右子树。
   • 完成后，将左右子树交换。

迭代法

1. 基本思路：
   • 使用栈或队列进行广度优先搜索（BFS）或深度优先搜索（DFS）。
   • 对于每个访问的节点，交换其左右子树，并将其子节点加入栈或队列。
2. 适用场景：
   • 当树的层级过深，递归可能会导致栈溢出，迭代方法更为安全。

算法复杂度

1. 时间复杂度：O(n)
   • 每个节点访问一次，因此时间复杂度与节点数 n 成正比。
2. 空间复杂度：
   • 递归方法：O(h)，其中 h 为树的高度，递归栈的深度。
   • 迭代方法：O(w)，其中 w 为树的最大宽度，对应队列或栈的最大空间使用量。

---

步骤3：C++代码实现

步骤4：启发与优化

启发

1. 递归的优势：
   • 代码简洁，适合树状结构问题。
   • 通过递归自然地处理左右子树翻转，逻辑清晰。
2. 迭代的必要性：
   • 在深度较大的树中，为避免栈溢出，可以考虑使用迭代方法。
3. 时间与空间的权衡：
   • 对于二叉树翻转这类问题，递归和迭代的时间复杂度一致，选择方法取决于实际需求和树的规模。

优化潜力

1. 避免冗余操作：
   • 通过尾递归优化，可以减少递归调用的开销。
2. 并行处理：
   • 如果二叉树较大，可以利用多线程同时处理左右子树，进一步提升效率。

---

步骤5：实际生活中的应用

场景：图像处理中的镜像翻转

• 具体应用：在图像处理领域，许多操作需要将图像沿某个轴对称翻转。可以将图像像素点的分布用树结构表示，然后翻转该树。
• 实现方法：
  1. 将图像分块，使用树状结构存储每块像素的信息。
  2. 使用翻转二叉树的算法对每块图像进行左右交换。
  3. 合并翻转后的结果生成新的图像。
• 具体实例：某些图像编辑器或滤镜功能中，快速实现水平镜像处理。

这种算法还可以用于其他需要结构对称的场景，如数据重构、镜像存储和对称加密等。