Bellman_ford 队列优化算法(又名SPFA)
94. 城市间货物运输 I
思路
大家可以发现 Bellman_ford 算法每次松弛 都是对所有边进行松弛。
但真正有效的松弛,是基于已经计算过的节点在做的松弛。
给大家举一个例子:

本图中,对所有边进行松弛,真正有效的松弛,只有松弛 边(节点1->节点2) 和 边(节点1->节点3) 。
而松弛 边(节点4->节点6) ,边(节点5->节点3)等等 都是无效的操作,因为 节点4 和 节点 5 都是没有被计算过的节点。
所以 Bellman_ford 算法 每次都是对所有边进行松弛,其实是多做了一些无用功。
只需要对 上一次松弛的时候更新过的节点作为出发节点所连接的边 进行松弛就够了。
基于以上思路,如何记录 上次松弛的时候更新过的节点呢?
用队列来记录。(其实用栈也行,对元素顺序没有要求)
代码
#include<iostream>
#include<vector>
#include<queue>
#include<list>
#include<climits>
using namespace std;
struct Edge{//邻接表
int to;//邻接顶点
int val;//边的权值
Edge(int t,int w):to(t),val(w){}
};
int main()
{int n,m,p1,p2,val;//节点数、边数、边的两个节点和边的权重。cin>>n>>m;vector<list<Edge>>grid(n+1);//每个元素是一个链表 list<Edge>,用于存储图的邻接表。vector<bool>isInQueue(n+1);//用于标记每个节点是否已经在队列中,避免重复添加。for(int i=0;i<m;i++){cin>>p1>>p2>>val;grid[p1].push_back(Edge(p2,val));}int start=1;int end=n;vector<int>minDist(n+1,INT_MAX);minDist[start]=0;queue<int>que;//用于存储需要处理的节点。que.push(start);//SPFA算法核心while(!que.empty()){int node=que.front();que.pop();//获取并移除队列的前端节点 node。isInQueue[node]=false;//标记当前节点 node 已不在队列中。for(Edge edge:grid[node])//遍历当前节点 node 指向的所有邻接节点 edge{int from=node;//当前节点 node 作为出发点。int to=edge.to;//邻接节点 edge.to 作为到达点。int value=edge.val;if(minDist[to]>minDist[from]+value)//开始松弛{minDist[to]=minDist[from]+value;//如果通过当前节点 from 到达 to 的距离更短,则更新 minDist[to]if(isInQueue[to]==false)//如果到达点 to 不在队列中,则将其加入队列,并标记为已在队列中。{que.push(to);//将到达点 to 加入队列。isInQueue[to]=true;//标记到达点 to 已在队列中。}}}}if(minDist[end]==INT_MAX)cout<<"unconnected"<<endl;elsecout<<minDist[end]<<endl;}模拟过程
假设输入如下:
4 4 1 2 1 1 3 4 2 3 1 3 4 1
首先读取
n=4和m=4,初始化邻接表grid。读取边并填充邻接表:
- 边
(1, 2, 1),grid[1].push_back(Edge(2, 1))- 边
(1, 3, 4),grid[1].push_back(Edge(3, 4))- 边
(2, 3, 1),grid[2].push_back(Edge(3, 1))- 边
(3, 4, 1),grid[3].push_back(Edge(4, 1))初始化
minDist和isInQueue。初始化队列,将起始点1加入队列。
运行 SPFA 算法:
- 第一次迭代:从队列中取出节点1,更新
minDist为[0, 1, 4, INT_MAX],并将节点2和3加入队列。- 第二次迭代:从队列中取出节点2,更新
minDist为[0, 1, 2, INT_MAX],并将节点3加入队列。- 第三次迭代:从队列中取出节点3,更新
minDist为[0, 1, 2, 3],并将节点4加入队列。- 第四次迭代:从队列中取出节点4,
minDist保持不变。最终输出:
3
bellman_ford之判断负权回路
95. 城市间货物运输 II
题目描述
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
然而,在评估从城市 1 到城市 n 的所有可能路径中综合政府补贴后的最低运输成本时,存在一种情况:图中可能出现负权回路。负权回路是指一系列道路的总权值为负,这样的回路使得通过反复经过回路中的道路,理论上可以无限地减少总成本或无限地增加总收益。为了避免货物运输商采用负权回路这种情况无限的赚取政府补贴,算法还需检测这种特殊情况。
请找出从城市 1 到城市 n 的所有可能路径中,综合政府补贴后的最低运输成本。同时能够检测并适当处理负权回路的存在。
城市 1 到城市 n 之间可能会出现没有路径的情况
输入描述
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v。
输出描述
如果没有发现负权回路,则输出一个整数,表示从城市
1到城市n的最低运输成本(包括政府补贴)。如果该整数是负数,则表示实现了盈利。如果发现了负权回路的存在,则输出 "circle"。如果从城市 1 无法到达城市 n,则输出 "unconnected"。输入示例
4 4 1 2 -1 2 3 1 3 1 -1 3 4 1输出示例
circle提示信息
路径中存在负权回路,从 1 -> 2 -> 3 -> 1,总权值为 -1,理论上货物运输商可以在该回路无限循环赚取政府补贴,所以输出 "circle" 表示已经检测出了该种情况。
数据范围:
1 <= n <= 1000;
1 <= m <= 10000;-100 <= v <= 100;
思路
本题是要我们判断 负权回路,也就是图中出现环且环上的边总权值为负数。
如果在这样的图中求最短路的话, 就会在这个环里无限循环 (也是负数+负数 只会越来越小),无法求出最短路径。
所以对于 在有负权值的图中求最短路,都需要先看看这个图里有没有负权回路。
如果在负权回路多绕两圈,三圈,无穷圈,那么我们的总成本就会无限小, 如果要求最小成本的话,你会发现本题就无解了。
在 bellman_ford 算法中,松弛 n-1 次所有的边 就可以求得 起点到任何节点的最短路径,松弛 n 次以上,minDist数组(记录起到到其他节点的最短距离)中的结果也不会有改变 。
而本题有负权回路的情况下,一直都会有更短的最短路,所以 松弛 第n次,minDist数组 也会发生改变。
那么解决本题的 核心思路,就是在 kama94.城市间货物运输I 的基础上,再多松弛一次,看minDist数组 是否发生变化。变化了就代表有负权回路。代码和 kama94.城市间货物运输I 基本是一样的。
代码
//和上题代码基本一致,就是需要多松弛一次
#include<iostream>
#include<vector>
#include<list>
#include<climits>
using namespace std;
int main()
{int n,m,p1,p2,val;cin>>n>>m;vector<vector<int>>grid;//用于存储所有的边,每条边用一个包含三个整数的向量表示。for(int i=0;i<m;i++){cin>>p1>>p2>>val;grid.push_back({p1,p2,val});}int start=1;int end=n;vector<int>minDist(n+1,INT_MAX);minDist[start]=0;//Bellman-Ford算法bool flag=false;//!!用于标记是否存在负权回路。for(int i=1;i<=n;i++) 这里我们松弛n次,最后一次判断负权回路{for(vector<int>&side:grid){int from=side[0];//起点int to=side[1];//到达点int price=side[2];//边的权值if(i<n)//前 n-1 次松弛操作,更新最短路径。{//如果出发点的最短距离不是 INT_MAX 且通过当前边到达点的最短距离可以更新,则进行更新。if(minDist[from]!=INT_MAX&&minDist[to]>minDist[from]+price)minDist[to]=minDist[from]+price;}else//第 n 次松弛操作,用于检测负权回路。{//如果出发点的最短距离不是 INT_MAX 且通过当前边到达点的最短距离可以更新,则标记 flag 为 true。if(minDist[from]!=INT_MAX&&minDist[to]>minDist[from]+price)flag=true;}}}if(flag)cout<<"circle"<<endl;else if(minDist[end]==INT_MAX)cout<<"unconnected"<<endl;elsecout<<minDist[end]<<endl;}模拟运行结果
假设输入如下:
4 5 1 2 1 1 3 4 2 3 1 3 4 1 4 1 -5
首先读取
n=4和m=5,初始化边的存储grid。读取边并存储在
grid中:
- 边
(1, 2, 1),grid.push_back({1, 2, 1})- 边
(1, 3, 4),grid.push_back({1, 3, 4})- 边
(2, 3, 1),grid.push_back({2, 3, 1})- 边
(3, 4, 1),grid.push_back({3, 4, 1})- 边
(4, 1, -5),grid.push_back({4, 1, -5})初始化
minDist,设置minDist[start] = 0。运行 Bellman-Ford 算法:
- 第一次松弛:
- 处理边
(1, 2, 1),更新minDist[2] = 1。- 处理边
(1, 3, 4),更新minDist[3] = 4。- 处理边
(2, 3, 1),更新minDist[3] = 2。- 处理边
(3, 4, 1),更新minDist[4] = 3。- 处理边
(4, 1, -5),更新minDist[1] = -2。- 第二次松弛:
- 处理边
(1, 2, 1),更新minDist[2] = -1。- 处理边
(1, 3, 4),更新minDist[3] = 3。- 处理边
(2, 3, 1),更新minDist[3] = -1。- 处理边
(3, 4, 1),更新minDist[4] = 0。- 处理边
(4, 1, -5),更新minDist[1] = -5。- 第三次松弛:
- 处理边
(1, 2, 1),更新minDist[2] = -4。- 处理边
(1, 3, 4),更新minDist[3] = -1。- 处理边
(2, 3, 1),更新minDist[3] = -4。- 处理边
(3, 4, 1),更新minDist[4] = -3。- 处理边
(4, 1, -5),更新minDist[1] = -8。- 第四次松弛(检测负权回路):
- 处理边
(1, 2, 1),更新minDist[2] = -7。- 处理边
(1, 3, 4),更新minDist[3] = -4。- 处理边
(2, 3, 1),更新minDist[3] = -7。- 处理边
(3, 4, 1),更新minDist[4] = -6。- 处理边
(4, 1, -5),更新minDist[1] = -11。- 发现
minDist[1]在第n次松弛后仍然可以更新,说明存在负权回路。最终输出:
circle
bellman_ford之单源有限最短路
96. 城市间货物运输 III
题目描述
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
请计算在最多经过 k 个城市的条件下,从城市 src 到城市 dst 的最低运输成本。
输入描述
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v。
最后一行包含三个正整数,src、dst、和 k,src 和 dst 为城市编号,从 src 到 dst 经过的城市数量限制。
输出描述
输出一个整数,表示从城市 src 到城市 dst 的最低运输成本,如果无法在给定经过城市数量限制下找到从 src 到 dst 的路径,则输出 "unreachable",表示不存在符合条件的运输方案。
输入示例
6 7 1 2 1 2 4 -3 2 5 2 1 3 5 3 5 1 4 6 4 5 6 -2 2 6 1输出示例
0提示信息
从 2 -> 5 -> 6 中转一站,运输成本为 0。
1 <= n <= 1000;
1 <= m <= 10000;
-100 <= v <= 100;
思路
本题是最多经过 k 个城市的条件下,而不是一定经过k个城市,也可以经过的城市数量比k小,但要最短的路径。
本题是最多经过 k 个城市, 那么是 k + 1条边相连的节点。 这里可能有录友想不懂为什么是k + 1,来看这个图:
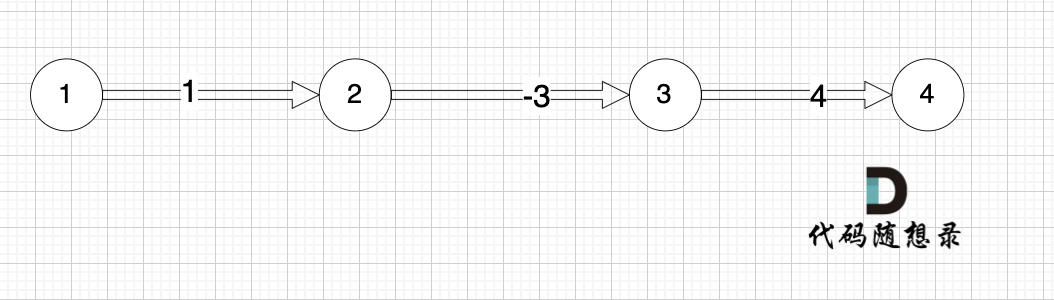
图中,节点1 最多已经经过2个节点 到达节点4,那么中间是有多少条边呢,是 3 条边对吧。
所以本题就是求:起点最多经过k + 1 条边到达终点的最短距离。
对所有边松弛一次,相当于计算 起点到达 与起点一条边相连的节点 的最短距离,那么对所有边松弛 k + 1次,就是求 起点到达 与起点k + 1条边相连的节点的 最短距离。
注意本题也是有负权回路的
在每次计算 minDist 时候,要基于 对所有边上一次松弛的 minDist 数值才行,所以我们要记录上一次松弛的minDist。
代码
这个版本的算法通过在每次松弛操作中使用一个临时的副本 minDist_copy 来避免在同一次松弛中多次更新同一个节点的距离,从而确保每次松弛操作都是基于上一次的结果进行的。
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
int main()
{int n,m,p1,p2,val,src,dst,k;//节点数,边数,边的权重,起始点,目标点,最大中转次数cin>>n>>m;vector<vector<int>>grid;//用于存储所有的边,每条边用一个包含三个整数的向量表示。for(int i=0;i<m;i++)//初始化边的存储{cin>>p1>>p2>>val;grid.push_back({p1,p2,val});}cin>>src>>dst>>k;vector<int>minDist(n+1,INT_MAX);minDist[src]=0;//因为距离自身的距离等于0vector<int>minDist_copy(n+1);//用来记录上一次遍历的结果for(int i=1;i<=k+1;i++)//松弛k+1条边的次数,其中k是最大中转次数{minDist_copy=minDist;//获取上一次计算的结果for(vector<int>&side:grid){int from=side[0];int to=side[1];int price=side[2];//如果出发点的最短距离不是 INT_MAX 且通过当前边到达点的最短距离可以更新,则进行更新。if(minDist_copy[from]!=INT_MAX&&minDist[to]>minDist_copy[from]+price){minDist[to]=minDist_copy[from]+price;}}}if(minDist[dst]==INT_MAX)cout<<"unreachable"<<endl;//不能到达终点else cout<<minDist[dst]<<endl;//到达终点最短路径}模拟运行结果
假设输入如下:
4 4 1 2 1 1 3 4 2 3 1 3 4 1 1 4 2
首先读取
n=4和m=4,初始化边的存储grid。读取边并存储在
grid中:
- 边
(1, 2, 1),grid.push_back({1, 2, 1})- 边
(1, 3, 4),grid.push_back({1, 3, 4})- 边
(2, 3, 1),grid.push_back({2, 3, 1})- 边
(3, 4, 1),grid.push_back({3, 4, 1})读取起始点
src=1、目标点dst=4和最大中转次数k=2。初始化
minDist,设置minDist[src] = 0。运行改进的 Bellman-Ford 算法:
- 第一次松弛:
- 处理边
(1, 2, 1),更新minDist[2] = 1。- 处理边
(1, 3, 4),更新minDist[3] = 4。- 处理边
(2, 3, 1),更新minDist[3] = 2。- 处理边
(3, 4, 1),更新minDist[4] = 3。- 第二次松弛:
- 处理边
(1, 2, 1),minDist[2]保持不变。- 处理边
(1, 3, 4),minDist[3]保持不变。- 处理边
(2, 3, 1),minDist[3]保持不变。- 处理边
(3, 4, 1),minDist[4]保持不变。- 第三次松弛:
- 处理边
(1, 2, 1),minDist[2]保持不变。- 处理边
(1, 3, 4),minDist[3]保持不变。- 处理边
(2, 3, 1),minDist[3]保持不变。- 处理边
(3, 4, 1),minDist[4]保持不变。最终输出:
3



















