Schnorr 和 BLS 算法详解

Schnorr 签名和 BLS 签名在区块链技术中都有着重要的应用。它们各自具备独特的优势，使其在不同的区块链应用场景中得到广泛使用。

Schnorr签名算法

Schnorr签名算法是一种基于离散对数问题的数字签名算法， 由德国密码学家 克劳斯·施诺尔 （Claus-Peter Schnorr）于1989年提出。Schnorr签名算法以其 签名生成和验证的高效性和简洁性 著称，是许多现代密码系统的重要组成部分。以下是Schnorr签名算法的基本工作原理和过程：

1.1 算法参数

选择一个大素数 𝑝：确保 𝑝 足够大以保证安全性。
选择一个素数 𝑞，𝑞 是 𝑝−1 的一个因子，通常 𝑞 较小。
选择一个生成元 𝑔, 𝑔 是 𝑍_𝑝^∗ (整数模 𝑝p 的乘法群）的生成元,满足

𝑔𝑞≡1(𝑚𝑜𝑑𝑝)。

1.2 密钥生成

私钥 𝑥：选择一个随机的私钥 𝑥 满足 0<𝑥<𝑞。
公钥 𝑦：计算公钥 𝑦，满足

𝑦≡𝑔𝑥(𝑚𝑜𝑑𝑝)

1.3 签名生成

选择一个随机数 𝑘：选择一个随机数 𝑘k 满足 0<𝑘<𝑞。
计算 𝑟：计算 𝑟≡𝑔𝑘(𝑚𝑜𝑑𝑝)
计算哈希值 𝑒：将消息 𝑚 和 𝑟 结合，计算哈希值 𝑒=𝐻(𝑚,𝑟) 其中 𝐻 是一个安全的哈希函数。
计算签名 𝑠：计算 𝑠≡(𝑘+𝑥𝑒)(mod𝑞)

生成的签名为 (𝑒,𝑠)。

1.4 签名验证

验证 𝑟：通过公钥 𝑦y 和签名 (𝑒,𝑠) 计算 𝑟′： 𝑟′≡𝑔𝑠⋅𝑦−𝑒(𝑚𝑜𝑑𝑝)
计算哈希值 𝑒′：将消息 𝑚m 和计算得到的 𝑟′ 结合，计算哈希值 𝑒′=𝐻(𝑚,𝑟′)。
验证签名：如果 𝑒′=𝑒，则签名有效；否则签名无效。

1.5 优点

高效性：相比于其它签名算法，Schnorr签名在计算上更加高效，特别是在签名生成和验证过程中。
短签名：Schnorr签名长度较短，有助于节省带宽和存储空间。
安全性：基于离散对数问题的安全性，难以被破解。

1.6 应用

Schnorr签名广泛应用于区块链和加密货币领域，如比特币的Taproot升级中使用了基于Schnorr签名的聚合签名技术。此外，许多密码协议和标准也采用了Schnorr签名算法。

总之，Schnorr签名算法以其高效和安全的特点，成为了现代密码学中的一个重要工具，尤其在对资源要求较高的应用场景中具有显著优势。

基于有限单群的Schnorr 多重数字签名算法

基于有限单群的 Schnorr 签名算法是一种扩展和改进的 Schnorr 签名方案，其核心思想仍然依赖于 离散对数问题 ，但引入了 有限单群（finite simple group） 的概念。这种改进可以在某些方面提供额外的安全性和效率。

2.1 什么是有限单群

有限单群是仅有一个非平凡正规子群（即它自身）的群 。这些群在代数结构上具有较高的对称性和复杂性，因此在密码学中应用能够增加某些攻击的难度。

2.2 基于有限单群的 Schnorr 签名算法

2.2.1 算法参数

选择有限单群 𝐺：选择一个有限单群 𝐺 及其阶 𝑛
选择生成元 𝑔: 选择 𝐺 的一个生成元 𝑔。

2.2.2 密钥生成

私钥 𝑥 选择一个随机的私钥 𝑥 满足 0<𝑥<n< span="">
公钥 y, 计算公钥 𝑦=𝑔^𝑥

2.2.3 签名生成

选择一个随机数 𝑘, 𝑘 满足 0 < k < n
计算 r，r = g^k
计算哈希值 𝑒, 将消息 𝑚 和 𝑟 结合，计算哈希值 𝑒=𝐻(𝑚,𝑟), 其中 𝐻 是一个安全的哈希函数
计算签名 𝑠, 𝑠≡(𝑘+𝑥𝑒)(mod𝑛)

生成的签名为 (𝑒, 𝑠)

2.2.4 签名验证

验证 𝑟, 通过公钥 𝑦 和签名 (𝑒,𝑠) 计算 𝑟′, 𝑟≡𝑔^𝑠.𝑦^{−𝑒}
计算哈希值 𝑒′：将消息 𝑚 和计算得到的 𝑟′结合，计算哈希值 𝑒′=𝐻(𝑚,𝑟)。
验证签名：如果 𝑒′=𝑒 则签名有效；否则签名无效。

2.2.5 优点

高安全性：由于有限单群的复杂结构，攻击者更难破解基于这些群的签名。
高效性：算法保持了Schnorr签名的高效特点。
较短的签名长度：签名长度较短，有助于节省带宽和存储空间。

2.2.6 应用

基于有限单群的 Schnorr 签名算法可以用于需要高安全性和高效性的场合，如加密货币、区块链技术和其他需要数字签名的应用领域。

总的来说，基于有限单群的 Schnorr 签名算法通过引入有限单群的结构，增强了算法的安全性，同时保持了原始 Schnorr 签名的效率和简洁性。

基于有限单群的 Schnorr 多重数字签名算法

基于有限单群的 Schnorr 多重数字签名算法是对传统 Schnorr 签名算法的扩展， 使其能够支持多个签名者共同生成一个联合签名。这种方法在区块链和其他分布式系统中具有重要应用，特别是在提高效率和减少数据传输量方面。

3.1 多重签名算法的基本思想

多重签名算法允许多个参与者共同生成一个签名，该签名可以由任何一组验证者进行验证。具体来说，基于有限单群的 Schnorr 多重签名算法使用了有限单群的性质，以增强安全性和性能。

3.2 基于有限单群的 Schnorr 多重数字签名算法

3.2.1.算法参数

选择有限单群 𝐺：选择一个有限单群 𝐺 及其阶 𝑛
选择生成元 𝑔: 选择 𝐺 的一个生成元 𝑔。

3.2.2.密钥生成

每个签名者 𝑖(共有 𝑡个签名者）生成自己的密钥对：

私钥 𝑥_𝑖 选择一个随机的私钥 𝑥𝑖 满足 0<𝑥_𝑖<𝑛
公钥 𝑦_𝑖, 计算公钥 𝑦_𝑖=𝑔_𝑖^𝑥

联合公钥 ( y ) 为各个签名者公钥的乘积：

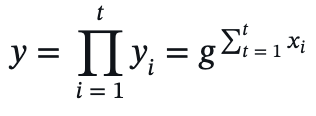
3.2.3. 签名生成

选择随机数 𝑘𝑖：每个签名者 𝑖 随机选择一个 ( k_i ) 满足 0<𝑘_𝑖<𝑛。
计算 𝑟_𝑖：每个签名者计算 𝑟_𝑖=𝑔^𝑘_𝑖。
广播 𝑟_𝑖：各个签名者相互广播 𝑟_𝑖。
计算 𝑟：汇总所有签名者的 𝑟_𝑖计算出联合值 𝑟：

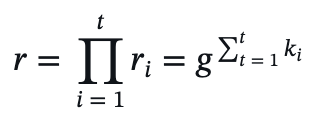
计算哈希值 e：将消息 m 和联合值 r 结合，计算哈希值 e = H(m, r)。
计算部分签名 𝑠𝑖：每个签名者计算部分签名 𝑠𝑖=𝑘𝑖+𝑥𝑖⋅𝑒𝑚𝑜𝑑𝑛
汇总部分签名 𝑠：所有签名者将他们的部分签名相加得到联合签名 𝑠：

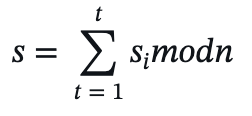
生成的联合签名为 (𝑒,𝑠)。

3.2.4.签名验证

验证 r：通过联合公钥 y 和联合签名 (e, s) 计算 r'

𝑟′=𝑔𝑠⋅𝑦−𝑒

计算哈希值 e'：将消息 m 和计算得到的 r' 结合，计算哈希值）𝑒′=𝐻(𝑚,𝑟′）。
验证签名：如果 e' = e，则签名有效；否则签名无效。

3.2.5.优点

提高安全性：基于有限单群的结构增加了破解难度。
高效性：联合签名减少了签名长度和通信开销。
灵活性：支持多方共同签名，提高了应用场景的灵活性和可扩展性。

3.2.6.应用

这种多重签名算法在分布式系统、区块链技术和需要多方共同认证的应用中非常有用，例如多重签名钱包、分布式密钥管理和共识协议等。

总的来说，基于有限单群的 Schnorr 多重数字签名算法通过结合有限单群的复杂结构和多重签名机制，提供了强大的安全性和高效性，适用于现代分布式系统和密码学应用。

BLS 算法

BLS (Boneh-Lynn-Shacham) 签名算法是一种基于双线性配对（bilinear pairing）和椭圆曲线密码学的数字签名算法， 由Dan Boneh, Ben Lynn, 和 Hovav Shacham在2001年提出。BLS签名以其简洁、短签名和强安全性著称，被广泛应用于区块链和其他分布式系统中。

4.1 基本原理

BLS签名算法基于以下数学结构和问题：

双线性配对

给定两个椭圆曲线群 𝐺_1 和 𝐺_2 以及一个目标群 𝐺_𝑇，存在一个双线性映射 𝑒:𝐺_1×𝐺_2→𝐺_𝑇 满足：

双线性性：e(aP, bQ) = e(P, Q)^{ab} 对所有 𝑃∈𝐺_1, 𝑄∈𝐺_2 和 𝑎,𝑏∈𝑍_𝑝。
非退化性：如果 𝑃≠𝑂 且，则𝑄≠𝑂)，则(𝑒(𝑃,𝑄)≠1。
有效性：计算 𝑒(𝑃,𝑄) 在有限时间内是可行的。

4.2 算法步骤

系统参数生成

选择一个大素数 𝑝。
选择椭圆曲线 𝐸 定义在有限域 𝐹𝑝 上。
选择群 𝐺1 的生成元 𝑃、G_2 的生成元 𝑄 和目标群 𝐺_𝑇 的生成元 𝑒(𝑃,𝑄)。
定义双线性映射 𝑒:𝐺_1×𝐺_2→𝐺_𝑇。

密钥生成

随机选择私钥 𝑥∈𝑍_𝑝。
计算对应的公钥 𝑝𝑘=𝑠𝑘⋅𝑃，其中 𝑃 是 𝐺1中的一个生成元。。

签名生成

给定消息 𝑚 和私钥 𝑠𝑘。
计算消息的哈希值 𝐻(𝑚)，其中 𝐻 是一个哈希函数，将消息映射到群 𝐺_1 中。
计算签名 𝜎=𝑠𝑘⋅𝐻(𝑚)。

签名验证

给定消息 𝑚、签名 𝜎 和公钥 𝑝𝑘。
计算消息的哈希值 𝐻(𝑚)。
验证 𝑒(𝜎,𝑃)=𝑒(𝐻(𝑚),𝑝𝑘)，其中 𝑒 是双线性对映射。

4.3 特点和应用

简洁性：BLS签名非常简洁，签名的大小固定且较小，只有一个群元素。
效率：签名生成和验证的计算量相对较小，尤其是在签名长度较短的情况下。
聚合签名：BLS签名具有天然的签名聚合（aggregate signature）特性，多个签名可以被聚合成一个签名，从而减少存储和传输的开销。这在区块链和分布式系统中尤为有用。
多重签名：BLS也支持多重签名（multi-signature），多个用户可以共同签署同一消息，生成一个联合签名。

4.4 应用领域

BLS签名由于其高效性和灵活性，在许多领域中得到了广泛应用，特别是在区块链技术和分布式系统中，如Ethereum 2.0、Zcash、Algorand等。

4.5 总结

BLS签名算法通过使用双线性对，实现了高效且简洁的签名方案，具有签名聚合和多重签名等重要特性，使其在现代密码学和区块链技术中具有重要的应用价值。

4.6 go 代码实现

package mainimport ("crypto/rand""fmt""github.com/kilic/bls12-381""golang.org/x/crypto/blake2b"
)// GenerateKeyPair 生成私钥和公钥
func GenerateKeyPair() (*bls12381.Scalar, *bls12381.PointG1) {sk := bls12381.NewFr()sk.Rand(rand.Reader)pk := bls12381.NewG1().ScalarBaseMult(sk)return sk, pk
}// HashToG2 将消息哈希到G2
func HashToG2(msg []byte) *bls12381.PointG2 {hash := blake2b.Sum256(msg)return bls12381.NewG2().HashToCurve(hash[:])
}// Sign 生成消息的签名
func Sign(sk *bls12381.Scalar, msg []byte) *bls12381.PointG2 {hashPoint := HashToG2(msg)signature := bls12381.NewG2().ScalarMult(hashPoint, sk)return signature
}// Verify 验证签名
func Verify(pk *bls12381.PointG1, msg []byte, signature *bls12381.PointG2) bool {hashPoint := HashToG2(msg)engine := bls12381.NewEngine()engine.AddPair(pk, hashPoint)pairingLeft := engine.Result()engine.Reset()engine.AddPair(bls12381.NewG1().One(), signature)pairingRight := engine.Result()return pairingLeft.Equal(pairingRight)
}func main() {// 生成密钥对sk, pk := GenerateKeyPair()// 要签名的消息msg := []byte("Hello, BLS!")// 生成签名signature := Sign(sk, msg)// 验证签名isValid := Verify(pk, msg, signature)fmt.Printf("签名有效: %v\n", isValid)
}

更多相关信息，，https://t.me/gtokentool